
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжённость поля точечного электрического заряда:Содержание книги
Поиск на нашем сайте
Вопрос №1 Электрический заряд. Дискретность электрического заряда. Элементарный заряд. Закон сохранения электрического заряда. Опыт Милликэна. Закон Кулона. Система единиц. Диэлектрическая постоянная. Линейная, поверхностная и объемная плотность зарядов. Электрический заряд – количественная мера действия степени электризации тел. Элементарный заряд - минимальная порция электрического заряда (e=1.6-19), заряд элементарной частицы (электрон, протон, нейтрон) Электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е. ЗСЭЗ: алгебраическая сумма эл. зарядов любой замкнутой системы не изменяется. Опыт Милликена: (1909) Между пластинами подавалось напряжение и, с помощью пульверизатора, капельки масла, в микроскоп велось наблюдение за установлением равновесия. Нашёл элементарный заряд. Закон Кулона: (1785) Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Точечный заряд - Заряженное тело, размерами которого можно пренебречь по сравнению с расстоянием до других тел.
Также для з.Кулона справедлив принцип суперпозиции: Опытным путём установлено, что взаимодействие двух электрических зарядов не зависит от наличия других зарядов. Диэлектрическая постоянная: Линейная плотность заряда: Поверхностная плотность заряда: Объёмная плотность заряда: Вопрос №2 Электрическое поле, его характеристики. Напряженность поля (точечного заряда и системы зарядов). Вектор электрического смещения. Графическое изображение электрических полей Эл. поле – это пространство, окруж-щее заряж. тела, в кажд. точке этого пространства сопоставлено какое-то значение физ. величины. Характеристики поля: напряжённость электрического поля Е, потенциал Ф, вектор смещения электрического поля D. Напряжённость поля: векторная физическая величина, равная отношению силы, действующей на заряд, к величине этого заряда. E=F/q.
Напряжённость поля точечного электрического заряда:
Вопрос №3 Работа перемещения электрического заряда в электрическом поле. Теорема о циркуляции вектора напряженности электрического поля. Потенциал электрического поля. Разность потенциалов. Эквипотенциальные поверхности. Потенциал поля точечного заряда и системы зарядов.
Кулоновская сила консервативна, а электростатическое поле - потенциально. Работа сил консервативного поля – убыль потенциальной энергии.
Потенциал: скал. физ. велич., равная потенц. эн., которой обладает ед. пол. заряд, помещ. в данную точку. (Wп/qпр) Потенциал поля точечного заряда: Потенциал поля системы зарядов: Wn=φq A=W1-W2 =q(φ1 – φ2) A=qφ (если заряд из точки с потенциалом φ удаляется на бесконечность)=> Потенциал: численно равен работе, которую совершают силы поля над единичным полож. зарядом при удалении его из данной точки на бесконечность.
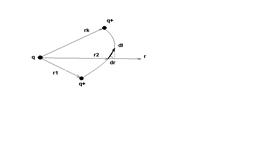
Теорема о циркуляции вектора напряжённости (признак потенциальности поля): циркуляция вектора Е равна нулю. Эквипотенциальные поверхности: воображаемые пов-ти, все точки которых имеют одинаковый потенциал. Уравнение такой пл-ти: φ(x,y,z)=Const Вектор Е в каждой точке направлен по нормали к эквипот. пов-ти. Линии напряжённости в каждой точке ортогональны к эквипот. пов-тям. Эквипот. пов-ть можно провести через любую точку поля => по густоте эквипот. пов-тей можно судить о величине напряжённости поля. Билет №4 Билет №5 Принцип суперпозиции Эл. Полей. Расчет поля (напряженности и потенциала) заряженной нити, кольца Принцип суперпозиции эл. полей: Напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов в отдельности.
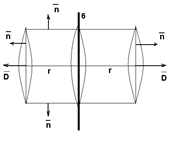
Билет №7 Билет №8 Применение теоремы Остроградского-Гаусса для расчета Эл. Полей (напряженности и потенциала) бесконечной заряженной плоскости, нескольких бесконечных заряженных плоскостей, бесконечной нити, бесконечного заряженного шара и сферы, цилиндра. Поле беск. заряж. плоскости
q=σS 2DS=σS D=σ/2 => поле однородное
Напряжённость поля бесконечного цилиндра: Билет №9 Диэлектрики. Типы диэлектриков. Полярные и неполярные молекулы в Эл. Поле (однородном и неоднородном). Электронная и ориентационная поляризация диэлектриков. Вектор поляризации. Диэлектрическая восприимчивость вещества и ее зависимость от температуры. Молекулы диэлектриков – диполи. Молекулы: 1)Неполярные (в отсутствии эл. поля Pe=0) 2)Полярные (в отсутсвии эл. поля Pe!=0) Полярные молекулы в электрическом поле: диполи в Эл. поле стремятся сориентироваться так, что Pe||E. Но есть хаотическое тепловое движение => диполи только стремятся, ориентация преимущественная.(ориентационная поляриз.) Неполярные молекулы в электрическом поле: В поле деформируются Вектор поляризации: Количественная характеристика поляризации диэлектриков – вектор поляризации – физическая вел-на, численно равная суммарному Эл моменту молекул в единице объёма диэлектрика. Вектор поляризации у неполярных диэлектриков: α n = 96 – диэлетрическая восприимчивость вещества(«капа») P =96 ε0E Билет № 10 Билет №11 Билет №12 Билет №13 Билет 14 Билет №15 Билет №16 Постоянный Эл. Ток, его характеристики (сила тока, плотность тока) и условия существования. Сторонние силы. ЭДС сторонних сил. Сопротивление проводников. Проводники, полупроводники, изоляторы и сверхпроводники. Законы Ома и Джоуля-Ленца в интегральной и дифференциальной форме Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Е свободные электрические заряды перемещаются: положительные — по полю, отрицательные — против поля, т. е. в проводнике возникает электрический ток, называемый током проводимости. Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заряженного макроскопического тела, то возникает так называемый конвекционный ток. Для возникновения и существования электрического тока необходимо, с одной стороны, наличие свободных носителей тока — заряженных частиц, способных перемещаться упорядоченно, а с другой — наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. За направление тока условно принимают направление движения положительных зарядов. Количественной мерой электрического тока служит сила тока I — скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени: I=dq / dt. Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока I=Q/t, где Q — электрический заряд, проходящий за время t через поперечное сечение проводника. Единица силы тока — ампер (А). Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока: j=dI/dS Плотность тока — вектор, ориентированный по направлению тока, т. е. направление вектора j совпадает с направлением упорядоченного движения положительных зарядов. Единица плотности тока — ампер на метр в квадрате (А/м2). Сила тока сквозь произвольную поверхность S определяется как поток вектора j,т. е. I= Сторонние силы. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними. Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ротора генератора и т. п. Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (э. д. с.), действующей в цепи Сторонняя сила F, действующая на заряд Qo. может быть выражена как где Е — напряженность поля сторонних сил. Работа же сторонних сил по перемещению заряда Qo на замкнутом участке цепи равна Сопротивление проводников Немецкий физик Г. Ом экспериментально установил, что сила тока I, текущего проводнику, пропорциональна напряжению U на концах проводника: I=U/R где R — электрическое сопротивление проводника. Это уравнение выражает закон Ома для участка цепи (не содержащего источника тока): сала тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Единица сопротивления — ом (Ом). 1Ом — сопротивление такого проводника, в котором при напряжении 1В течет постоянный ток 1 А. Величина G=1/R называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине / и обратно пропорционально площади его поперечного сечения S: R = pl / S где р — коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением. Единица удельного электрического сопротивления — Ом метр (Ом • м). Наименьшим удельным сопротивлением обладают серебро (1,6 -10-8 Ом-м) и медь (1,7-10-8 Ом-м). Билет №17 Классическая электронная теория электропроводности металлов и ее опытные обоснования. Вывод законов Ома и Джоуля-Ленца из электронных представлений. Закон Видемана-Франца. Затруднения классической теории электропроводности металлов. 1) Носителями тока в металлах являются свободные электроны (Первый из таких опытов, подтверждающих то, что электрон – носитель заряда—опыт Рикке, в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (Сu, Аl, Сu) одинакового радиуса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (3,5-10+6 Кл), никаких, даже микроскопических, следов переноса не обнаружилось. Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металле осуществляется частицами, которые являются общими для всех металлов.) 2) Свободные электроны ведут себя как идеальный электронный газ. (По теории Друде — Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории, можно найти среднюю скорость теплового движения электронов
3) При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость <V> упорядоченного движения электронов можно оценить согласно формуле для плотности тока: j= ne<V>. <V><<<U>, т.е. даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях результирующую скорость (<V>+<U>) можно заменять скоростью теплового движения <U>. Закон Ома. Пусть в металлическом проводнике существует электрическое поле. Напряженностью E= const. Co стороны поля заряд е испытывает действие силы F = eE и приобретает ускорение a=F/m=eE/m. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
где <t> — среднее время между двумя последовательными соударениями с ионами решетки. Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона
Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время <t> свободного пробега определяется средней длиной свободного пробега <l> и средней скоростью движения электронов относительно кристаллической решетки проводника, равной <U>+<V> (<U>— средняя скорость теплового движения электронов). <V><<<U>, поэтому <t>=<l>/<U> <V>=eE<l>/(2m<U>) Плотность тока в металлическом проводнике,
откуда видно, что плотность тока пропорциональна напряженности поля, т. е. получи ли закон Ома в дифференциальной форме.
Закон Джоуля-Ленца К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию.
При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание. За единицу времени электрон испытывает с узлами решетки в среднем <z> столкновений: <z>=<U>/<l> Если п — концентрация электронов, то в единицу времени происходит n < z > столкновений и решетке передается энергия w=n<z><E>, которая идет на нагревание проводника. Таким образом энергию, передаваемую решетке в единице объема проводника за единицу времени Величина w является удельной тепловой мощностью тока. Коэффициент пропорциональности между w в Закон Видемана-Франца Видеманом и Францем экспериментально установлен закон, согласно
Элементарная классическая теория электропроводности металлов позволила найти значение Рассмотрим некоторые из них. Температурим зависимость сопротивления. Из формулы удельной проводимости следует, что сопротивление металлов, т. е. величина, обратно пропорциональная у, должна возрастать пропорционально Оценка средней длины свободного пробега электронов в металле. Чтобы получить у, совпадающие с опытными значениями, надо принимать </> значительно больше истинных, другими словами, предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца. Теплоемкость металло в. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. на 1 моль) теплоемкость металла должна быть значительно большей. Наличие электронов проводимости не сказывается на значении теплоемкости, что не объясняется классической электронной теорией. Указанные расхождения теории с опытом можно объяснить тем, что движение в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла-Больцмана, а квантовой статистикой. Недостатки классической электронной теории 1) Учет распределения скоростей электронов (по Максвелу) приводит к худшему согласованию с экспериментальными результатами. 2) Температурная зависимость электропроводности металлов не совпадает с экспериментальной Теория: Эксперимент: 3) Чтобы получить численное совпадение для 4) Вопрос о теплоемкости Согласно МКТ: C=6/2R+3/2R у металлов больше C=6/2R у неметаллов (т.к. нет электрического газа) Малярная теплоемкость всех твердых тел одинакова n=6/2R Вывод: Классическая теория электропроводности многого не учитывает
Тема №18 Закон Ампера Магнитное поле оказывает на рамку с током ориентирующее действие, следовательно, вращающий момент, испытываемый рамкой, есть результат действия силна отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитам поле, равна dF=I[dl,B], где dl — вектор, по модулю равный dl и совпадающий по направлению с током, В — вектор магнитной индукции. Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правши) левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Модуль силы Ампера вычисляется по формуле dF=IBdl sin ά (111.2),где α— угол между векторами dl и В. Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1и I2(направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Ток I1создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора B1 определяется правилом правого винта, его модуль равен μ0μ2I1/4πR
Направление силы dFj, с которой поле В) действует на участок d/ второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (П1.2), с учетом того, что угол а между элементами тока /2 и вектором Bj прямой, Равен dF1=I2B1dl .
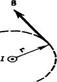
подставляя значение для Въ получим dF1= μ0μ2I1I2dl/4πR Рассуждая аналогично, можно показать, что сила dF2, с которой магнитное поле тока I2 действует на элемент dl первого проводника с током Iь направлена в противоположную сторону и по модулю равна dF2= I1B2dl== μ0μ2I1I2dl/4πR.Сравнение выражений (111.3) и (111.4) показывает, чтоdF1=dF2 т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой dF= μ0μ2I1I2dl/4πR. Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля Если два параллельных проводника с током находятся в вакууме (μ= 1 ), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна dF/dl= Для нахождения числового значения μо воспользуемся определением ампера, согласно которому dF/dl=2-10 7 Н/м при Ii=I2= 1 А и R = 1 м. Подставив это значение в формулу (112.1), получим где генри (Гн) — единица индуктивности (см. § 126). Закон Ампера позволяет определить единицу магнитной индукции B. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111.2)) запишется в виде dF = IBdl, откуда B= Единица магнитной индукции- тесла (Тл): 1 Тл — магнитная индукция однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению магнитного поля, если по этому проводнику проходит ток 1 А: 1 Тл=1 Н/(А*м). Так как μо=4π 10-7 Н/А2, а в случае вакуума (μ= 1), В= μоН, то для данного случая H=B/μо Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4π *10 -7 Тл. 21.. Циркуляция вектора В магнитного поля в вакууме Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной индукции. Циркуляцией вектора В по заданному замкнутому контуру называется интеграл где dl — вектор элементарной длины контура, направленной вдоль обхода контура, Вl=В cos a — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), α— угол между векторами В и dl. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μо на алгебраическую сумму токов, охватываемых этим контуром: ∫Bdl=∫Bldl= μо∑Ik (1) где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Выражение (1) справедливо только для поля в вакууме, поскольку, как будет показано ниже, для поля в веществе необходимо учитывать молекулярные токи. Продемонстрируем справедливость теоремы о циркуляции вектора В на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного к нам. Представим себе замкнутый контур в виде окружности радиуса г (рис). В каждой точке этого контура вектор В одинаков по модулю и направлен по касательной к окружности (она является и линией магнитной индукции). Следовательно, циркуляция вектора В равна ∫B,dl=∫ Bdl=B∫dl=B2πr.
Согласно выражению (1), получим B2πr=μоI (в вакууме), откуда B=μ0I/2πr Таким образом, исходя из теоремы о циркуляции вектора В получили выражение для магнитной индукции поля прямого тока. Сравнивая выражения для циркуляции векторов Е и В, видим, что между ними существует принципиальное различие. Циркуляция вектора Е электростатического поля всегда равна нулю, т. е. электростатическое поле является потенциальным. Циркуляция вектора В магнитного поля не равна нулю. Такое поле называется вихревым. Теорема о циркуляции вектора В имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без применения закона Био — Савара — Лапласа. ABCDA Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС,CD и DA На участках АВ и CD контур перпендикулярен линиям магнитной индукции и Bl=0. На участке вне соленоида В=0. На участке DA циркуляция вектора В равна Вl (контур совпадает с линией магнитной индукции); следовательно, ∫Bldl=Bl= μ0NI. Из этого приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме): B=μ0NI/l Получили, что поле внутри соленоида однородно (краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен. Важное значение для практики имеет также магнитное поле тороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора.Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует. Линии магнитной индукции в данном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса г. Тогда, по теореме о циркуляции B2πr= μ0NI, откуда следует, что магнитная индукция внутри тороида (в вакууме): B= μ0NI/2π где N— число витков тороида. Если контур проходит вне тороида, то токов он не охватывает и В2лг=0. Это означает, что поле вне тороида отсутствует (что показывает и опыт). Билет 32. Индуктивность и емкость в цепи переменного токаю Активное и реактивное сопротивление. Колебательный контур. Гармонические электромагнитные колебания и их характеристики. Дифференциальное уравнение гармонических колебаний и его решение Переменный ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био-Савара пропорциональна току. Поэтому сцепленный с контуром магнитный поток пропорционален току в контуре
Индуктивность контура, в общем случае, зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура – аналог электрической емкости уединенного проводника. Активное сопротивление - величина, характеризующая сопротивление электрической цепи (ее участка) электрическому току, обусловленное необратимыми превращениями электрической энергии в др. формы. выражается отношением активной мощности, поглощаемой на участке цепи, к квадрату действующего значения тока на этом участке. Реактивное сопротивление - величина, характеризующая сопротивление, оказываемое переменному току э лектрическойёмкостью и индуктивностью цепи (её участка). В случае синусоидального тока при последовательном соединении индуктивного и ёмкостного элементов цепи р.с. выражается в виде разности сопротивления индуктивного и сопротивления ёмкостного: Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур – цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатор емкостью С, и резистора сопротивлением R. Уравнение гармонического колебания: Выражение 1
Дифференциальное уравнение свободных гармонических колебаний величины s
Период колебаний физического маятника Период колебаний математического маятника Формула Томпсона Резонанс. Из выражения Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, к примеру, в схемотехнике или геологии. Вопрос №1 Электрический заряд. Дискретность электрического заряда. Элементарный заряд. Закон сохранения электрического заряда. Опыт Милликэна. Закон Кулона. Система единиц. Диэлектрическая постоянная. Линейная, поверхностная и объемная плотность зарядов. Электрический заряд – количественная мера действия степени электризации тел. Элементарный заряд - минимальная порция электрического заряда (e=1.6-19), заряд элементарной частицы (электрон, протон, нейтрон) Электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е. ЗСЭЗ: алгебраическая сумма эл. зарядов любой замкнутой системы не изменяется. Опыт Милликена: (1909) Между пластинами подавалось напряжение и, с помощью пульверизатора, капельки масла, в микроскоп велось наблюдение за установлением равновесия. Нашёл элементарный заряд. Закон Кулона: (1785) Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Точечный заряд - Заряженное тело, размерами которого можно пренебречь по сравнению с расстоянием до других тел.
Также для з.Кулона справедлив принцип суперпозиции: Опытным путём установлено, что взаимодействие двух электрических зарядов не зависит от наличия других зарядов. Диэлектрическая постоянная: Линейная плотность заряда: Поверхностная плотность заряда: Объёмная плотность заряда: Вопрос №2 Электрическое поле, его характеристики. Напряженность поля (точечного заряда и системы зарядов). Вектор электрического смещения. Графическое изображение электрических полей Эл. поле – это пространство, окруж-щее заряж. тела, в кажд. точке этого
|
||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.112.169 (0.02 с.) |

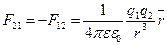
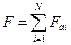 , Fai – сила, с которой действует qa на заряд qi.
, Fai – сила, с которой действует qa на заряд qi.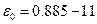 [ ф/м]
[ ф/м] [Кл/м]
[Кл/м] [ кл / м^2 ]
[ кл / м^2 ]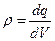 [ кл / м^3 ]
[ кл / м^3 ]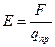

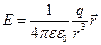
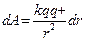
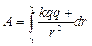

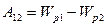
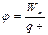

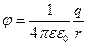
 (алгебраическая сумма потенциалов, создаваемых каждым из зарядов в отдельности)
(алгебраическая сумма потенциалов, создаваемых каждым из зарядов в отдельности)

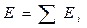
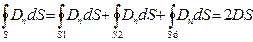
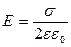

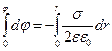
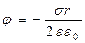

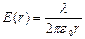
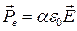 α - поляризуемость молекул (электронная поляризуемость)
α - поляризуемость молекул (электронная поляризуемость)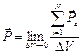 [Кл/м^2]
[Кл/м^2]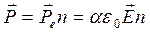
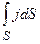 , где dS=ndS (n-единичный вектор нормали к площадке dS, составляющей с вектором j угол
, где dS=ndS (n-единичный вектор нормали к площадке dS, составляющей с вектором j угол 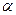 )
)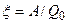
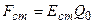
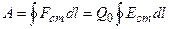
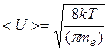 , которая для T=300K равна 1.1*10+5 м/с. Это скорость теплового движения электронов, которое является хаотическим, не может привести к возникновению тока.
, которая для T=300K равна 1.1*10+5 м/с. Это скорость теплового движения электронов, которое является хаотическим, не может привести к возникновению тока.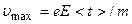
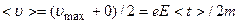
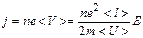
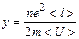
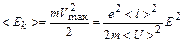
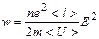
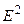 по есть удельная проводимость у; следовательно, выражение
по есть удельная проводимость у; следовательно, выражение 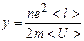 — закон Джоуля — Ленца в дифференциальной форме.
— закон Джоуля — Ленца в дифференциальной форме.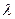 ) к удельной проводимости (у) для всех металлов при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температуре.
) к удельной проводимости (у) для всех металлов при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температуре.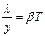 , где
, где 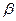 -постоянная, зависящая от рода металла.
-постоянная, зависящая от рода металла.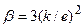 , где k - постоянная Больцмана. Это значение хорошо согласуется с опытными данными. Однако, как оказалось впоследствии, это согласие теоретического значения с опытным случайно; Лоренц, применив к электронному газу статистику Максвелла — Больцмана, учтя тем самым распределение электронов скоростям, получил,
, где k - постоянная Больцмана. Это значение хорошо согласуется с опытными данными. Однако, как оказалось впоследствии, это согласие теоретического значения с опытным случайно; Лоренц, применив к электронному газу статистику Максвелла — Больцмана, учтя тем самым распределение электронов скоростям, получил, 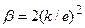 что привело к резкому расхождению теории c опытом. Таким образом, классическая теория электропроводности металлов объяснила законы Ома и Джоуля — Ленца, а также дала качественное объяснение закона Видемана — Франца. Однако она помимо рассмотренных противоречий в законе Видемана- Франца столкнулась еще с рядом трудностей при объяснении различных опытных данных.
что привело к резкому расхождению теории c опытом. Таким образом, классическая теория электропроводности металлов объяснила законы Ома и Джоуля — Ленца, а также дала качественное объяснение закона Видемана — Франца. Однако она помимо рассмотренных противоречий в законе Видемана- Франца столкнулась еще с рядом трудностей при объяснении различных опытных данных.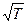 Этот вывод электронной теории противоречит опытным данным ,
Этот вывод электронной теории противоречит опытным данным ,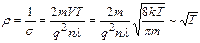
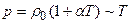
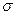 в теории с экспериментом, надо считать, что
в теории с экспериментом, надо считать, что 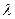 составляет примерно 100 межатомных расстояний.
составляет примерно 100 межатомных расстояний.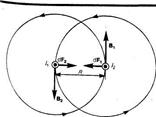
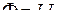 , где коэф. Пропорциональности L называется индуктивностью контура
, где коэф. Пропорциональности L называется индуктивностью контура
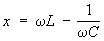 , где w - угловая частота тока, L и С - индуктивность и ёмкость цепи
, где w - угловая частота тока, L и С - индуктивность и ёмкость цепи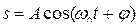 , где
, где 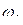 - циклическая частота (величина обратная периоду)
- циклическая частота (величина обратная периоду)
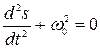 Решением этого уравнения является выражение 1
Решением этого уравнения является выражение 1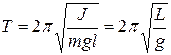
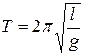

 следует, что если затухание в системе отсутствует
следует, что если затухание в системе отсутствует  ,то только в этом случае колебания и вынуждающая сила(приложенное переменное напряжение)имеют одинаковые фазы; во всех других случаях
,то только в этом случае колебания и вынуждающая сила(приложенное переменное напряжение)имеют одинаковые фазы; во всех других случаях  .При изменении
.При изменении 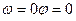 , а при
, а при 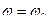 независимо от значения коэффециента затухания
независимо от значения коэффециента затухания 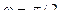 , т.е. сила(напряжение) опережает по фазе колебания на
, т.е. сила(напряжение) опережает по фазе колебания на 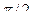 .При дальнейшем увеличении
.При дальнейшем увеличении 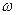 сдвиг фаз возрастает и при
сдвиг фаз возрастает и при 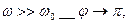 т.е. фаза колебаний почти противоположна фазе внешней силы(переменного напряжения).
т.е. фаза колебаний почти противоположна фазе внешней силы(переменного напряжения).


