
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжённость поля системы зарядов:Содержание книги
Поиск на нашем сайте
Вектор электрического смещения: D=Eεε
Графическое изображение электрических полей: Линии напряжённости проводят так, что касательная к ним в каждой точке совпадает с направлением вектора Е. Густота линий выбирается так, что кол-во линий, пронизывающих единицу пов-ти, перпендикулярной к линиям площадки, было равно числовому значению Е. Вопрос №3 Работа перемещения электрического заряда в электрическом поле. Теорема о циркуляции вектора напряженности электрического поля. Потенциал электрического поля. Разность потенциалов. Эквипотенциальные поверхности. Потенциал поля точечного заряда и системы зарядов.
Кулоновская сила консервативна, а электростатическое поле - потенциально. Работа сил консервативного поля – убыль потенциальной энергии.
Потенциал: скал. физ. велич., равная потенц. эн., которой обладает ед. пол. заряд, помещ. в данную точку. (Wп/qпр) Потенциал поля точечного заряда: Потенциал поля системы зарядов: Wn=φq A=W1-W2 =q(φ1 – φ2) A=qφ (если заряд из точки с потенциалом φ удаляется на бесконечность)=> Потенциал: численно равен работе, которую совершают силы поля над единичным полож. зарядом при удалении его из данной точки на бесконечность.
Теорема о циркуляции вектора напряжённости (признак потенциальности поля): циркуляция вектора Е равна нулю. Эквипотенциальные поверхности: воображаемые пов-ти, все точки которых имеют одинаковый потенциал. Уравнение такой пл-ти: φ(x,y,z)=Const Вектор Е в каждой точке направлен по нормали к эквипот. пов-ти. Линии напряжённости в каждой точке ортогональны к эквипот. пов-тям. Эквипот. пов-ть можно провести через любую точку поля => по густоте эквипот. пов-тей можно судить о величине напряжённости поля. Билет №4 Связь напряженности электрического поля с потенциалом. Применение этой связи для расчета эл. полей.
dA = qEdl = qEdlCos@ = qEldl; dA = -dWn = -qdφ =>
Зная Е можно найти разность потенциалов между двумя произвольными точками поля:
Билет №5 Принцип суперпозиции Эл. Полей. Расчет поля (напряженности и потенциала) заряженной нити, кольца Принцип суперпозиции эл. полей: Напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создавал бы каждый из зарядов в отдельности.
Напряжённость заряженной нити:
Выберем беск. малый эл-нт dl
Частные случаи: 1) r0 -> ∞ @1 = π/2 @2 = π/2 2)Против среза нити @1 = π/2 @2 = 0 3)Против середины нити @1 = -@2
|
||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.054 с.) |

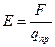
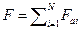
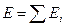
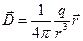
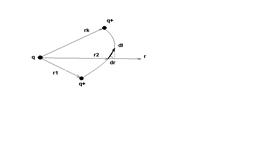
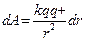
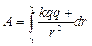

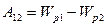
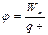

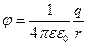
 (алгебраическая сумма потенциалов, создаваемых каждым из зарядов в отдельности)
(алгебраическая сумма потенциалов, создаваемых каждым из зарядов в отдельности)

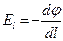
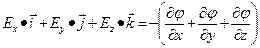
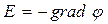
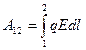 и
и 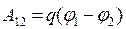 =>
=> 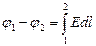
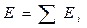

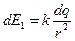
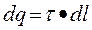

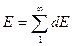
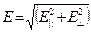

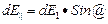
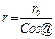
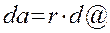 | =>
| => 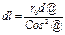
 |
|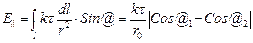
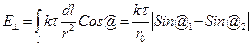
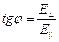
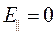
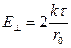


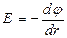 =>
=> 



