
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В каких единицах измерения измеряются относительные величины?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
__________________________________________________________________ В чем суть базисного метода расчета относительных величин? __________________________________________________________________ В чем суть расчета относительной статистической величины с переменной базой сравнения? __________________________________________________________________ __________________________________________________________________ Контрольный тест по теме Абсолютные и относительные величины в статистике 1. Абсолютные показатели могут выражаться: а) в натуральных единицах измерения б) в процентах; 2. Показатели, выражающие размеры, объем, уровни социально-экономических явлений и процессов, являются величинами: а) абсолютными; б) относительными. 3. Абсолютные величины могут выражаться в единицах измерения: а) натуральных и условно-натуральных; б) трудовых и денежных; в) отвлеченных. 4. Абсолютные величины выражаются в единицах измерения: а) килограммах, штуках, метрах, тоннах, километрах и т.д.; б) коэффициентах, процентах, промилле, продецимилле. 5. Виды абсолютных величин: а) индивидуальные, общие; б) выполнение плана, планового задания, динамики, структуры, координации, сравнения, интенсивности. 6. Объемные абсолютные величины получаются в результате: а) сложения индивидуальных абсолютных величин; б) подсчета числа единиц, входящих в каждую группу или совокупность в целом. 7. Относительные величины выполнения плана исчисляются как: а) отношение планового задания на предстоящий период к фактически достигнутому уровню, являющемуся базисным для плана; б) отношение фактически достигнутого уровня к плановому заданию за тот же период времени. 8. Относительные величины динамики получаются в результате сопоставления показателей каждого последующего периода: а) с предыдущим; б) с первоначальным; в) со средним. 9. Относительные величины структуры: а) характеризуют состав явления и показывают, какой удельный вес в общем итоге составляет каждая его часть; б) показывают соотношение отдельных составных частей целого явления. 10. Относительные величины интенсивности представляют собой: а) отношение двух разноименных показателей, находящихся в определенной взаимосвязи; б) отношение двух одноименных показателей, относящихся к разным объектам или территориям за один и тот же период или момент времени. 11.Относительные величины структуры: а) характеризуют состав явления и показывают, какой удельный вес в общем итоге составляют каждая его часть; б) показывают соотношение отдельных составных частей целого явления. 12. Относительными статистическими показателями не могут быть: а) показатели структуры; б) натуральные показатели; в) показатели динамики; г) показатели сравнения. 13. Относительные статистические показатели выражаются: а) в стоимостных единицах измерения; б) в промилле; в) в чел./днях. 14. Показатели выражающие размеры, объем, уровни социально-экономических явлений и процессов, являются величинами: а) абсолютными; б) относительными. Тема 6. Средние показатели и показатели вариации Цель: Закрепить знания по теме «Средние показатели и показатели вариации» Краткая теория Понятие вариационного ряда.Первым шагом систематизации материалов статистического наблюдения является подсчет числа единиц, обладающих тем или иным признаком. Расположив единицы в порядке возрастания или убывания их количественного признака и подсчитав число единиц с конкретным значением признака, получаем вариационный ряд. Вариационный ряд характеризует распределение единиц определенной статистической совокупности по какому–либо количественному признаку. Вариационный ряд представляет собой две колонки, в левой колонке приводятся значения варьирующего признака, именуемые вариантами и обозначаемые (x), а в правой – абсолютные числа, показывающие, сколько раз встречается каждый вариант. Показатели этой колонки называются частотами и обозначаются (f). Схематично вариационный ряд можно представить в виде табл.2: Таблица 2 Вид вариационного ряда
В правой колонке могут использоваться и относительные показатели, характеризующие долю частоты отдельных вариантов в общей сумме частот. Эти относительные показатели именуют частостями и условно обозначают через Варьирующие признаки могут носить разный характер. Варианты одних признаков выражаются в целых числах, например, число комнат в квартире, число изданных книг и т.д. Эти признаки именуют прерывными, или дискретными. Варианты других признаков могут принимать любые значения в определенных пределах, как, например, выполнение плановых заданий, заработная плата и др. Эти признаки называют непрерывными. Интервальный вариационный ряд. Для непрерывных признаков вариационные ряды строятся интервальные, т.е. значения признака в них выражаются в виде интервалов «от и до». При этом минимальное значение признака в таком интервале именуют нижней границей интервала, а максимальное – верхней границей интервала. + Интервальные вариационные ряды строят как для прерывных признаков (дискретных), так и для варьирующих в большом диапазоне. Интервальные ряды могут быть с равными и неравными интервалами. В экономической практике в большинстве своем применяются неравные интервалы, прогрессивно возрастающие или убывающие. Такая необходимость возникает особенно в тех случаях, когда колеблемость признака осуществляется неравномерно и в больших пределах. Плотность распределения. Однако частоты отдельных неравных интервалов в названных рядах непосредственно не сопоставимы. В подобных случаях для обеспечения необходимой сравнимости исчисляют плотность распределения, т.е. определяют, сколько единиц в каждой группе приходится на единицу величины интервала. При построении графика распределения вариационного ряда с неравными интервалами высоту прямоугольников определяют пропорционально не частотам, а показателям плотности распределения значений изучаемого признака в соответствующих интервалах. Составление вариационного ряда и его графическое изображение является первым шагом обработки исходных данных и первой ступенью анализа изучаемой совокупности. Следующим шагом в анализе вариационных рядов является определение основных обобщающих показателей, именуемых характеристиками ряда. Эти характеристики должны дать представление о среднем значении признака у единиц совокупности. Средняя величина. Средняя величина представляет собой обобщенную характеристику изучаемого признака в исследуемой совокупности, отражающая ее типический уровень в расчете на единицу совокупности в конкретных условиях места и времени. Средняя величина всегда именованная, имеет ту же размерность, что и признак у отдельных единиц совокупности. Перед вычислением средних величин необходимо произвести группировку единиц исследуемой совокупности, выделив качественно однородные группы. Средняя, рассчитанная по совокупности в целом называется общей средней, а для каждой группы – групповыми средними. Существуют две разновидности средних величин: степенные (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая); структурные (мода, медиана, квартили, децили). Выбор средней для расчета зависит от цели. Мода. Модой (Мо) называется наиболее часто встречающееся значение признака у единиц совокупности. Модой называется то значение признака, которое соответствует максимальной точке теоретической кривой распределения. Мода широко используется в коммерческой практике при изучении покупательского спроса (при определении размеров одежды и обуви, которые пользуются широким спросом), регистрации цен. Мод в совокупности может быть несколько. Медиана. Медианой ( Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Колеблемость отдельных значений характеризуют показатели вариации. Чем больше вариация, тем дальше в среднем отдельные значения лежат друг от друга. Различают вариацию признака в абсолютных и относительных величинах. + К абсолютным показателям относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия. Все абсолютные показатели имеют ту же размерность, что и изучаемые величины. К относительным показателям относятся коэффициенты осцилляции, линейного отклонения и вариации. Практические задания 1. Средняя величина – это ___________________________________________ __________________________________________________________________
|
||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 1071; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.13.111 (0.013 с.) |

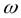 , т.е.
, т.е. 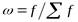 . Сумма всех частостей равна единице. Частости могут быть выражены и в процентах, и тогда их сумма будет равна 100%.
. Сумма всех частостей равна единице. Частости могут быть выражены и в процентах, и тогда их сумма будет равна 100%.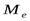 ) называется значение признака у средней единицы ранжированного ряда. Ранжированный ряд – это ряд, у которого значения признака записаны в порядке возрастания или убывания. Или медиана это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значение варьирующего признака меньшие, чем средний вариант, а другая – большие.
) называется значение признака у средней единицы ранжированного ряда. Ранжированный ряд – это ряд, у которого значения признака записаны в порядке возрастания или убывания. Или медиана это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значение варьирующего признака меньшие, чем средний вариант, а другая – большие.


