Решение систем нелинейных уравнений

Для решения системы нелинейных уравнений нужно выполнить операции:

1. Выделить рабочие ячейки для неизвестных переменных и ввести в них любые числовые значения переменных из предполагаемой области их определения.

2. В рабочих ячейках записать формулы каждой из функций, составляющих систему в терминах табличного процессора.

3. Включить инструмент Поиск решения. В качестве целевой ячейки указать ячейку, в которой записана формула одной из функций системы. Установить переключатель Значению и в соответствующем поле ввести числовое значение ноль. В поле изменяемых ячеек указать диапазон ячеек, которые определены для вычисления неизвестных переменных. На вычисляемые значения в других ячейках, содержащих формулы оставшихся функций, наложить ограничения на равенство нулю. В окне поиска решения следует выбрать «Поиск решения нелинейных задач». Выполнить решение.

 

Пример 7.3. Решить систему нелинейных уравнений:

у = 2/х

у² = 2х

на отрезке х ϵ [-2, 2].

Решение. В ячейки А3 и В3 рабочего листа введем любые числа из диапазона, например, 1 и 1. В ячейки В5 и В6 – формулы: =2/A3-B3 и =B3^2-2*A3 соответственно (рис. 50). Вызовем Поиск решения. В качестве целевой функции укажем ячейку В5 и установим переключатель Значение равным 0. В качестве изменяемых ячеек укажем ячейки А3 и В3, а в качестве ограничения – равенство 0 второго уравнения, находящегося в ячейке В6. В результате поиска будет найдено решение: х = 1,259921; у = 1,587401.

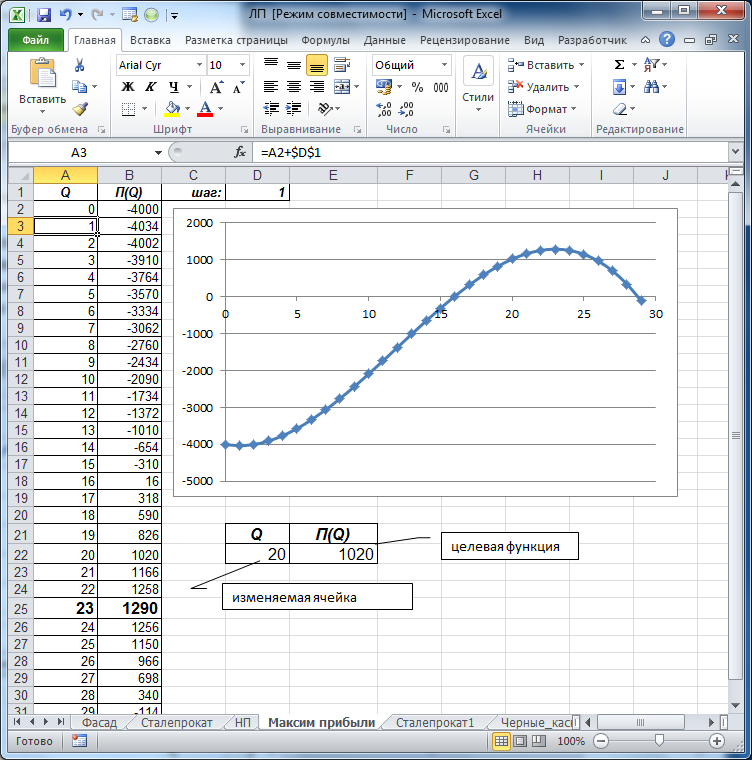
Рис. 50. Решение системы нелинейных уравнений

Максимизация прибыли

Пусть Q – количество реализованного товара, R(Q) – функция дохода; C(Q) – функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры и т.п. Прибыль от реализации произведенного товара дается формулой

П(Q) = R (Q) – C (Q).

Пример7.4. Найти максимум прибыли, если доход и издержки определяются следующими формулами:

R (Q) = 100 Q – Q ²

C (Q) = Q ³ – 37 Q ² + 169 Q + 4000.

Решение. Согласно приведенной выше формуле, прибыль П(Q) = -Q³ + 36Q² – 69Q – 4000.

Поскольку количество – величина положительная, построим график функции на отрезке [ 0; 30 ] с шагом 1, для чего построим таблицу значений для Q и П(Q) (В2 = –A2^3+36*A2^2–69*A2–4000). Проанализировав внешний вид графика, можно утверждать, что максимум функции находится в окрестности точки со значением х = 20. Введем это значение в изменяемую ячейку D 22, а в ячейку Е22 скопируем формулу вычисления прибыли: = –D22^3+36*D22^2–69*D22–4000 (рис. 51).

Рис. 51. Решение системы нелинейных уравнений

Ячейка Е22 содержит целевую функцию, которую необходимо максимизировать. В надстройке Поиск решения укажем ее в качестве целевой ячейки, в качестве изменяемой ячейки укажем ячейку D 22, ограничения в этой задаче отсутствуют. В результате поиска решения получим значение Q = 23, при этом П(Q)=1290, это и есть максимальная прибыль.

Можно проверить решение задачи аналитически: приравнивая производную функции прибыли к нулю, получаем уравнение

C ’(Q) = 3 Q ² – 72 Q + 169 ®  - Q ² + 24 Q – 23 = 0.

Корни этого уравнения Q₁ = 1, Q₂ = 23, причем при переходе через точку Q = 23 производная меняет знак с плюса на минус. Следовательно, Q = 23 – точка локального максимума, при этом прибыль равна: П_mах = 1290.

Задания для самостоятельного выполнения

Задание 7.1. Цена за единицу товара составляет 250 рублей. Издержки производства определяет функция C(x) = 120x + x², где х – число единиц произведенного товара. Найти максимальное значение прибыли.

Задание 7.2. Издержки производства некоторой продукции определяются функцией C(x)= 5x² + 80x, где х – число единиц произведенной за месяц продукции. Эта продукция продается по цене 280 рублей за изделие. Сколько изделий нужно произвести и продать, чтобы прибыль была максимальной?

Задание 7.3. Известно, что цена продажи акций A, B и C до начала предстоящего месяца составляет 34,30; 74,87; 107,00 руб. В распоряжении инвестора имеется капитал 73 тыс. руб. Инвестора интересует вопрос, акции какого эмитента и в каком количестве следует приобрести по сегодняшнему курсу продажи, чтобы с минимальным риском получить в предстоящем месяце доход от портфеля не менее 55,41% на вложенный капитал. Ретроспектива динамики курсов:

Таблица 32.

Месяц	1	2	3	4	5	6	7	8	9	10
Курс А	130	85	53,5	35,42	31,44	34,74	33,4	40,96	35,01	35,89
Див. от А	1,2	2,86	48,2	23,94	4,96	0,04	11,3	20,82	1,33	0,26
Курс В	66	64,19	64,19	61,37	51,88	65,85	88,9	77,57	56,68	65,41
Див от В	0,05	4,71	7,53	56,95	20,96	34,5	0,03	73,12	12,7	14,59
Курс С	48	60,95	60,95	58,23	50,38	51,87	72,1	105,95	73,14	89,94
Див. от С	19,42	16,71	7,24	47,11	2,24	30,32	50,8	114,84	25,2	25,59

 

Задание 7.4. Решить систему нелинейных уравнений:

х + у – 8 = 0

х² + у² = 82

на отрезке х ϵ [-2, 10].

Задание 7.5. Зависимость спроса y на некоторый товар от цены x выражается функцией y =2/x + 2, а зависимость предложения от цены – функцией y = x² + 1. Требуется найти точку равновесия (спрос равен предложению) в диапазоне х ϵ [ 0,2; 3 ].