Решение систем линейных уравнений методом Гаусса

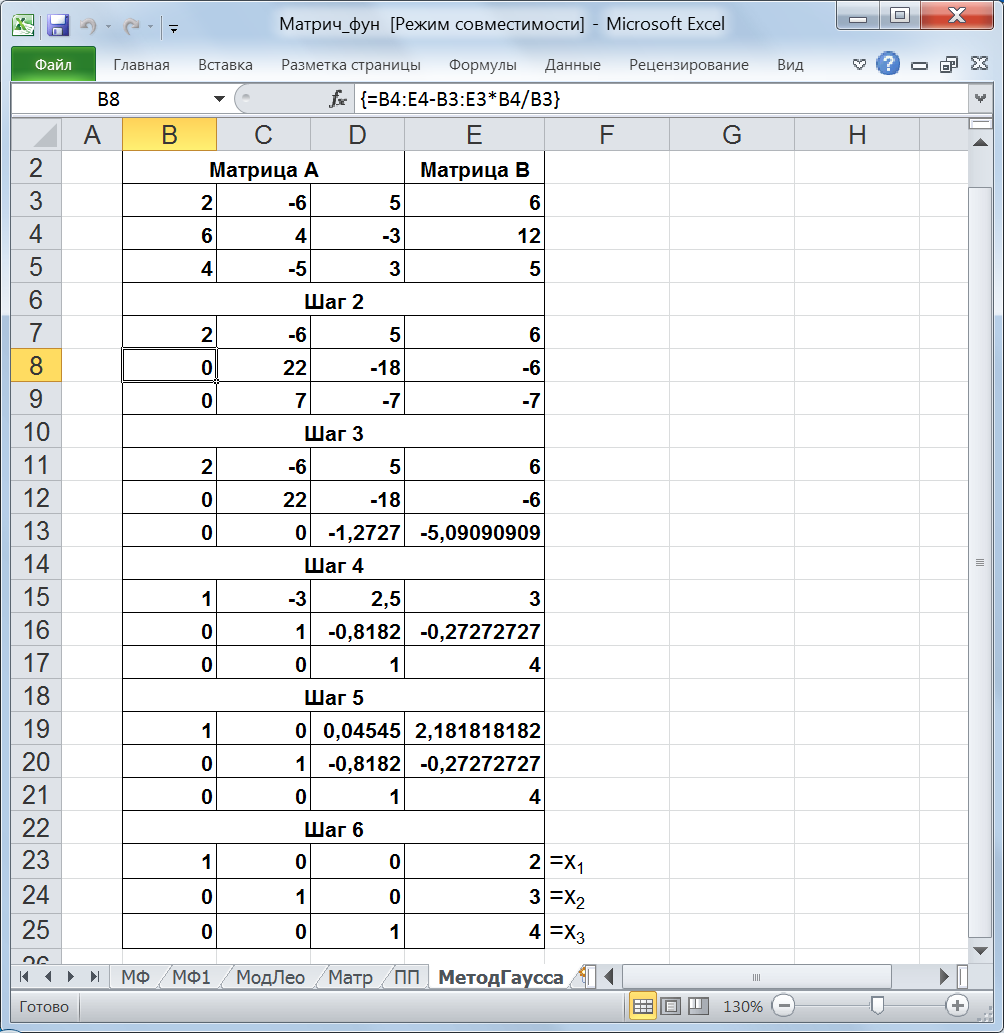
Метод Гаусса состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы ее матрица, составленная из коэффициентов, оказалась трапециевидной:

a ₁₁ х₁ + а₁₂х₂ + … + а_1nx_n = b₁

a ₂₂ х₂ + … + а_2nx_n = b₂

…………

а _{n n} x_n = b _n

В такой системе последнее уравнение содержит только одну переменную и ее значение можно найти однозначно. Затем значение этой переменной подставляют в предыдущее уравнение, из которого находят предыдущую переменную, и т.д.

После того, как матрица системы примет трапециевидную форму, находится решение системы. Методом Гаусса также можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений.

Пример 5.6. Решите систему линейных уравнений методом Гаусса:

2х₁ – 6х₂ + 5х₃ = 6

6х₁ + 4х₂ – 3х₃ = 12

4х₁ – 5х₂ + 3х₃ = 5

Решение. Введем матрицу А в диапазон B3:D5, матрицу В – в диапазон Е3:Е5 (рис. 30). (Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение).

Приведем все коэффициенты при x₁ к 0, кроме первого уравнения. Скопируем значения первой строки матриц А и В в диапазон ячеек В7:Е7. Выделим диапазон ячеек В8:Е8 и введем формулу:

= B4:E4 – B3:E3 * В4/B3.

Нажмем сочетание клавиш Ctrl + Shift + Enter.

Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения (рис. 30, Шаг 2).

Выделим диапазон ячеек В9:Е9 и введем формулу:

= B5:E5 – B3:E3 * В5/B3.

Нажмем сочетание клавиш Ctrl + Shift + Enter.

Мы отняли от третьей строки первую, умноженную на отношение первых элементов третьего и первого уравнения (рис. 30, Шаг 2).

Теперь приведем коэффициенты перед x₂ в третьем уравнении к 0. Скопируем полученные значения из диапазона В7:Е8 в диапазон ячеек В11:Е12. Выделим диапазон ячеек В13:Е13 и введем формулу:

  = B9:E9 – B8:E8 * С9/С8.

Нажмем сочетание клавиш Ctrl + Shift + Enter (рис. 30, Шаг 3).

Рис. 30. Решение системы уравнений методом Гаусса

Трапециевидная матрица получена. Далее находим непосредственно решение системы. Для этого проделаем шаги 4 – 6.

Все элементы первой строки необходимо поделить на коэффициент при х₁, второй строки на коэффициент при х₂, третьей строки на коэффициент при х₃.

Для этого выделим диапазон В15:Е15, введем формулу =B11:E11/В11, нажмем сочетание клавиш Ctrl + Shift + Enter (рис. 30, Шаг 4).

Далее выделим диапазон В16:Е16, введем формулу =B12:E12/С12, нажмем сочетание клавиш Ctrl + Shift + Enter (рис. 30, Шаг 4).

И, наконец, выделим диапазон В17:Е17, введем формулу =B13:E13/D13, нажмем сочетание клавиш Ctrl + Shift + Enter (рис. 30, Шаг 4). В первом столбце В все готово, т.е. мы имеем в столбце единственное равное 1 значение в ячейке В15.

На пятом шаге необходимо получить во втором столбце С ситуацию, когда там останется единственное равное 1 значение в ячейке С16, т.е. необходимо обнулить ячейку С15.

Скопируем диапазон ячеек В16:Е17 и вставим в диапазон ячеек В20:Е21. Выделим диапазон ячеек В19:Е19 и введем формулу:

=B15:E15 – B16:E16*C15.

Нажмем сочетание клавиш Ctrl + Shift +Enter (рис. 30, Шаг 5).

На шестом шаге скопируем диапазон ячеек В21:Е21 и вставим в диапазон ячеек В25:Е25. Выделим диапазон ячеек В24:Е24 и введем формулу:

=B20:E20 – B21:E21*D20.

Нажмем сочетание клавиш Ctrl + Shift +Enter (рис. 30, Шаг 6).

Выделим диапазон ячеек В23:Е23 и введем формулу:

= =B19:E19 – B21:E21*D19.

Нажмем сочетание клавиш Ctrl + Shift +Enter (рис. 30, Шаг 6).

В результате в диапазоне ячеек Е23:Е25 отобразиться решение системы линейных уравнений, то есть следующие результаты: x₁=2, x₂=3, x₃=4.

 

Пример 5.7.

В таблице приведены данные о дневной производительности пяти предприятий холдинга, выпускающих четыре вида продукции с использованием трех видов сырья, а также продолжительность работы каждого предприятия в году и цена каждого вида сырья.

Таблица 9.

Вид изделия №	Производительность предприятия (изд. / день)					Затраты видов сырья (ед. веса / изд.)
	1	2	3	4	5	1	2		3
1	4	5	3	6	7	1	2		3
2	0	2	4	3	0	3	5		6
3	8	15	0	4	6	4	4		5
4	3	10	7	5	4	5	8		6
	Количество рабочих дней в году					Цены видов сырья (ден. ед. / ед. веса)
	1	2	3	4	5	1	2	3
	200	150	170	120	140	40	50	60

 

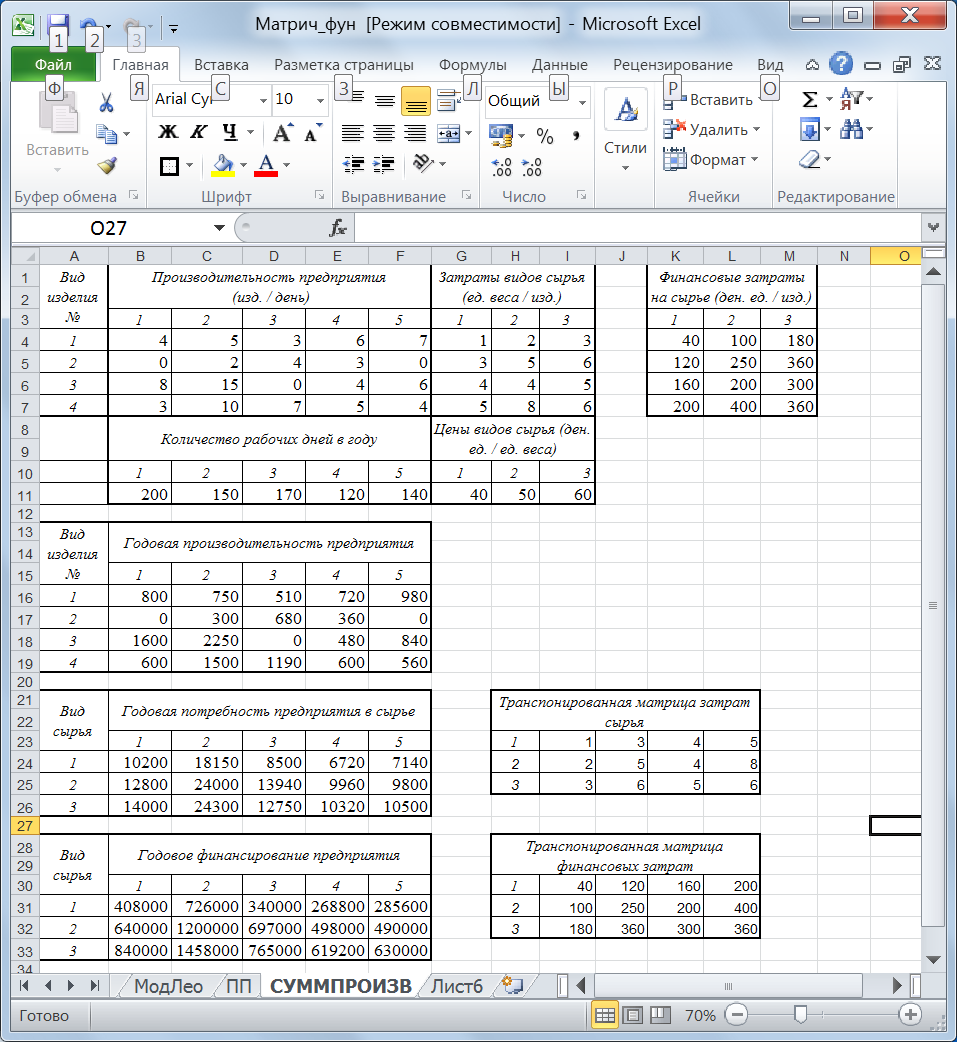
Требуется определить: годовую производительность каждого предприятия по каждому виду изделий; годовую потребность каждого предприятия в каждом виде сырья; годовую сумму финансирования каждого предприятия холдинга для закупки сырья, необходимого для выпуска продукции.

Решение. Перенесем исходные данные на лист Excel. Компьютерная модель задачи имеет вид (рис. 31).

Для расчета годовой производительности каждого предприятия необходимо найти произведение количества произведенных изделий в день каждым предприятием на количество рабочих дней в году каждого предприятия. Для этого выделим весь диапазон В16: F 19 и введем формулу: =B4:F7*B11:F11, закончив ее ввод сочетанием клавиш Shift+Ctrl+Enter.

Рис. 31. Компьютерная модель примера 5.5.

Аналогично рассчитаем матрицу финансовых затрат на каждый вид сырья для каждого изделия (диапазон (K 4:М7): {=G4:I7*G11:I11}).

Для расчета годовой потребности каждого предприятия в каждом виде сырья необходимо найти сумму произведений годового выпуска каждого изделия на затраты каждого вида сырья на единицу изделия. Для этого транспонируем матрицу затрат видов сырья. Для первого изделия в диапазоне В24:В26 найдем произведение полученной транспонированной матрицы (диапазон I 23: L 25) на вектор годовой производительности первого предприятия (диапазон В16:В19). Формулу скопируем вправо для расчета годовой потребности в сырье других предприятий (в диалоговом окне функции МУМНОЖ не забудьте закрепить общий для всех диапазон I 23: L 25!).

Аналогично рассчитаем годовое финансирование для каждого предприятия на закупку сырья предварительно транспонировав в диапазоне I 30: L 32 матрицу финансовых затрат на сырье (диапазон К4:М7). Результаты всех расчетов приведены на рисунке 31.

Пример 5.8. Известно, что рациональное функционирование многоотраслевого хозяйства предполагает соблюдение баланса между отраслями. Каждая отрасль многоотраслевого хозяйства является, с одной стороны, производителем определенной продукции, а с другой – потребителем продукции, выпускаемой другими отраслями. Макроэкономика функционирования многоотраслевого хозяйства требует, чтобы соблюдался баланс по производству и потреблению между отдельными отраслями.

Балансовый принцип связи различных отраслей состоит в том, что валовой выпуск i-й отрасли должен быть равен сумме объемов потребления. В простейшей форме балансовые соотношения имеют вид:

x_i = x_{i 1} + x_{i 2} + … + x_{i n} + y_i, i = 1, 2, …, n,

где x_i — общий объем выпускаемой продукции i -й отрасли;

x_ij — объем продукции i -й отрасли, потребляемый j -й отраслью при производстве объема продукции x_j;

y_i — объем продукции i-й отрасли конечного потребления (для реализации в непроизводственной сфере). Сюда относятся личное потребление граждан, удовлетворение общественных потребностей, содержание государственных институтов и т.д.

Для производства продукции j -й отрасли объемом x_i нужно использовать продукцию i -й отрасли объемом a_ijx_i, где а_ij — постоянное число, характеризующее прямые затраты.

Это допущение позволяет представить модель многоотраслевой экономики (модель Леонтьева) в виде системы линейных уравнений, которая в матричной форме имеет вид Х = AХ + Y, (А= П / X^T, П{Х_ij} –матрица потребления, т.е. a_ij = Х_ij / Х _i),

где X — вектор валового выпуска;

Y — вектор объема продукции конечного потребления;

A — матрица прямых затрат.

Приведенная система уравнений может быть представлена в виде

(E – A) X = Y, где E — единичная матрица.

Если существует обратная матрица (E – A)^–1 (матрица полных затрат), то существует единственное решение системы X = (E – A)^–1 Y.

В таблице приведены данные об исполнении баланса за отчетный период (у.е.):

Таблица 10.

отрасль	потребление		конечный продукт	валовой выпуск
	I	II
I	7	21	72	100
II	12	15	123	150

Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление I-ой отрасли увеличится вдвое, а II-ой сохранится на прежнем уровне.

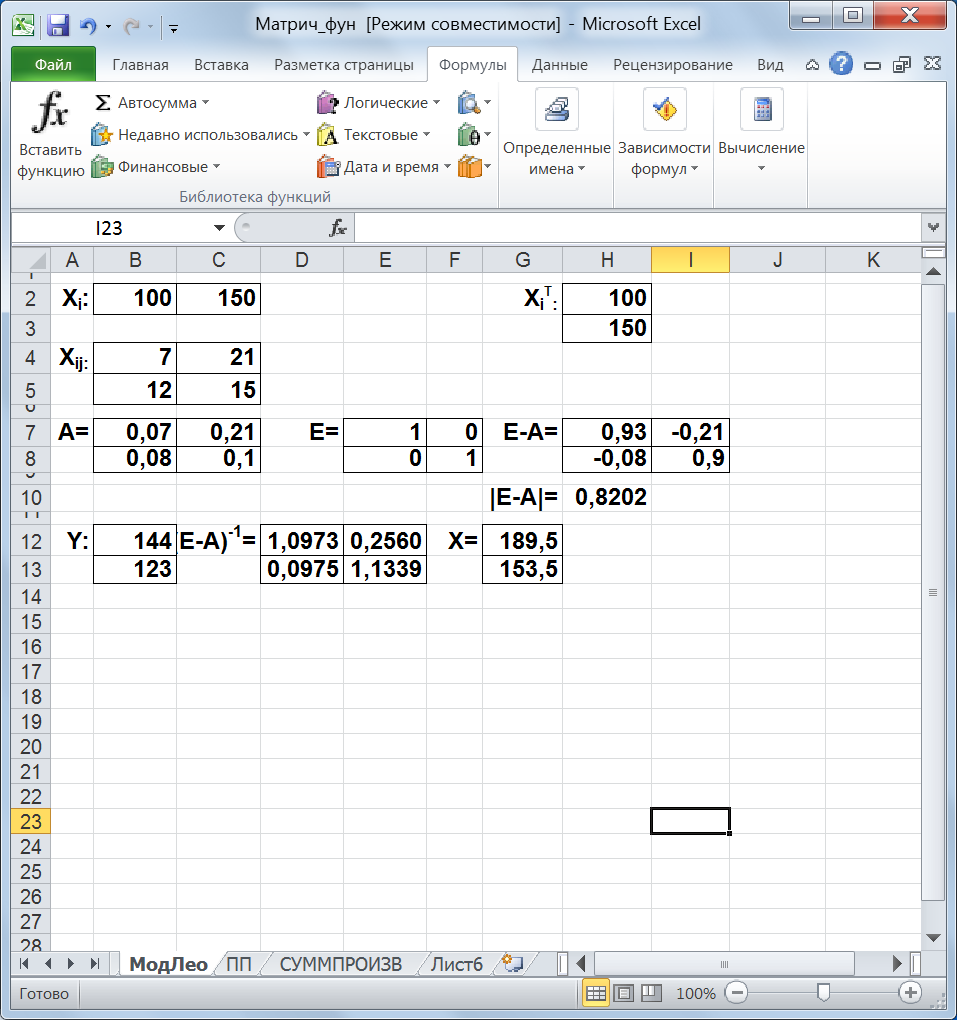
Решение. На лист Excel введем данные для вектор X _i, матриц X _{i j}, Е, новый вектор Y, а также свободные диапазоны для матриц X _i ^T, А, (E-A), (E-A) ^-1 и результирующего вектора Х (рис. 33). Рассчитаем матрицы X _i ^T, А и Е-А по формулам, представленным на рисунке 32.

Определитель матрицы | Е-А | = 0,8202 ≠ 0, так что обратная матрица и решение указанной системы уравнений существуют. Найдем его с использованием встроенных функций МОБР и МУМНОЖ (рис. 33).

Таким образом, согласно рис. 33, в I-ой отрасли валовой выпуск надо увеличить до 189,5 у.е., а во II-ой — до 153,5 у.е.

 

Рис. 32. Формулы расчетов матриц А и Е-А

Рис. 33. Решение балансовых экономических моделей

Задания для самостоятельного выполнения

Задание 5.1

Предприятие ежесуточно выпускает четыре вида изделий, производственно-экономические показатели которых приведены в таблице:

Таблица 11.

Вид изделия	Количество выпускаемых изделий, шт.	Расход сырья, кг/изд.	Норма времени изготовления, ч/изд.	Стоимость изделия, ден. ед/изд.
	N	P	T	Ц
1	20	5	10	30
2	50	2	5	15
3	30	7	15	45
4	40	4	8	40

 

Требуется определить следующие ежесуточные показатели: расход сырья S, затраты рабочего времени Т и стоимость Р выпускаемой продукции предприятия.

 

Задание 5.2. Найти произведение матриц:

1)

2 -1 1 1

1 3 2 6

1 1 2 -1

9 6 -3 2

                                                            2)

 

3)

3 5 -1 1 -2 0

2 4 -3 0  5 1

2 3 -4 -1 -1 3  1 -2 5

1 2 3 3 -1 1 1 2 2

                                                         4)

 

 

1 -1 3

4 3  2

1 2 -3

3 1 -1 4 -1 3 2 6 0

5)                                                                6)

Задание 5.3

Используя операции с матрицами, решите систему уравнений:

х₁ + 2х₂ + 8х₃ + 22 = 0

х₁ – х₂ + х₃ + 2,5 = 0

10х₁ – 3х₂ – 19 = 0

Задание 5.4

Решите систему уравнений методом Крамера:

5х₁ + 3х₂ – х₃ = 8

2х₁ – 4х₂ + 3х₃ = 3

7х₁ + 4х₂ – 2х₃ = 9

 

Задание 5.5

Решите систему уравнений методом наименьших квадратов:

8х₁ + 5х₂ = 10

5х₁ + 2х₂ = 4

7х₁ + 4х₂ = 8

 

Задание 5.6.

Ресторан специализируется на выпуске трех видов фирменных блюд: В1, В2, ВЗ, при этом используются ингредиенты трех типов S1, S2, S3. Нормы расхода каждого из них на одно блюдо и объем расхода ингредиентов на 1 день заданы таблице 12. Найти расход каждого ингредиента, если выпускается по 250 единиц каждого блюда. Хватит ли имеющихся запасов?

Таблица 12.

Ингредиент	Нормы расхода ингредиентов на 1 блюдо  (у. е.)			Запас ингредиентов на 1 день (у. е.)
	В1	В2	В3
S1	4	6	5	3650
S2	2	3	1	1550
S3	1	4	3	2100

 

Задание 5.7.

В таблице приведены данные по балансу за некоторый период времени между пятью отраслями.

Таблица 13.

№	Отрасль	Потребление					Конечный продукт	Валовой выпуск (ден.ед)
		1	2	3	4	5
1	Станкостроение	15	12	24	23	16	10	100
2	Энергетика	10	3	35	15	7	30	100
3	Машиностроение	10	5	10	10	10	5	50
4	Автомобильная промышленность	10	5	10	5	5	15	50
5	Добыча и переработка углеводородов	7	15	15	3	3	50	100

 

Требуется найти векторы конечного потребления и валового выпуска, а также матрицу коэффициентов прямых затрат и определить ее продуктивность.

В приведенной таблице в первых пяти столбцах (группа “Потребление”) содержатся значения x_ij, в последнем столбце содержатся элементы вектора валового выпуска x, в предпоследнем столбце – элементы вектора объема конечного потребления y.

Задание 5.8. В таблице приведены данные по балансу за некоторый период времени между тремя отраслями.

Таблица 14.

№	Отрасль	Потребление			Конечный продукт	Валовой выпуск (ден.ед)
		1	2	3
1	Добыча и переработка углеводородов	5	35	20	40	100
2	Энергетика	10	10	20	60	100
3	Машиностроение	20	1	10	10	50

 

Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить, соответственно, до 60, 70 и 30 условных денежных единиц.