Аппроксимация как метод исследования числовых характеристик

Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем. Для вычисления значений сложных функций часто используется вычисление значения отрезка ряда, аппроксимирующего функцию. Аппроксимация также используется для обработки экспериментальных или натурных данных. На практике специалист чаще всего получает зависимости между исследуемыми параметрами экспериментально. В этом случае ставится натурный эксперимент, изменяются значения параметров на входе и выходе системы. Результаты измерений заносятся в таблицу. В результате проведения натурного эксперимента получается так называемая табличная функция [11].

При постановке задачи моделирования для определения значений функции в других точках, отличных от заданных табличных значений нужно заменить табличную функцию аналитической. Для этой цели используются методы аппроксимации и интерполяции.

Интерполяция – это замена исходной функции f(x) функцией φ(x) так, чтобы φ(x) точно проходила через точки исходной функции f(x). Интерполяция еще называется точечной аппроксимацией. Точки исходной функции f(x) называются узлами интерполяции.

Аппроксимация – это замена исходной функции f(x) функцией g (х) так, чтобы отклонение f(x) от g (х) в заданной области было наименьшим. Функция g (х) называется аппроксимирующей. Если исходная функция f(x) задана таблично (дискретным набором точек), то аппроксимация называется дискретной. Если исходная функция f(x) задана аналитически (на отрезке), то аппроксимация называется непрерывной или интегральной.

Аппроксимация или приближение – научный метод, позволяющий заменять одни объекты другими, в каком-то смысле близкими к исходным, но более простыми. Позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны) [2].

Следует рассматривать два случая:

1) аппроксимирующая функция ограничена диапазоном заданных точек и служит в качестве только интерполирующей зависимости, т.е. нахождения значений функций в точках внутри диапазона;

2) аппроксимирующая функция выступает в роли физического закона и с её помощью допускается экстраполировать переменные вне диапазона.

Для построения аппроксимирующей функции в Excel строится линия тренда с выводом коэффициента детерминации R² (величина достоверности аппроксимации). Линия тренда добавляется из контекстного меню кривой, построенной по точкам (функция f(x)) выбором пункта «Добавить линию тренда». В диалоговом окне «Линия тренда», вкладке «Тип» выбирается тип аппроксимирующей функции g (х), и устанавливаются флажки в полях «Показывать уравнение на диаграмме» и «Величина достоверности аппроксимации».

На графике появляется формула функции g (х) и значение R². Если значение R² близко к 1, то аппроксимирующая функция g (х) выбрана удачно, если не достаточно близко, то необходимо подобрать другую функцию.

Заметим также, что, если использовать в качестве линий тренда полиномы высоких степеней, то можно с точки зрения целевой задачи получить «абсурдный» результат прогноза, несмотря на высокое (близкое к 1) значение величины достоверности аппроксимации R². Иногда удается улучшить ситуацию заданием более точных коэффициентов (5-6 знаков после запятой) при установке для формулы на графике числового формата представления, но на внешних точках такая аппроксимация все равно выдаст недопустимые с точки зрения предметной области результаты.

 

Пример 2.1. Спрогнозируйте заданные таблично статистические данные (рис. 10) на последующие периоды времени.

Решение. Введем данные согласно рисунку только в столбцы А и В. На основе данных столбца А и столбца В построим точечную диаграмму со значениями, соединенными сглаживающими линиями.

В диалоговом окне «Линия тренда», вкладке «Тип» выберем линейную аппроксимацию, и установим флажки в полях «Показывать уравнение на диаграмме» и «Величина достоверности аппроксимации». Уравнение линии тренда имеет вид у = 67,833*х – 134411. Введем эту формулу в ячейку С2, где в качестве х сошлемся на ячейку, содержащую значение года (А2) (рис. 10).

Добавим еще одну линию тренда, щелкнув опять правой кнопкой мыши по линии графика и выбрав пункт добавления линии тренда. В диалоговом окне на вкладке «Тип» выберем логарифмическую аппроксимацию и установим флажки в полях «Показывать уравнение на диаграмме» и «Величина достоверности аппроксимации». Уравнение второй линии тренда имеет вид у=135801*Ln(х) – 1Е+06. Установим для формулы на графике числовой формат представления для более точного определения свободного члена и введем формулу в ячейку D2.

Рис. 10. Экстраполяция аппроксимирующей функции

Величина достоверности аппроксимации (R²) для обеих моделей составила 0,9745, она близка к 1, и это говорит о том, что и линейная, и логарифмическая аппроксимирующие функции достаточно точно описывают реальные данные.

Найдем отклонения для обеих аппроксимаций, как модуль разности между статистическими и теоретическими данными, т.е. для ячейки Е2 формула будет иметь вид: = ABS (C2-B2), для ячейки F2 – = ABS (D2-B2). Также найдем максимум отклонения в обоих случаях.

Пример 2.2. Пусть мы имеем табличную функцию, которая для нескольких значений x определяет соответствующие значения f(x):

Таблица 1.

x	f(x)
0	0
1	0,8415
2	0,9093
3	0,1411
4	−0,7568
5	−0,9589
6	−0,2794

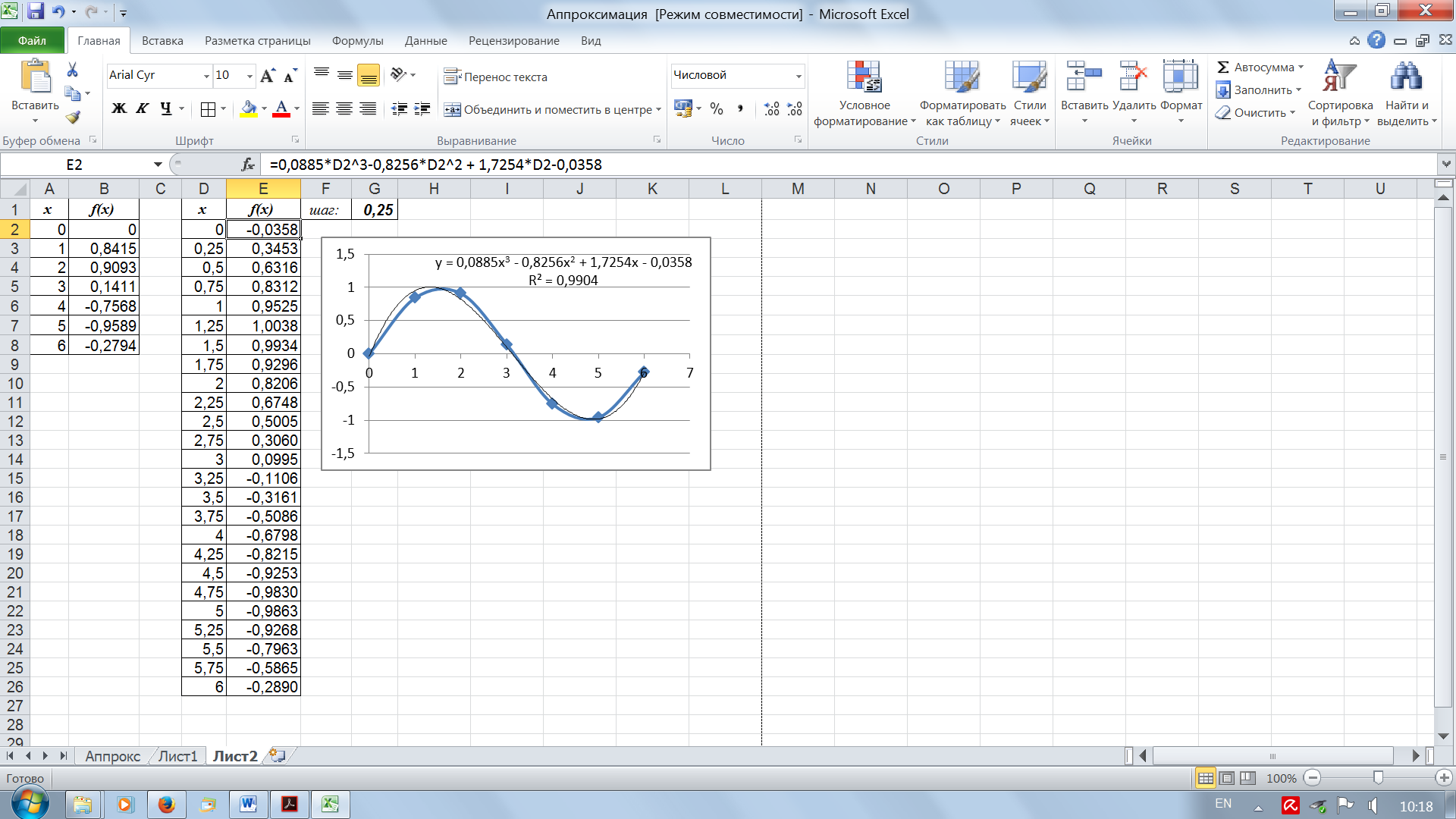
Требуется найти значение функции в точках x = 2,5 и x = 4,25.

Решение. Введем исходные данные на лист Excel. Дополнительно построим таблицу, где в качестве значений х будут числа от 0 до 6 с шагом 0,25. По данным первой таблицы построим точечную диаграмму и добавим на график линию тренда. В качестве аппроксимирующей кривой лучше всего выбрать полином 3 -й степени, что определяется из внешнего вида графика. Величина достоверности аппроксимации (R²) при этом составляет 0,99, а уравнение имеет вид: y = 0,0885 x ³ – 0,8256 x ² + 1,7254 x – 0,0358 (рис. 12).

Рис. 11. Интерполяция аппроксимирующей функции

Введем это уравнение в новую таблицу в ячейку Е2, где в качестве х укажем значение из ячейки D 2 и скопируем формулу в остальные ячейки. Из таблицы находим значения функции в искомых точках: при x=2,5 f(x) = 0,5005, при x=4,25 f(x) = - 0,8215.

Пример2.3. Торговая фирма по результатам реализации одного из видов товаров в течение нескольких периодов времени получила следующие экспериментальные данные (таблица 2). Найти равновесную цену.

Таблица 2.

№ периода	Цена (усл. ед.)	Спрос	Предложение
1	0,1	3	2
2	0,2	2,8	2,5
3	0,3	2,4	3,5
4	0,4	2,1	3,9
5	0,5	2	4,7
6	0,6	1,7	5,2

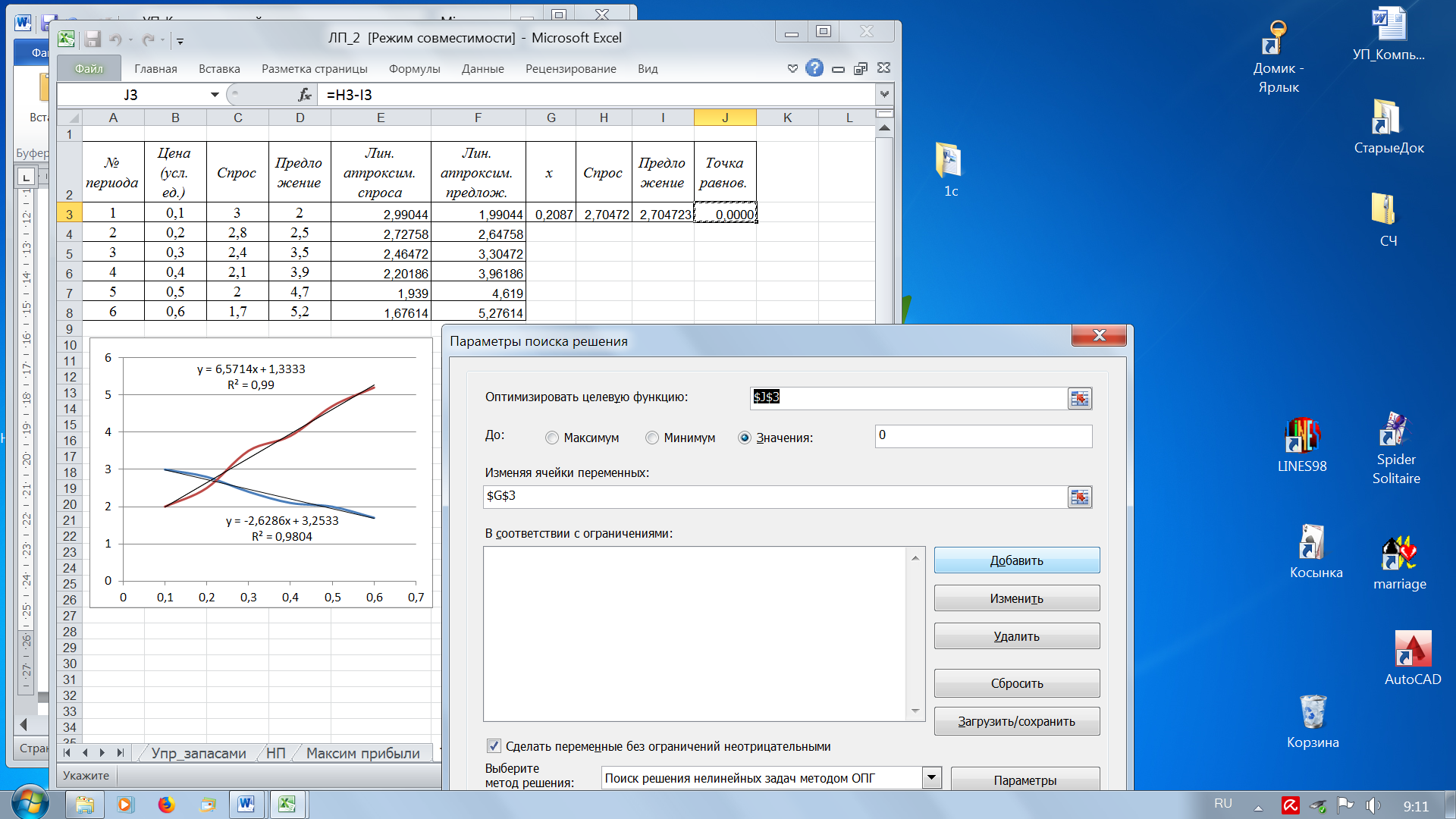
Решение. По условию задачи необходимо найти такую цену, при которой спрос будет равен предложению, или их разница будет равна 0. В графической интерпретации необходимо найти точку пересечения кривых спроса и предложения.

Введем исходные данные на лист Excel (рис. 12). Построим точечную диаграмму по столбцам В, С и D. Добавим столбцы для аппроксимирующих кривых (Е и F). Построим линии тренда отдельно для кривых спроса и предложения, выбрав в качестве аппроксимирующих кривых линейные функции (график на рисунке 13). В ячейки Е3 и F 3 введем уравнения:

  = -2,6286*B3 + 3,2533 и  = 6,5714*B3 + 1,3333 соответственно.

Рис. 12. Нахождение точки равновесия спроса и предложения

Из анализа исходных данных, а также построенных линий тренда очевидно, что равновесная цена находится в окрестности точки х=0,2. Введем это число 0,2 в ячейку G 3. В соседнюю ячейку Н3 введем уравнение аппроксимирующей функции для спроса, а в ячейку I 3 – уравнение аппроксимирующей функции для предложения. В ячейку J 3 введем разность между этими двумя ячейками и воспользуемся функцией Поиск решения. Решение представлено на рисунке 40. Равновесная цена равна 0,2087.

Пример 2.4. Зависимость затрат от объема производства задана приведенной ниже таблицей.

Таблица 3.

Объем производства	Затраты
1	2,7
1,2	3,2
1,4	3,7
1,6	4,1
1,8	4,7
2	5,1
2,2	5,6
2,4	5,8

 

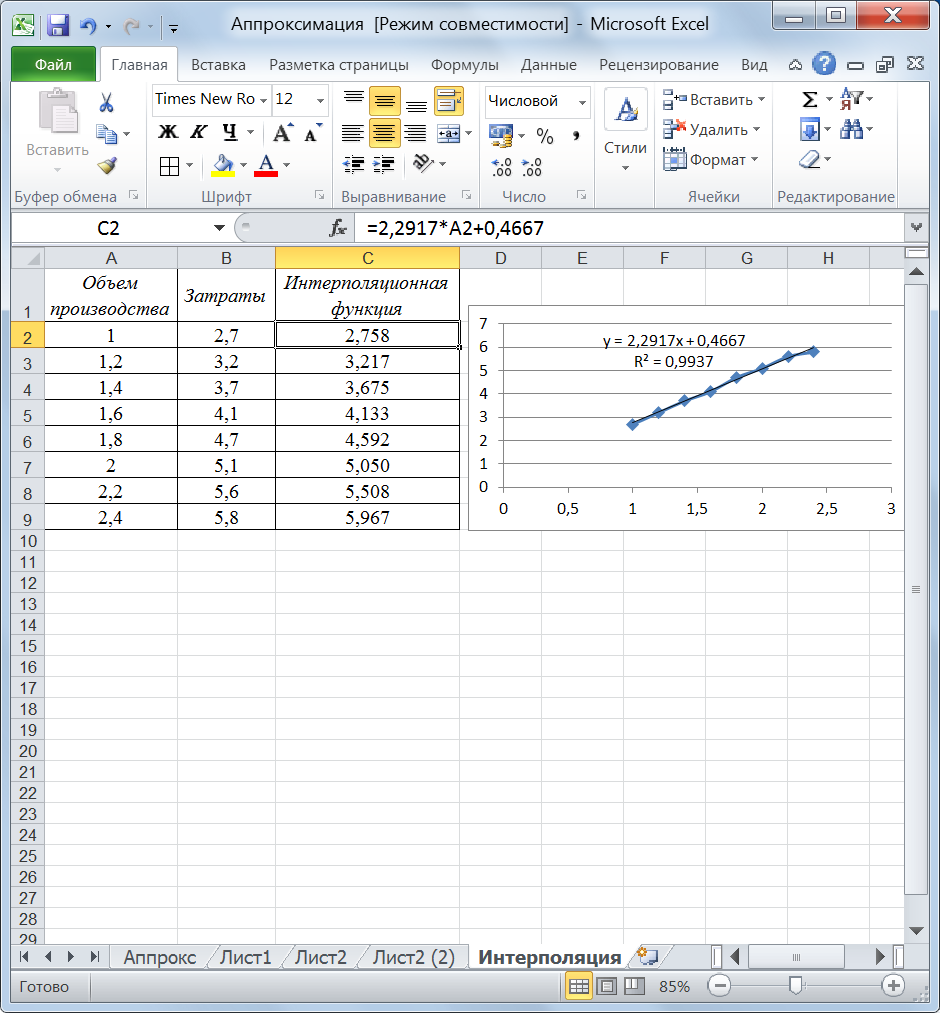
Требуется найти предельные издержки производства при объеме выпуска х=1,9.

Решение. В задаче функция зависимости затрат от объема производства задана не аналитически, а таблично. Поэтому, прежде всего, нужно получить аналитическую зависимость в виде интерполяционной функции и далее использовать ее для решения задачи (рис. 13).

Рис. 13. Аппроксимация табличных значений

 

Следующим шагом, имея аналитическую зависимость затрат об объема производства, вычислим производную этой функции. Для этого зададим некоторую окрестность точки х=1,9 (можно вставить строчки в таблицу), вычислим значения функции в этих точках и найдем отношение приращения функции к приращению аргумента (рис. 14).

Рис. 14. Решение задачи 2.4

 

Задания для самостоятельного выполнения

Задание 2.1. Введите статданные в таблицу и постройте аппроксимирующую кривую, где в качестве линии тренда выберите последовательно полиномы 2 -ой, 3 -ей и 4 -ой степени. Сравните полученные результаты. Какая аппроксимирующая функция наиболее подходит для прогнозирования данных на будущие периоды времени?

Таблица 4.

Год	Сумма страховых выплат	Аппроксимирую-щая функция 1	Аппроксимирую-щая функция 2	Аппроксимирую-щая функция 3
1999	150000
2000	200000
2001	300000
2002	450000
2003	450000
2004	420000
2005
2006
2007

 

Задание 2.2. По заданным таблично экспериментальным данным найдите значения функций в заданных точках.

Таблица 5.

Вариант 1		Вариант 2		Вариант 3		Вариант 4
x	f(x)	x	f(x)	x	f(x)	x	f(x)
0	6,2	0	-6,2	1	6,2	0	-6,2
1	2,22	1	-3,22	2	18,5	1	-3,22
2	-1,15	2	1,15	3	22,6	2	1,15
3	-3,2	3	3,2	4	24,55	3	3,2
4	-1,6	4	4,5	5	26,3	4	1,6
5	1,85	5	5,75	6	28,55	5	-2,65
6	5,65	6	8	7	30,1	6	-5,65
в точке:	3,5	в точке:	1,5	в точке:	4,5	в точке:	2,5

 

Задание 2.3. Допустим, спрос и предложение на компакт-диск знаменитой певицы представлены следующей таблицей:

Таблица 6.

№ периода	Цена (усл. ед.)	Спрос	Предложение
Сентябрь	1	19	221
Октябрь	2	56	154
Ноябрь	3	98	102
Декабрь	4	170	60
Январь	5	195	35

Найдите равновесную цену.