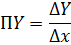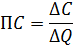Тема 3. Решение прикладных экономических задач: предельные величины в микроэкономике (4 час.)

Применение дифференциального исчисления к исследованию экономических процессов получило название предельного анализа.

В экономических задачах одни экономические показатели являются функциями каких-либо других показателей или величин. Иначе говоря, существует зависимость одних показателей от других – Y=f(x).

Так, например, себестоимость продукции зависит от производимого объема C=f(Q), издержки производства – зависят от количества выпускаемой продукции и т.п. Предельные экономические показатели характеризуют величину прироста величины функции ΔY от прироста ее аргумента Δx:

Так, например, предельная себестоимость характеризует себестоимость ΔС прироста продукции ΔQ:

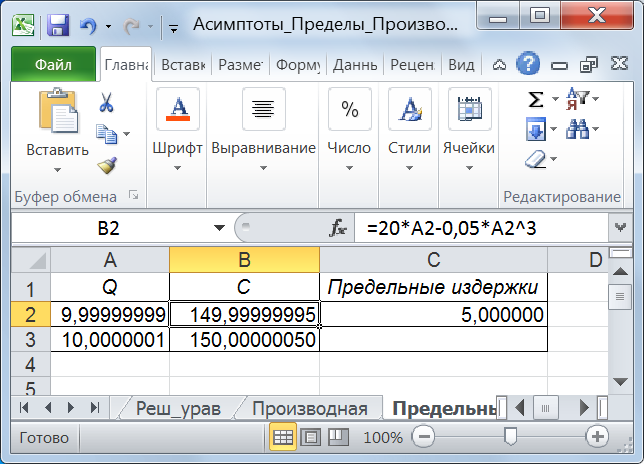
Если зависимость ΔY от Δx непрерывна, то приведенное разностное уравнение можно заменить производной ПY = f'(x).

Пример3.1. Пусть зависимость издержек производства от объема выпускаемой продукции в денежных единицах выражается формулой

C=20Q – 0,05Q³.

Требуется определить предельные издержки производства при объеме выпускаемой продукции 10 ден. ед.

Решение. Предполагая, что в ячейке А2 рабочего листа будет записано значение Q_k – левая граница окрестности точки Q =10, в ячейку В2 введем формулу = 20*А2 – 0,05*А2^3. Скопируем введенную формулу в ячейку В3 (рис. 15). В ячейку С3 введем формулу вычисления производной:

=(B3-B2)/(A3-A2).

В ячейки А2 и А3 введем значения Q для левой и правой окрестности, соответственно. После выполнения приведенных выше операций в ячейке С2 будет получен результат (рис. 15).

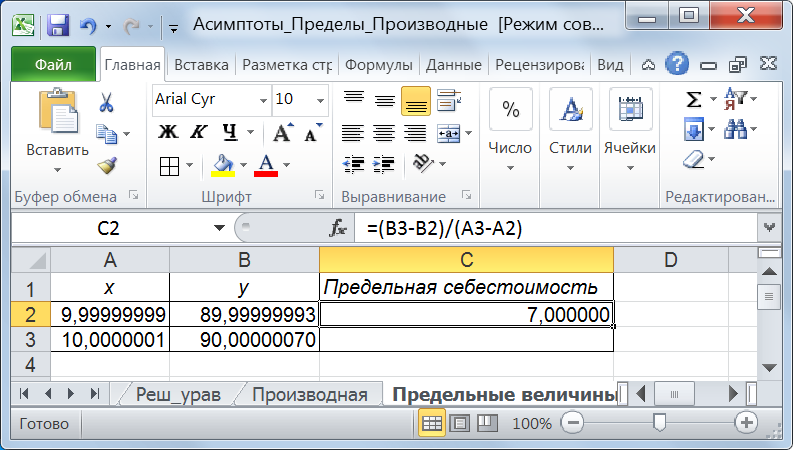
Рис. 15. Определение предельных издержек производства

Таким образом, предельные издержки производства при объеме выпускаемой продукции 10 ден.ед. составляют 5 ден. ед.

Пример3.2. Зависимость между себестоимостью единицы продукции y и объемом продукции x выражает формула y = 10x – 0,01x³. Найти предельную себестоимость при объеме продукции x = 10 единиц.

Определить целесообразность расширения производства.

Решение. Предельную себестоимость продукции характеризует производная функции себестоимости, демонстрирующая прирост функции при изменении аргумента на 1 единицу.

Искомая предельная себестоимость может быть определена в результате нахождения производной в точке x = 10.

В ячейки А2 и А3 введем значения x для левой и правой окрестности, соответственно. В ячейки В2 и В3 введем формулы, вычисляющие себестоимость единицы продукции, зависящие от объема продукции х. После вычисления производной в ячейке С2 будет получен результат (рис. 16).

Рис. 16. Определение предельных издержек производства

Значение предельной себестоимости при объеме продукции, равном 10 единиц, составляет 7 (ден. ед.).

Ответ: При сложившейся технологии производства, себестоимость выпуска 1 единицы продукции (при объеме производства 10 единиц) составляет 9 ден. ед. В то время как себестоимость единицы дополнительной продукции (одиннадцатой единицы) составляет 7 ден. ед., что свидетельствует о целесообразности расширения производства.