Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейное программирование и его применение в экономике
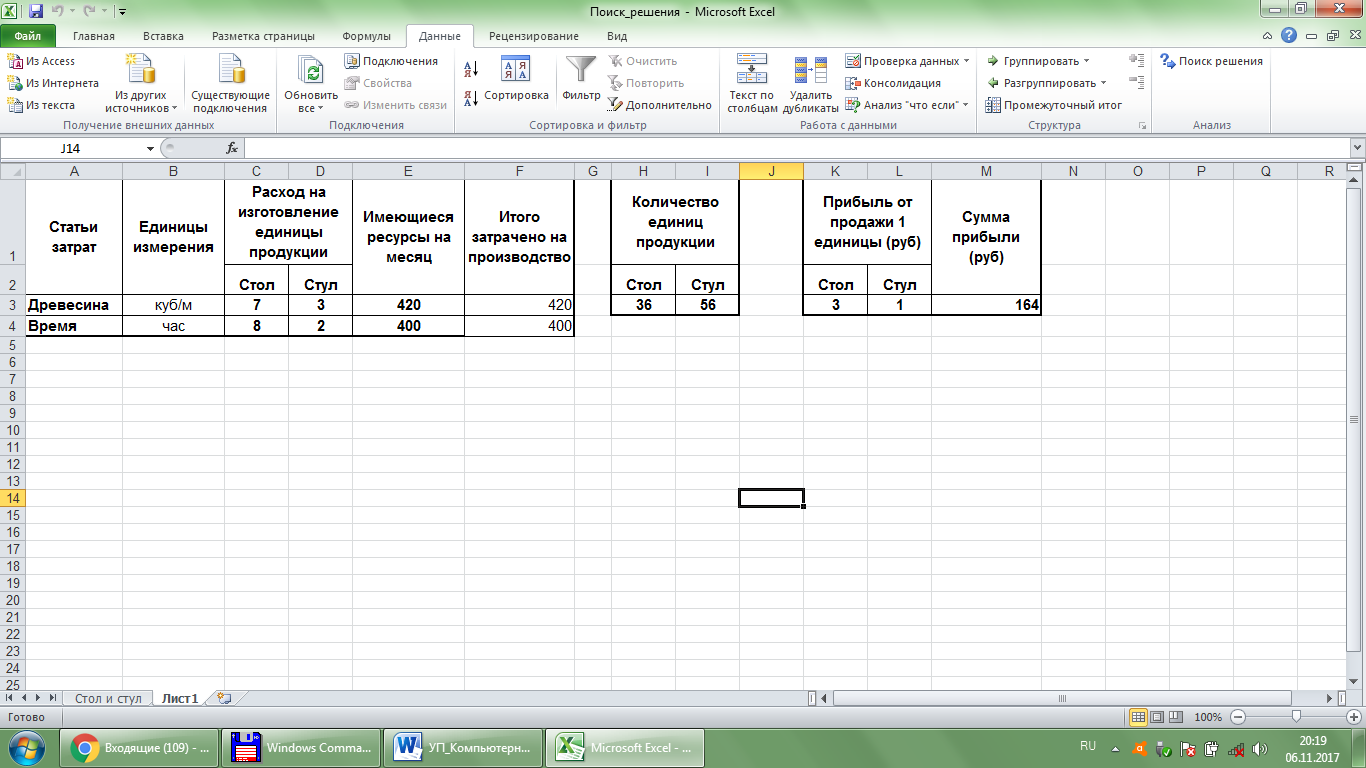
Задачи о распределении ресурсов. Имеется несколько ограниченных ресурсов для изготовления нескольких изделий, использующих эти ресурсы. Необходимо так спланировать производство изделий, чтобы получить максимальную прибыль. Задача о смесях. Имеется несколько ингредиентов, из которых составляются смеси в определенных пропорциях. Необходимо составить план приготовления смесей, чтобы прибыль от их продажи была максимальной. Задача о выборе оптимального меню. Имеется набор продуктов, обладающих некоторой калорийностью, а также известны количества белков, жиров и углеводов для каждого из этих продуктов и их стоимость. Требуется составить меню, удовлетворяющее требованиям калорийности и сбалансированности питательных продуктов, и при этом минимизирующее суммарную стоимость. Транспортная задача. Ее формулировка состоит в следующем: имеется несколько пунктов производства и пунктов потребления некоторого продукта. Для каждого из пунктов производства задан объем производства, а для каждого пункта потребления — объем потребления. Известна также стоимость перевозки из каждого пункта производства в каждый пункт потребления единицы продукта. Требуется составить план перевозок продукта, в котором все пункты потребления были бы обеспечены необходимыми продуктами, ни из какого пункта производства не вывозилось бы продуктов больше, чем там производится, а стоимость перевозки была бы минимальной. Задача о назначениях. Имеется несколько должностей и соответствующее количество претендентов на эти должности. Назначение i -того претендента на j -тую должность связано с затратами C[i,j]. Требуется распределить претендентов по должностям так, чтобы суммарные затраты были бы минимальны. Пример 6.1. Фирма производит два вида продукции: столы и стулья. Расход на изготовление единицы продукции дан в виде таблицы (рис. 34). Каждый стул приносит 1 руб. прибыли, а каждый стол – 3 руб. Сколько стульев и столов должна изготовить фирма, если она располагает 420 куб/м древесины и 400 часов рабочего времени и хочет получить максимальную прибыль?
Рис. 34. Исходные данные Решение. Определим переменные задачи (рис. 35), от которых будут зависеть величины затраченных ресурсов и будущей прибыли, это количество столов и количество стульев, которые изначально можно установить равными нулю (или 1, или любому другому значению), а далее в этих ячейках отобразится решение.
Рис. 35. Переменные задачи Определим целевую ячейку: она должна содержать формулу прибыли от продажи данного количества продукции (СУММПРОИЗВ(Н3: I 3; K 3: L 3)). Целевая функция, находящаяся в целевой ячейке обязательно должна ссылаться на изменяемые ячейки (рис. 36)!
Рис. 36. Целевая ячейка Далее определим функции ограничений. Фирма не может потратить ресурсов (в данном примере древесина и время) больше, чем у нее их имеется. Чтобы соблюсти это ограничение, необходимо рассчитать, а сколько же древесины и рабочего времени тратит фирма, выпуская такое количество изделий, которое находится сейчас в ячейках Н3:I3. Для этого в столбце «Итого затрачено на производство» надо найти сумму произведений количества каждого изделия на нормативный расход каждой статьи затрат. Ячейки «Итого затрачено на производство» должны содержать формулы, обязательно включающие в себя изменяемые ячейки (рис. 37)!
Рис. 37. Ячейки "Итого затрачено на производство" Далее вызовем инструмент «Поиск решения». Обычно он находится на вкладке Данные. Если он у вас отсутствует, необходимо подключить соответствующую надстройку следующими действиями: Файл / Параметры / Надстройки / Поиск решения, нажать кнопку Перейти и снова выбрать Поиск решения. Заполним окно поиска решения согласно рисунку 38. Получим решение, представленное на рисунке 39.
Рис. 38. Окно «Поиск решений»
Рис. 39. Решение задачи Пример 6.2. Распределение ресурсов. Продолжим решение задачи, представленное в примере 5.1. Фирма «Фасад» производит двери для продажи местным строительным компаниям. На фирме работает 10 рабочих в одну смену (8 рабочих часов), 5 дней в неделю, что дает 400 часов в неделю. Рабочее время поделено между двумя существенно различными технологическими процессами: собственно производством и конечной обработкой дверей. Из 400 рабочих часов в неделю 250 отведены под производство и 150 под конечную обработку. Вопрос задачи, сколько дверей различных типов нужно производить, чтобы максимизировать прибыль?
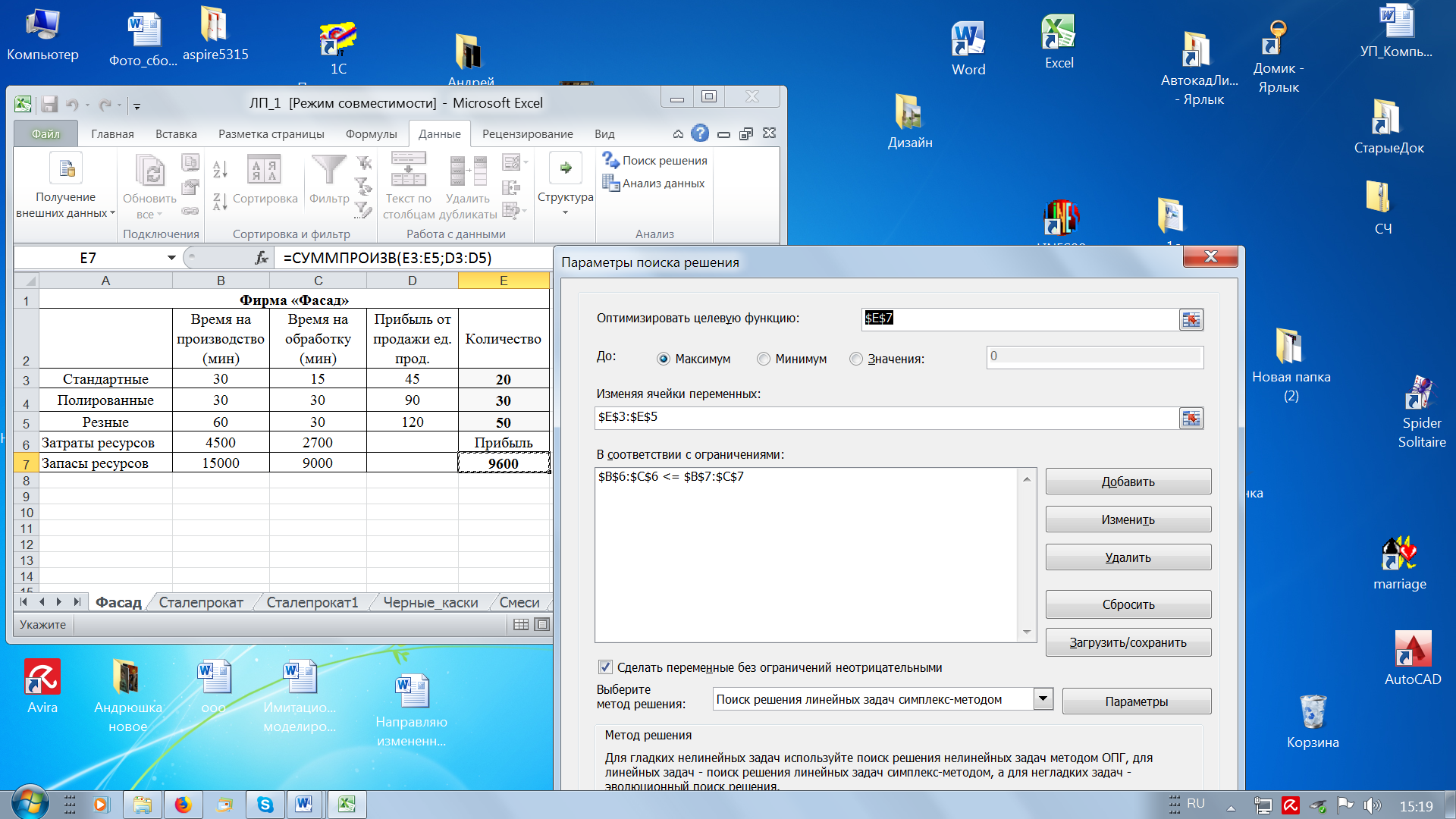
Решение. Прежде всего, определим цель задачи и вид целевой функции. В данном случае мы хотим максимизировать прибыль, следовательно, целевая функция должна вычислять полную прибыль. Полная прибыль у нас вычислена в ячейке Е7. Однако, в предыдущей задаче нам были заданы количества производимых дверей каждого типа, а здесь количества производства дверей каждого типа выступят в качестве переменных решения, т.е. ячейки Е3:Е5 станут изменяемыми ячейками. На следующем этапе решения следует выяснить, при каких ограничениях нужно найти максимальную прибыль. Из условия задачи следует, что можно затратить на производственную стадию не больше 250 часов в неделю, а на обработку не больше 150 часов. Внесем эти данные в ячейки В7 и С7 соответственно, но в минутах (по условию задачи t1<=250*60 (мин), а t2<=150*60 (мин)), это запасы временных ресурсов (рис. 40). Реальные затраты времени t1 и t2 рассчитываются в ячейках В6:С6 как сумма произведений норм расхода времени на количество выпускаемых изделий. Вызываем надстройку «Поиск решения» для определения оптимального по прибыли плана производства. Не забудем отметить, что задача соответствует линейной модели и что переменные неотрицательны. Больше никаких изменений здесь делать не нужно.
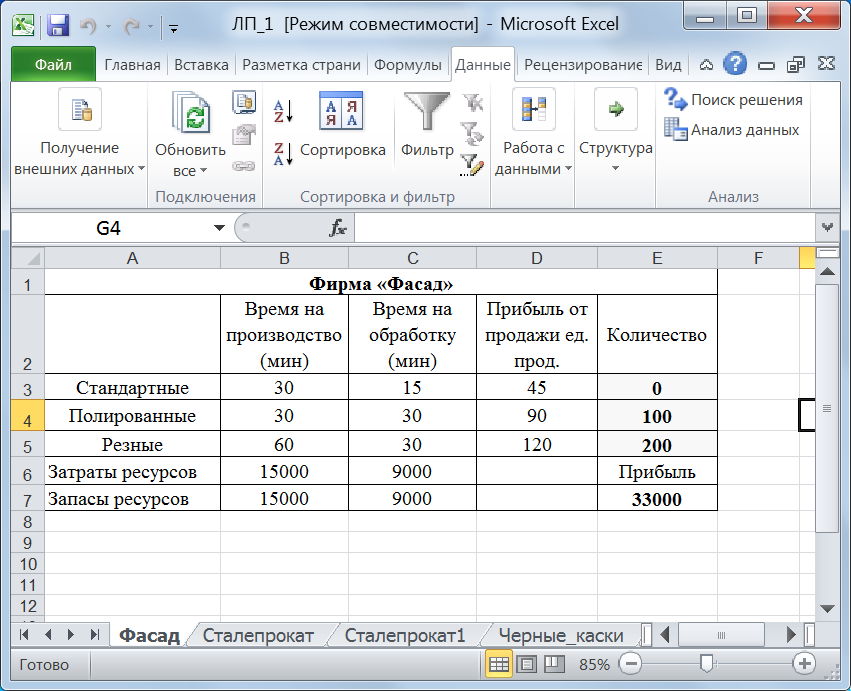
Рис. 40. Компьютерная модель задачи Сохраним найденное решение и проверим, что получился следующий результат (рис. 41).
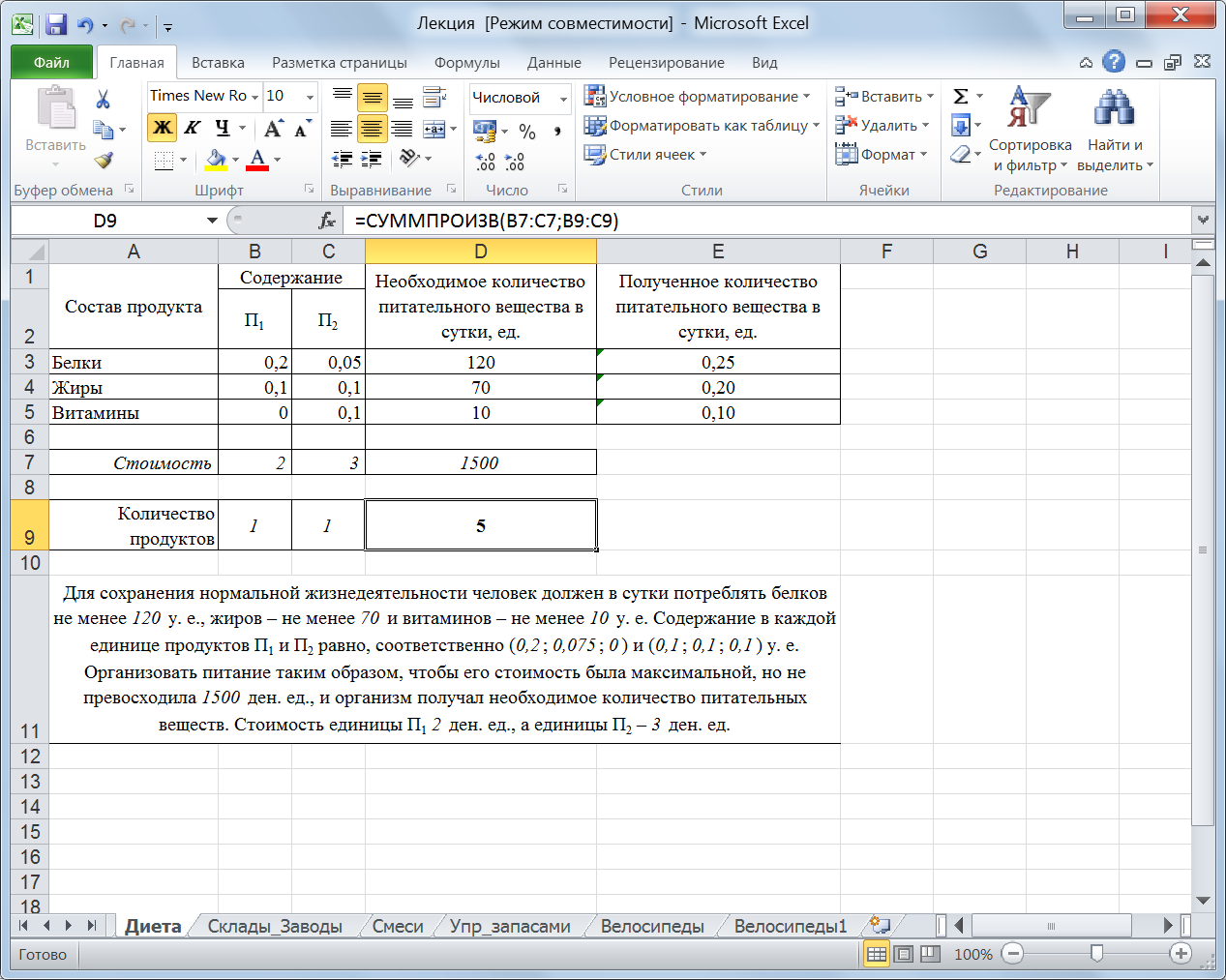
Рис. 41. Оптимальное решение задачи В данном случае оказывается, что максимально возможная прибыль равна 33000 $ и получена она будет, если производить за неделю 100 полированных дверей и 200 резных. Это и есть оптимальный план производства. Пример 6.3. О выборе оптимального меню. Для сохранения нормальной жизнедеятельности человек должен в сутки потреблять белков не менее 120 у. е., жиров – не менее 70 и витаминов – не менее 10 у. е. Содержание в каждой единице продуктов П1 и П2 равно, соответственно (0,2; 0,1; 0) и (0,05; 0,1; 0,1) у. е. Организовать питание таким образом, чтобы его стоимость была максимальной, но не превосходила 1500 ден. ед., и организм получал необходимое количество питательных веществ. Стоимость единицы П1 2 ден. ед., а единицы П2 – 3 ден. ед. Решение. Компьютерная модель задачи представлена на рисунке 42.
Рис. 42. Задача о выборе меню Переменные задачи – это количество продуктов П1 и П2. Полученное количество каждого питательного вещества в сутки вычисляется как сумма произведений количества каждого продукта (изначально положим количество равное единице) на соответствующее содержание данного вещества в продукте.
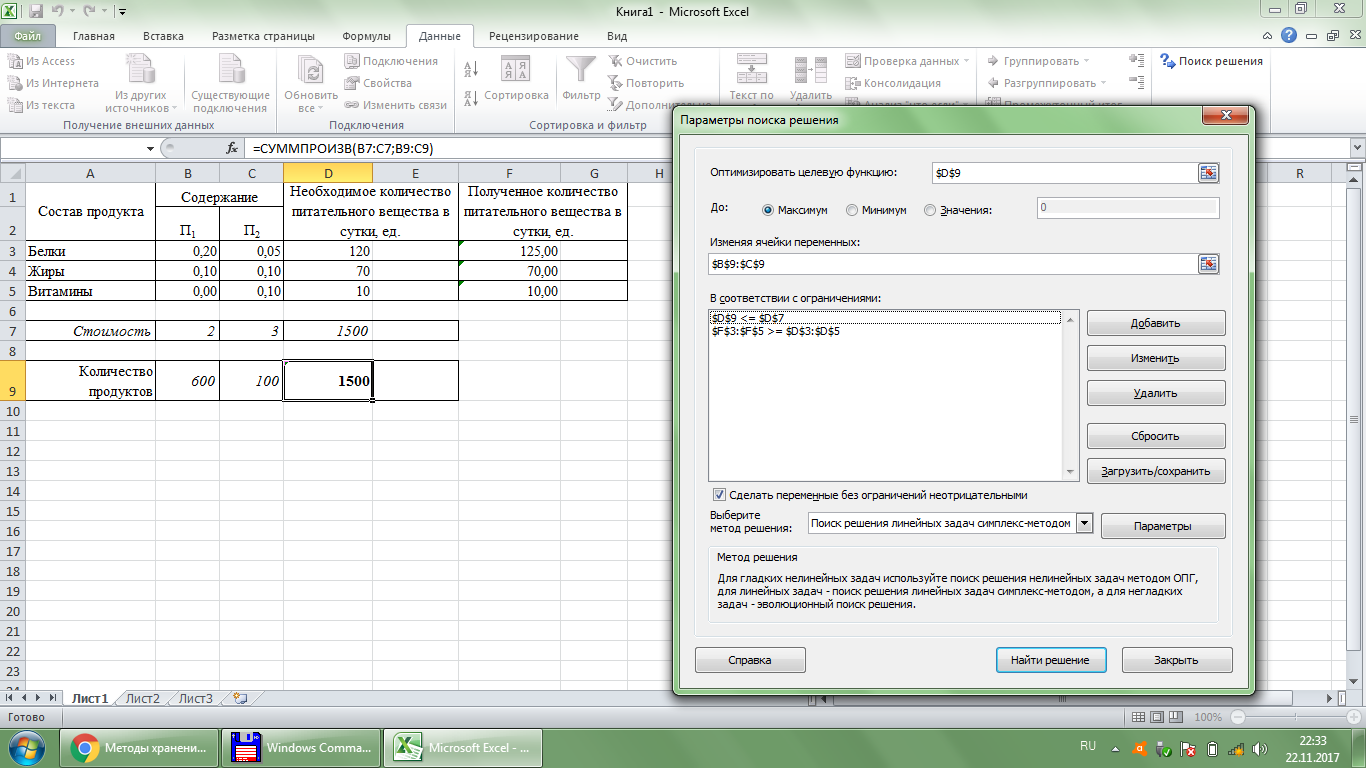
Рис. 43. Параметры поиска решения На целевую ячейку, вычисляющую общую стоимость набора продуктов, накладывается ограничение (см. рисунок 43). Ответ: 600 и 100 единиц продуктов П1 и П2 соответственно. Пример 6.4. Распределение ресурсов. Сталепрокатный завод производит стальные листы трех различных размеров: 100 дюймов, 80 дюймов и 55 дюймов. Поступил заказ на стальные листы размером 45, 30 и 18 дюймов в количестве 150, 200 и 185 штук соответственно. Каким образом компания должна разрезать стальные листы, чтобы минимизировать отходы? Решение. Переведем формулировку задачи на язык количественных методов. Из листов каждого из размеров (100, 80 и 55) можно выкроить по нескольку различных наборов заказанных листов. Например, из листа размера 55 дюймов можно получить 1 лист размером 45 дюймов (10 дюймов – в обрезки), или 1 лист в 30 дюймов и 1 в 18 дюймов (7 – в обрезки), или 3 листа в 18 дюймов (1 дюйм – в обрезки). Все возможные варианты раскроя приведены в таблице. Так как для каждого варианта известны и количество полученных листов, и количество обрезков, то в качестве переменных логично выбрать количество листов раскроенных по каждому из описанных вариантов.
Пример организации таблицы для расчета всех нужных для решения задачи величин приведен в таблице 15. Таблица 15.
Столбец Остаток рассчитывается как разница между размером листа проката (ячейка из столбца В, для первого варианта ячейка В3) и суммой произведений размеров листов (ячейки С2:Е2 для всех вариантов) на способ разрезки по данному варианту (ячейки С3:Е3 для первого варианта). Целевой функцией будет общее количество остатков (сумма произведений (встроенная функция СУММПРОИЗВ ()) числа разрезанных листов (диапазон F 3: F 17) на остаток для каждого типа разрезки (столбец G 3: G 17)). Цель – минимизация остатков при условии исполнения заказа. Для проверки условия исполнения заказа необходимо определить полученное количество листов каждого типа как сумму произведения числа разрезанных листов каждого типа (диапазон F 3: F 17) на количество листов каждого типа для каждого варианта разрезки (диапазон С3:С17 для размера листов в 45 дюймов, диапазон D 3: D 17 для размера в 30 дюймов, Е3:Е17 для размера в 18 дюймов). Данные для Поиска решения будут выглядеть очень просто: целевая ячейка – G 19, цель – минимум, изменяемые ячейки – F 3: F 17. По смыслу задачи следует потребовать, чтобы переменные были целыми числами (F 3: F 17 = целое). Как обычно во вкладке параметры отмечаем, что задача линейная и переменные неотрицательны. Условие выполнения заказа может быть записано по-разному. Можно потребовать точного выполнения заказа (C18:E18 = C19:E19), что, очевидно, соответствует недопустимости получения лишних листов заказанных размеров. Можно использовать более мягкое условие: количество полученных листов не менее заказанного (C18:E18 >= C19:E19), что допустимо в случае, когда оставшиеся листы могут быть проданы другому заказчику.
При ответе на вопрос разумно потребовать точного выполнения заказа. При этом общее количество остатков будет равняться 675 дюймам. Для выполнения заказа придется разрезать 44 листа по 3-ему варианту, 3 листа по 5-ому варианту, 106 листов по 8-му, 44 – по 10-му и 1 лист по 15-му варианту. Пример 6.5. О смесях. В настоящее время в магазине имеются запасы: сушеных бананов – 800 кг, сушеных абрикосов – 600, кокосовых кусочков – 500, изюма – 700, грецких орехов – 900 кг. Цены на товары указаны в таблице 16. Таблица 16.
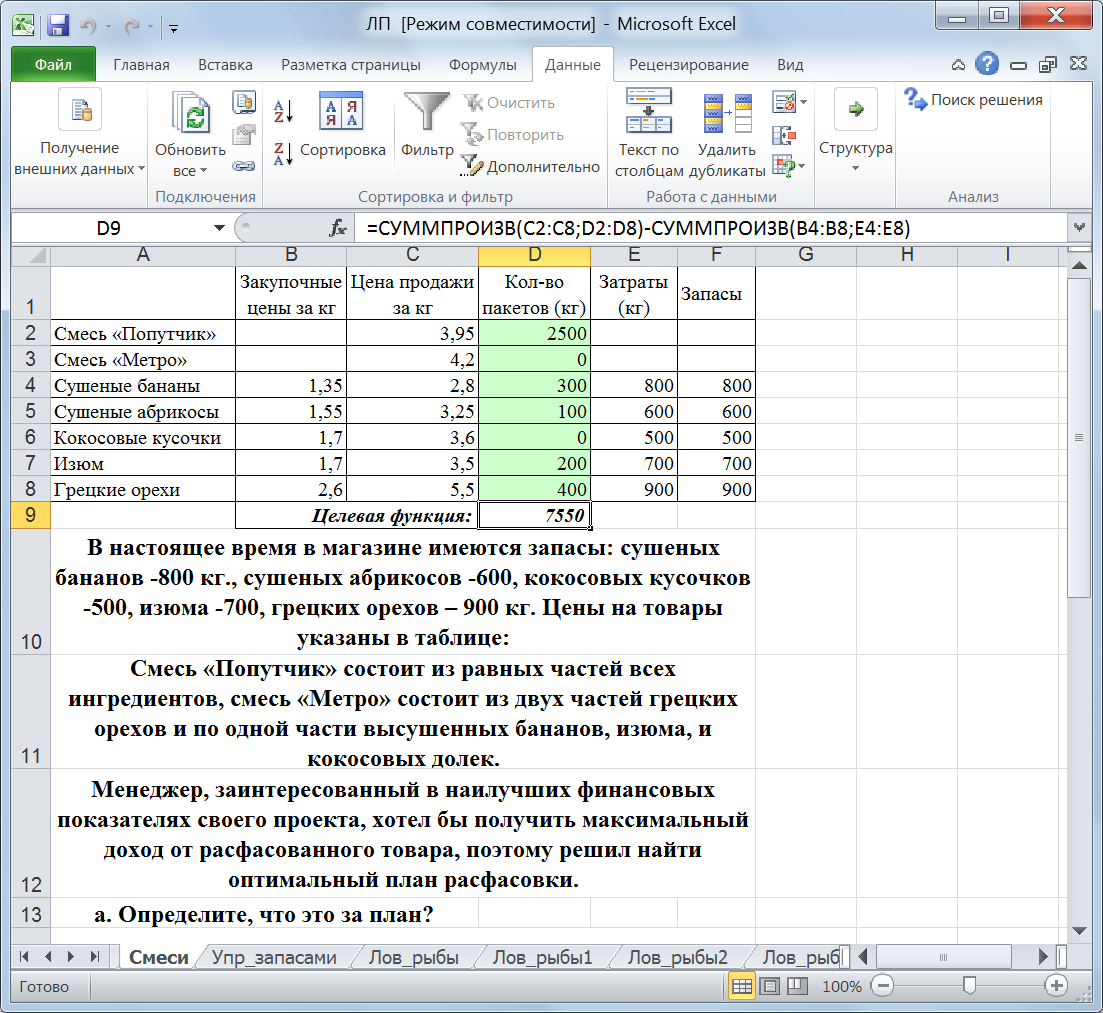
Смесь «Попутчик» состоит из равных частей всех ингредиентов, смесь «Метро» состоит из двух частей грецких орехов и по одной части высушенных бананов, изюма, и кокосовых долек. Менеджер, заинтересованный в наилучших финансовых показателях своего проекта, хотел бы получить максимальный доход от расфасованного товара, поэтому решил найти оптимальный план расфасовки. Определите этот план. Решение. Компьютерная модель задачи представлена на рисунке 44.
Рис. 44. Компьютерная модель задачи о смесях В модели цветом выделены изменяемые ячейки – количество пакетов расфасовки. Затраты ингредиентов рассчитываются как сумма произведений доли каждого ингредиента в смеси на количество пакетов этой смеси (например, сушеные бананы входят в смесь «Попутчик» с коэффициентом 0,2, в смесь «Метро» с коэффициентом 0,2, а в расфасовку «Сушеные бананы» с коэффициентом 1). Затраты ингредиентов не должны превышать их запасы. Целевая функция – это доход от продажи расфасованных пакетов, он рассчитывается по следующей формуле: =СУММПРОИЗВ(C2:C8;D2:D8)-СУММПРОИЗВ(B4:B8;E4:E8) – прибыль от продажи товара минус затраты на ингредиенты. После поиска решения план расфасовки будет таким (рис. 45).
Рис. 45. Решение задачи о смесях Пример 6.6. Транспортная задача. Корпорация «Современные железобетонные изделия» имеет в окрестностях и черте города 5 небольших заводов ЖБИ (ЖБИ 1, ЖБИ 2, …, ЖБИ 5). Кроме этого, у корпорации есть 3 охраняемых площадки-склада (Склад 1, Склад 2, Склад 3) для временного хранения изделий, хотя корпорация старается работать на заказ. В настоящий момент в отделе продаж имеется заказ от строительной фирмы на поставку ж\б блоков в количестве 1050 шт. Заводы могут за обусловленный срок поставить следующее количество блоков:
Корпорация имеет транспортный отдел, который доставляет заказанные блоки на площадки семи клиентов строительной компании. Стоимости перевозок с заводов клиентам и с заводов на склады даны в таблицах 17 и 18: Таблица 17.
Таблица 18.
Строительная компания заказывает поставку блоков в два этапа: через 2 недели 545 блоков и еще через две недели 505 блоков. Заказы для отдельных клиентов приведены в таблице 19: Таблица 19.
Но корпорации выгодней выполнить весь заказ в течение 3-4 дней, а затем переналадить оборудование на изготовление другого изделия из пакета заказов. В этом случае приходится часть изделий отправлять клиентам немедленно после набора необходимой прочности, а остальные размещать на собственных складах. Разумеется, в этом случае в обусловленные заказом сроки 505 складированных блоков должны будут доставлены клиентам прямо со складов. Стоимости перевозок блоков со складов к клиентам даны в следующей таблице:
Составьте план перевозок заводы-клиенты, заводы-склады и склады- клиенты так, чтобы издержки корпорации были минимальны. Учтите, что изготовленные заранее 505 блоков, реально можно складировать следующим образом: Склад A – 150 шт., Склад B – 150 шт. и Склад C – 205 шт. Оптимизируйте задачу по частям: сначала перевозки заводы-клиенты, затем заводы-склады, затем склады- клиенты. Решение. Начнем с перевозок «заводы-клиенты». Заводы представят к перевозке 1050 блоков, из которых к клиентам можно будет перевезти 545 блоков, а остальные придется везти на склады. Для нас это означает, что первая из отдельных задач не сбалансирована. Для того, чтобы сбалансировать задачу придется добавить фиктивного клиента «склад», который и «закажет» лишние 505 блоков. В этом случае задачу можно построить следующим образом (рис. 46).
Рис. 46. Перевозки «Заводы-клиенты» Целевая функция – полные издержки перевозки. Выражения для задания ограничений в надстройке " Поиске решения " записываются как обычно, строка B16:I16 сравнивается со строкой B8:I8, а столбец J11:J15 со столбцом J3:J7. Перевозку блоков к фиктивному клиенту мы оставляем бесплатной. Соответствующие издержки будут учтены при решении задачи о перевозке на склады. Поиск решения выдает следующий оптимальный план (рис. 47).
Рис. 47. План перевозок «Заводы-клиенты» Как мы видим, на склады отправится вся продукция завода ЖБИ 1 и часть продукции заводов ЖБИ 3 и ЖБИ 4. Стоимость этой фазы перевозок 15555 единиц. Следующая часть перевозок – перевозки с заводов на склады. В предыдущей части мы выяснили, сколько блоков должно быть вывезено на склады с каждого из заводов. Емкость складов и цены перевозки нам известны из условия задачи. Составим соответствующую таблицу (Рис. 48).
Рис. 48. Перевозки «Заводы-склады» В данном случае задача сбалансирована, так как емкость складов равна 505 блокам. Поиск решения дает следующий результат (рис. 49).
Рис. 49. План перевозок «Заводы-склады» Стоимость перевозок составила 17790 единиц. И последняя часть задачи – перевозки с трех складов клиентам, которые происходят через две недели. Задача и здесь сбалансирована, второй заказ в сумме составляет 505 блоков, которые мы ранее запасли на трех складских площадках. Составляем новую таблицу (рис. 50) и найдем решение последней, третьей задачи.
Рис. 50. Перевозки «Склады-клиенты» Полученное решение представлено на рис. 51.
Рис. 51. План перевозок «Склады-клиенты» Издержки по перевозкам составили 15210 единиц. Суммируя результаты, получаем, что минимальные издержки при оптимизации перевозок по частям составят 48555 единиц.
Пример 6.7. О назначениях. Постановка задачи. Институт получил гранты на выполнение четырех исследовательских проектов. Выходные результаты для первого проекта являются входными данными ля второго проекта, выходные данные для второго проекта – это входные данные для третьего проекта, выходные результаты третьего проекта используются для работы над четвертым проектом. В качестве научных руководителей проектов рассматриваются кандидатуры четырех ученых, обладающих различным опытом и способностями. Каждый ученый оценил время, необходимое ему для работы над проектом. Таблица необходимого времени (в месяцах): Таблица 20.
Требуется выбрать научного руководителя для каждого из проектов, так чтобы суммарное время для выполнения всех проектов было минимальным. Такая задача является задачей о назначениях. В общем виде следующая формулировка: имеется n работ и n кандидатов для их выполнения. Затраты i – того кандидата на выполнение j – той работы равны cij (i, j = 1, …,n). Каждый кандидат может быть назначен на одну работу и каждая работа может быть выполнена только одним кандидатом. Требуется найти назначения кандидатов на работы, при котором суммарные затраты на выполнение работ минимальны. Математическая модель. Пусть xij – переменные, значения которых равно 1, если i – ый кандидат выполняет j – тую работу, и 0 в противоположном случае: Условие, что один кандидат выполняет только одну работу, выглядит так:
Условие о том, что каждая работа может выполняться только 1 кандидатом:
Целевая функция:
Задачу о назначениях можно рассматривать, как транспортную задачу, в которой претенденты это «исходные пункты», а вакансии – «пункты назначения», cij имеет смысл «стоимости перевозки». Решение. Построим компьютерную модель решения задачи (см. рисунок 52). Матрица распределения ученых по проектам будет содержать двоичные значения: 0 – ученый не занят в данном проекте, 1 – данный ученый занят в данном проекте. При этом необходимо контролировать суммы чисел по столбцам и по строкам, введя соответствующие ограничения, для выполнения (1) и (2) условий задачи. Ответ: Оптимальное время для выполнения всех проектов = 17 (мес.).
Рис. 52. Компьютерная модель решения задачи
Задания для самостоятельного выполнения Задание 6.1. Фирма производит два вида продукции: столы и стулья. Расход ДСП на изготовление одного стола – 4 кв.м, одного стула – 0,5 кв. м; рабочего времени: на изготовление одного стола – 6 час, одного стула – 2 час. Каждый стул стоит 600 руб., а каждый стол – 1500 руб. Сколько стульев и столов должна изготовить фирма, если она располагает 600 кв.м ДСП и 420 часов рабочего времени и хочет получить максимальную прибыль? Задание 6.2. Каждому животному нужно ежедневно выдать не менее 6 единиц белков, 8 единиц жиров и 12 единиц углеводов. Есть два вида корма. Одна единица первого корма содержит 21 единицу белка, 2 единицы жира, 4 единицы углеводов и стоит 30 руб. Для второго корма соответствующие цифры следующие: 3, 2, 2 и 2. Составьте математическую модель и найдите оптимальный рацион питания.
Задание 6.3. Предположим, что мы решили производить два вида объективов А и В. Объектив вида А состоит из 3-х линзовых компонентов, вид В – из 4-х.За неделю можно изготовить не более1800 линз. На сборку объектива вида А требуется – 15 минут, вида В – 30 минут. Рабочая неделя для 4 сотрудников составляет160 часов. Сколько объективов А и В надо изготовить, чтобы получить максимальную прибыль, если объектив вида А стоит 3500 рублей, вида В – 4800 рублей.
Задание 6.4. В ресторане готовятся фирменные блюда трех видов (блюдо А, блюдо В и блюдо С) с использованием при приготовлении ингредиентов трех видов (ингредиент 1, ингредиент 2 и ингредиент 3). Расход ингредиентов в граммах на блюдо задается следующей таблицей: Таблица 21.
Стоимость приготовления блюд одинакова(100 руб.). Ежедневно в ресторан поступает 5 кг ингредиента 1 и по 4 кг ингредиентов видов 2 и 3. Каково оптимальное соотношение дневного производства блюд различного вида, если производственные мощности ресторана позволяют использовать весь запас поступивших продуктов?
Задание 6.5. В школе проводится конкурс на лучшую стенгазету. Одному школьнику дано следующее поручение. Купить акварельной краски по цене 30 ден. ед. за коробку, цветные карандаши по цене 20 ден. ед. за коробку, линейки по цене 12 ден. ед., блокноты по цене 10 ден. ед.. Красок нужно купить не менее трех коробок, блокнотов – столько, сколько коробок карандашей и красок вместе, линеек не более пяти. На покупки выделяется не более 300 ден. ед. В каком количестве школьник должен купить указанные предметы, чтобы общее число предметов было наибольшим? Задание 6.6. Существует правило, согласно которому коммерческие банки должны покупать в определённой пропорции ликвидные активы – ценные бумаги, чтобы компенсировать неликвидность кредитов. В нашем примере ликвидное ограничение таково: ценные бумаги должны составлять не менее 30% средств, размещённых в кредитах и ценных бумагах. Собственные средства банка в сумме с депозитами составляют 100 млн. долл. Часть этих средств, но не менее 35 млн. долл. должна быть размещена в кредитах, остальная в ценных бумагах. Определить объём денежных средств, размещённых в кредитах и ценных бумагах, если их доходность составляет 10%, 15% соответственно.
Задание 6.7. Штат научно-исследовательской лаборатории (НИЛ) должен состоять из: 5 лаборантов, 8 инженеров, 11 младших научных сотрудников (м.н.с.), 3 старших научных сотрудников (с.н.с.), 2 ведущих научных сотрудников, и заведующего НИЛ. Общий месячный фонд зарплаты составляет 400 тыс. руб. Необходимо определить, какими должны быть оклады сотрудников НИЛ при условии, что оклад лаборанта не должен быть меньше прожиточного минимума 6 тыс. руб. и: инженер получает в 1,8 раза больше лаборанта, при этом на 600 руб. больше лаборанта; м.н.с. не меньше, чем в 1,8 раза больше лаборанта, при этом на 1100 руб. больше инженера; с.н.с. в 3,5 раза больше лаборанта; ведущий научный сотрудник не меньше, чем в 3,2 раза больше лаборанта, при этом на 3200 руб. больше с.н.с.; заведующий НИЛ в 5 раз больше лаборанта.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 840; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.182.45 (0.112 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






 .
.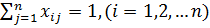 (1).
(1). (2).
(2).