Определение непотопляемости.

Определение остойчивости.

 

Stability

 

Определение плавучести.

 

Floatability

 

 

Определение непотопляемости.

 

 

Определение общей и местной прочности.

 

Определение управляемости, устойчивости на курсе и поворотливости

Устойчивость на курсе - это способность судна сохранять направление прямолинейного движения.

Поворотливость - способность судна изменять направление движения и описывать траекторию заданной кривизны.

 

Определение ходкости.

 

 

Типы диаграмм дифферентов.

Types of trim diagram

Диаграмма осадок носом и кормой

Эта диаграмма именуемая также диаграммой дифферентов, служит для оперативного решения различных эксплуатационных задач при посадке судна прямо и с дифферентом. Существует несколько видов таких диаграмм. Рассмотрим построение и использование одного из наиболее удобных ее вариантов.

Наметим на масштабе Бонжана ряд равноотстоящих осадок носом и кормой, перекрывающих весь желаемый диапозон посадок. Фиксируя какое-либо значение Тн, проведем через точку на кормовом перпендикуляре, и для каждой из них найдем водоизмещение V и его статический момент относительно миделя Vx . По полученным значениям нанесем точки, откладывая по вертикальной оси D= V, а по горизонтльной – статический момент M = Vx при стандартном значении плотности . Полученные точки определяют кривую, все точки которой соответствуют посадкам судна с одной и той же осадкой носом Тн. Поступая таким же образом со всеми намеченными значениями Тн и Тк. Получим сетку кривых постоянных значений осадок носом и кормой, определяющих посадку судна. Вместе с тем, прямоуголные координаты D и М точек определяют нагрузку судна, если приближенно положить х х , пренебрегая в первом из уравнений равновесия (2.10) выражением (z - z )tg как малой величиной при обычных дифферентах. Т.о. диаграмма дифферентов (рис. 2.19) представляет собой наложенные друг на друга две системы координат: прямоугольную с осями D и M , определяющую нагрузку судна, и криволинейную с линиями Тн и Тк, определяющую посадку судна.

Рассмотрим решение некоторых практических задач с помощью диаграммы дифферентов.

По составленному грузовому плану рассчитана нагрузка судна: водоизмещение D и статический момент водоизмещения относительно миделя M =D х . Определить посадку судна. Откладывая по вертикальной оси диаграммы водоизмещение, а по горизонтальной – момент, находим точку, изображающую нагрузку судна. Пользуясь сеткой кривых Тн и Тк, по найденной точке, при необходимости интерполируя между кривыми, прочитываем осадки носом и кормой для расчетного состояния нагрузки. Обратная задача (по заданной посадке Тн и Тк определить водоизмещение D и момент M ) решается в обратном порядке: по Тн и Тк определяем точку на диаграмме, по которой прочитывается D и M .

Определить посадку судна после приема груза массой m с абсциссой центра тяжести x . Точку, изображающую первоначальную нагрузку или соответствующую первоначальную посадку, смещаем по вертикали вверх на величину m и по горизонтали на величину mx вправо, если она положительна, или влево,если она отрицательна. По полученной новой точке прочитываем новую осадку по кривым Тн и Тк.

Перенос груза по длине судна. Судно имеет посадку, определяемую осадками Тн и Тк Тн, т.е. с дифферентом на корму. Определить сколько балласта надо перекатать из ахтерпика в форпик, расстояние между которыми (измеренное между их центрами тяжести) равно l, чтобы посадить судно на ровный киль. По осадкам Тн и Тк находим на диаграмме изображающую точку. Так как при перекате балласта водоизмещение судна меняться не буде, изображающая точка будет перемещаться только по горизонтали и ее надо переместить до линии нулевого дифферента. Прочитав для этой точки момент М ’, а также момент M для первоначальной точки, найдем момент M = M’ - M , который надо создать перемещением балласта, и определим массу балласта m = M /l.

Определить массу и абсциссу центра тяжести принятого груза, если до его приема осадки были Тн и Тк, а после приема стали Тн1 и Тк1. По осадкам находим водоизмещение D и момент М до приема груза и D и М после приема, откуда определяем массу груза m = D - D и абсциссу его центра тяжести

 

Требования и критерии начальной остойчивости Кодекса ИМО

Requirements and criteria regarding initial stability

Остойчивость при малых углах наклонения – начальная остойчивость.

 

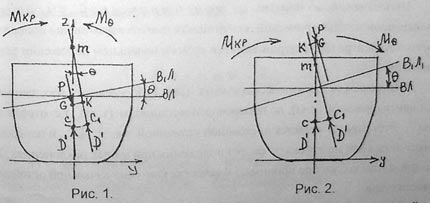
Пара сил, образованная весом судна и силой поддержания, стремящаяся возвратить судно в первоначальное положение равновесия, называется восстанавливающей парой, а момент этой пары - восстанавливающим моментом Mθ.

Метацентрической высоты: поперечной метацентрической высотой называется возвышение поперечного метацентра над центром тяжести судна в начальном положении равновесия.

Метацентр – центр кривизны траектории по которой перемещается центр величиныв процессе наклонения.

Центр величины – точка приложения равнодействующих сил поддержания, действующих на судно (центр погруженной части корпуса)

Центр тяжести – точка приложения равнодействующих сил тяжести, действующих на судно.

Метацентрический радиус – определяется расстоянием от метацентра до центра величины.

Поперечная мегацентрическая высота (рис. 1) определяется расстоянием от центра тяжести (т. G), до поперечного метацентра (т. m), т.е. отрезком mG. Этот отрезок является постоянной величиной, т.к. и Ц.Т.,и поперечный метацентр не изменяют своего положения при малых наклонениях. В связи с этим его удобно принимать в качестве критерия начальной остойчивости судна.
Если поперечный метацентр будет находиться выше центра тяжести судна, то поперечная метацентрическая высота считается положительной. Тогда условие остойчивости судна можно дать в следующей формулировке: Судно остойчиво, если его поперечная метацентрическая высота положительна. Чтобы установить, какими данными необходимо располагать для получения значения поперечной метацентрической высоты, обратимся к рис. 4, на котором показано относительное расположение центра величины С, центра тяжести G и поперечного метацентра m судна, имеющего положительную начальную поперечную остойчивость. Из рисунка видно, что поперечная метацентрическая высота h может быть определена по одной из следующих формул:

h = Zm – ZG, где Zm = r+Zc

М = P*l = D*g*h*sin - метацентрическая формула остойчивости

Требования и критерии Кодекса ИМО, регламентирующие характеристики ДСО.

Площадь под положительной частью ДСО:

А30°≥0,055 м*рад

А40°≥0,09 м*рад

А30-40≥0,03 м*рад

Максимальное плечо ДСО:

Lmaх≥0,25м для судов длинной ≤85

Lmaх≥0,2м для судов длинной ≥ 105м (максимальное восстанавливающие плечо)

Максимальный угол крена: Ө≥30°(Ө≥25)

Закат диаграммы: Өv≥60

Исправлення метац.высота h≥0.15m

Критерий погоды K=b/a≥1

Максимальное востанавливавающие плечо должно проходить под углом крена не менее чем 25°

 

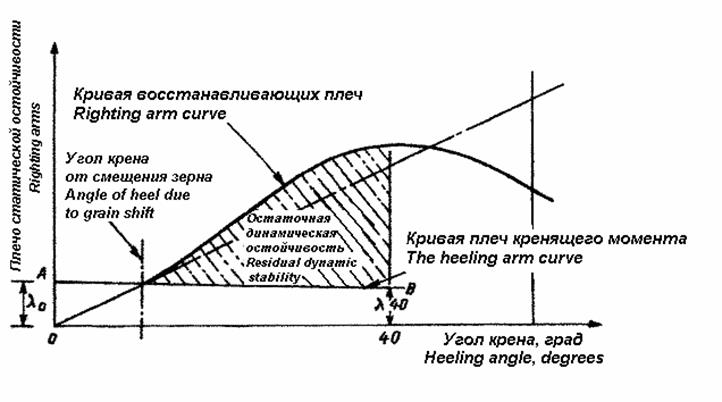
Международный Кодекс по безопасной перевозке зерна насыпью. Требования к остойчивости.

International Code for the safe carriage of grain in bulk Stability Requirements

 

1. начальная метацентрическая высота, после коррекции для свободных поверхностных эффектов жидкостей в резервуарах, должна быть не менее 0,3 м.

2. Угол крена из-за смещения зерна не должен быть больше 12° или угол, при котором кромка палубы погружается, в зависимости от того, что меньше.

3.Аост≥0,075

 

INTERNATIONAL CODE

FOR THE SAFE CARRIAGE OF GRAIN IN BULK

RESOLUTION MSC.23(59)

(adopted on 23 May 1991)

 

 

 

Закон Фруда.

Конкретно закона нет! только такое

Число Фруда

Если помните, говоря о скорости судна, мы акцентировали ваше внимание на слове «относительная».

Дело в том, что скорость переходного режима каждого судна различна и напрямую зависит от его эффективной длины (обычно – длины по ватерлинии). Английский физик Уильям Фруд (1810–1879) подметил это, наблюдая за снующими по Темзе баржами (тогда – на лошадиной тяге). И не только подметил, но и вывел формулу, описывающую характер образуемых судном волн в зависимости от его длины и скорости:

Fr=v/√gl

Где:

v – скорость судна, м/с;

g – ускорение свободного падения, 9,81м/с2;

Lwl – длина судна по КВЛ, м;

Fr – число Фруда.

 

«Числа Фруда» описывают режим волнообразования для судов разного размера. Так, буксируя стократно уменьшенную модель в 10 раз медленнее реального судна, увидим такие же волны, как и у прототипа – только в масштабе 1:100.

Но что же числа Фруда означают практически? А вот что:

 

вплоть до Fr = 0,4 – водоизмещающий режим (при Fr = 0,4 судно начинает «карабкаться» на собственную носовую волну);

Fr = 0,5 – волновое сопротивление максимально; диапазон переходного режима Fr = 0,4…0,8;

при Fr = 1,0-1,2 – начало глиссирования, при котором судно поддерживается на поверхности как силой Архимеда, так и набирающей со скоростью удельный вес гидродинамической составляющей;

Fr = 1,5 – начало чистого глиссирования (судно поддерживается только гидродинамическими силами).

Водоизмещающее судно рассчитывают так, чтобы оно двигалось в диапазоне чисел Фруда до 0,2-0,3; для малых глиссирующих Fr≥2-3. Важная оговорка: граничные значения Фруда, отвечающие переходам одного режима в другой, весьма условны, так как зависят от формы погружённой части корпуса. Поэтому применять их для определения минимальной скорости воднолыжника или выхода судна на подводные крылья нельзя – на этот счёт есть формулы посложнее. Более того: для описания глиссирующего режима специалисты чаще оперируют не вышеописанным Fr (или FrL – по длине), а FrV (по водоизмещению), ибо в гидродинамическом режиме поддержания водоизмещение «важнее» длины...

Однако оставим тонкости профессионалам. А сами посчитаем абсолютные скорости входа и выхода из переходного режима для конкретно вашей лодки (по формуле выше). Лень считать – найдите «свою» пару цифр (в км/ч или узлах – как больше нравится) в таблице (напоминаю: для входа в неё нужна длина по КВЛ, а не габаритная!). Запомните их или нанесите метками на циферблат стрелочного лага (это нагляднее). А теперь главное: избегайте двигаться в диапазоне скоростей МЕЖДУ ними (т.е., в переходном режиме)

Уравнения качки судна

Motion equations

θm = α0 / (1 - σ2 / nθ2). Так как σ = 2π/τ, а nθ = 2π / Tθ,

то θm = α0 / (1 - Tθ2 / τ2) или θm/ α0 = 1 / (1 - Tθ2 / τ2) (1),

где θm - амплитуда качки;

α0 - наибольший угол волнового склона;

Tθ - период собственных колебаний судна;

τ - период волны.

 

Из уравнения следует, что по мере приближения периода волны τ к периоду собственных колебании Tθ относительная амплитуда вынужденных колебаний возрастает и при отсутствии сил сопротивления воды становится бесконечно большой (при τ - Tθ). Такое явление называется резонансом.

В действительности, резонанс, хотя и не приводит к возникновению бесконечно больших амплитуд, вызывает появление резонансных максимальных амплитуд. Из сравнения кривых, приведенных на рисунке видно, что влияние сопротивления воды на относительную амплитуду вынужденных колебаний существенно лишь в том случае, когда отношение периодов находится в интервале 0,70 ≤ Tθ / τ ≤ 1,3; вне этой области влияние сопротивления незначительно.

Рассматриваемый случай качки является наиболее опасным. Если судно не обладает достаточной динамической остойчивостыо, то резонанс может привести к потере остойчивости и к опрокидыванию судна. Именно поэтому при нормировании остойчивости морских судов оценивают углы, возникающие не только от действия динамически приложенного давления ветра, но и углы крена при бортовой качке, исходя из предположения, что судно находится на регулярном волнении в условиях резонанса при положении лагом к волне.

 

 

Определение остойчивости.

 

Stability

 

Определение плавучести.

 

Floatability

 

 

Определение непотопляемости.