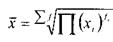Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительные статистические показатели, форма выражения, виды и расчет.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Относительный показатель представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками соц.-эк. процессов и явлений. При расчете относительного показателя абсолютный показатель, находящийся в числителе, называется текущим (сравниваемым),а показатель, который находится в знаменателе - основанием или базой. Относительные показатели могут выражаться в коэффициентах, процентах или промиле (в 1000 раз) 1) Относительный показатель динамики (ОПД) -это отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом.
ОПД показывает во сколько раз текущий уровень превышает предшествующий или какую долю от последнего составляет. Если данный показатель выражен кратным отношением, он называется коэффициентом роста, при домножении этого коэффициента на 100% получают темп роста. 2) Относительный показатель выполнения плана (ОПВП) используется предприятиями с целью перспективного планирования своей деятельности. ОПВП = фактический пок. данного вр * 100% Фактический пок. этого же периода 3) Относительный показатель структуры (ОПСтр) представляет собой соотношение структурных частей изучаемого объекта и их целого.
4) Относительный показатель координации (ОПК) — характеризует соотношение отдельных частей целого между собой.
При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной 5) Относительный показатель интенсивности (ОПИ)- характеризует степень распространения изучаемого процесса или явления в присущей ему среде: ОПИ = изучаемый пок *100% Другой пок. но связанный с 1м по смыслу 6)Относительный показатель сравнения (ОПС)
7) Относительный пок планового задания ОППЗ = плановый пок буд вр *100% Факт. пок данного периода 8) Относ пок рентабельности ОП рент = прибыль *100% выручка (затраты, капитал,...) 9) плотность населения = Кол-во населения / тер-я Сущность и значение средних показателей, средняя арифметическая, другие виды средних величин. Средняя величина представляет собой обобщенную количественную характеристику статистической совокупности в конкретных условиях места и времени. Сущность средней состоит в том, что она отражает типичный уровень признака и абстрагируется от индивидуальных особенностей, присущих отдельным единицам. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Средняя арифметическая и ее свойства. Наиболее распространенным видом средних величин является средняя арифметическая, которая в зависимости от характера имеющихся данных может быть простой или взвешенной. Средняя арифметическая простая применяется, когда значение вариантов встречается по одному числу раз.
Средняя арифметическая взвешенная применяется, когда отдельное значение признака повторяется неодинаковое количество раз, т.е. она используется в расчетах средней по сгруппированным данным или вариационным рядам.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений переходят о интервалов к их серединам. Другие виды средних. 3.1. Средняя гармоническая ~ это величина, обратная средней арифметической, Когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение, применяется формула средней гармонической взвешенной:
Когда объемы явлений, т.е. произведения (m, = m,). по каждому признаку равны, применяется средняя гармоническая простая
3.2. Средняя геометрическая - это величина, используемая как средняя из отношений или в рядах распределения, представленных в виде геометрической прогрессии Средняя геометрическая используется в расчетах среднегодовых темпов роста и для определения равноудаленной величины от минимального и максимального значений признака.
√ (Хn / n)
Средняя квадратическая Средняя квадратическая взвешанная
средняя хронологическая
|
|||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |



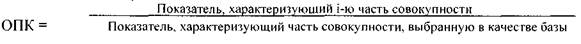


 f- частота/ веса - как часто встречается в той или иной вар-те.
f- частота/ веса - как часто встречается в той или иной вар-те.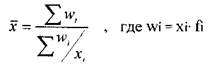 вместо w- m= х*F
вместо w- m= х*F
 средняя геометрическая: X= n-1
средняя геометрическая: X= n-1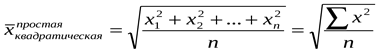
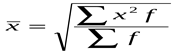
 если данные выражены моментным рядом чисел (особенность! складывать эти числа нельзя)
если данные выражены моментным рядом чисел (особенность! складывать эти числа нельзя)