
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 3. Тема «плоское движение твердого тела»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Поскольку задача 4 относится к теме «Плоское движение твердого тела» [1, 127-130, 132], скорость ползуна для данного положения механизма можно вычислить с помощью мгновенного центра скоростей шатуна. Для этого необходимо знать скорость какой-нибудь точки шатуна (например точки А) и направление скорости ползуна. Ускорение ползуна в данный момент времени можно найти с помощью векторной формулы распределения ускорений точек плоской фигуры, спроектировав ее на два взаимно перпендикулярных направления. В качестве полюса удобно принять точку А. Условие. Кривошип ОА длиной R вращается вокруг неподвижной оси О с постоянной угловой скоростью w и приводит в движение шатун АВ длиной Схемы механизмов приведены на рис. 9, а необходимые для расчета данные – в табл. 7.
Рис. 6. Схемы к задаче 4 Таблица 7
Примечание. Если при заданных значениях углов окажется, что шатун АВ перпендикулярен направляющим ползуна (см. рис. 9, схемы 1, 6), то значение угла b следует принять равным 15°. Пример решения задачи 3 Условие. Кривошип ОА длиной R=64 см вращается вокруг неподвижной оси О с постоянной угловой скоростью w=1 рад /с и приводит в движение шатун АВ длиной Решение: 1. Определим скорость точки А кривошипа как вращательную вокруг неподвижной точки О по соотношению Рис. 7 Рассмотрим движение шатуна в данный момент времени как вращательное относительно оси, проходящей через мгновенный центр скоростей РАВ перпендикулярно неподвижной плоскости, по отношению к которой происходит плоское движение. Угловая скорость шатуна АВ в этом случае определяется из соотношения
Модули скоростей точек В и С как вращательные – из соотношений
Расстояния АРАВ, BPАВ и СРАВ определим путем рассмотрения треугольников АВРАВ и АСРАВ, применив теоремы синусов и косинусов. Для заданного положения механизма получим
откуда
Подставив найденные значения расстояний в соответствующие формулы, получим
Вектор Направления скоростей показаны на рис. 10, б. 2. Для определения ускорений точек B, С и углового ускорения звена АВ воспользуемся векторным равенством, выбрав за полюс точку А, ускорение которой известно по величине и направлению:
где Ускорение точки А кривошипа в общем случае складывается из центростремительной
Вектор ускорения точки А направлен к центру вращения звена О (рис. 10, в). Центростремительное ускорение точки В определяется по формуле
Вектор Что касается ускорения точки В – Зададимся произвольно их направлениями по указанным линиям (см. рис. 10, в) и спроектируем уравнение (1) на оси координат. Знак в ответе покажет, соответствует ли истинное направление вектора принятому при расчете. Выбрав направления осей х и у, как показано на рис. 10, в, получаем
Из уравнения (2) находим
Направление ускорения Из уравнения (3) получаем
Знак «минус» показывает, что истинное направление Ускорение Угловое ускорение шатуна АВ с учетом того, что здесь
Вычисляя, находим
Направление ускорения 3. Для определения ускорения точки С воспользуемся векторным уравнением
Вращательное и центростремительное ускорения точки С во вращательном движении звена АВ вокруг полюса А определяются следующим образом:
Вектор Ускорение точки С находим, проектируя уравнение (4) на оси координат (см. рис. 10, в):
Полное ускорение точки С
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 и ползун В. Для заданного положения механизма найти скорости и ускорения ползуна В и точки С, а также угловую скорость и угловое ускорение звена, которому эта точка принадлежит.
и ползун В. Для заданного положения механизма найти скорости и ускорения ползуна В и точки С, а также угловую скорость и угловое ускорение звена, которому эта точка принадлежит.






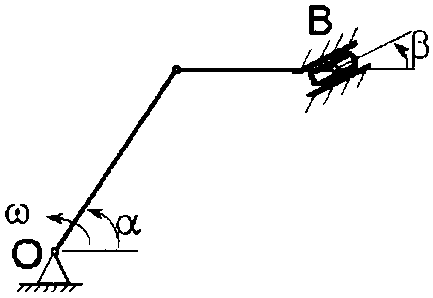


 . Скорость точки А перпендикулярна кривошипу ОА. Для определения скорости точки В найдем положение мгновенного центра скоростейРАВ шатуна АВ, для чего покажем направление скоростей точек А и В (скорость ползуна В имеет вектор по направляющим n – n), а затем из точек А и В восстановим перпендикуляры к скоростям vA и vB. Мгновенный центр скоростей РАВ шатуна АВ находится на пересечении этих перпендикуляров (рис. 10, б).
. Скорость точки А перпендикулярна кривошипу ОА. Для определения скорости точки В найдем положение мгновенного центра скоростейРАВ шатуна АВ, для чего покажем направление скоростей точек А и В (скорость ползуна В имеет вектор по направляющим n – n), а затем из точек А и В восстановим перпендикуляры к скоростям vA и vB. Мгновенный центр скоростей РАВ шатуна АВ находится на пересечении этих перпендикуляров (рис. 10, б). .
. ;
; .
. ,
,


 ;
; ;
; .
. направлен перпендикулярно отрезку СРAB в сторону, соответствующую направлению вращения звена АВ.
направлен перпендикулярно отрезку СРAB в сторону, соответствующую направлению вращения звена АВ. , (1)
, (1) – ускорение ползуна В;
– ускорение ползуна В;  – ускорение точки А, выбранной за полюс;
– ускорение точки А, выбранной за полюс;  – центростремительное (осестремительное, нормальное) ускорение точки В при ее вращении вокруг полюса А;
– центростремительное (осестремительное, нормальное) ускорение точки В при ее вращении вокруг полюса А;  – вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А.
– вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А. и вращательной составляющих
и вращательной составляющих 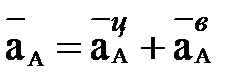 . Поскольку по условию кривошип ОА вращается равномерно, то
. Поскольку по условию кривошип ОА вращается равномерно, то  и ускорение точки А состоит только из центростремительной составляющей, модуль которой определяется по формуле
и ускорение точки А состоит только из центростремительной составляющей, модуль которой определяется по формуле .
. .
. ; (2)
; (2) . (3)
. (3)
 .
. .
. .
.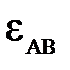 . Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращении звена совпадает с направлением его вращения, а при замедленном – противоположно ему. В данном случае угловое ускорение совпадает с направлением вращения шатуна.
. Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращении звена совпадает с направлением его вращения, а при замедленном – противоположно ему. В данном случае угловое ускорение совпадает с направлением вращения шатуна. ;
; .
. перпендикулярен вектору
перпендикулярен вектору  и направлен соответственно угловому ускорению
и направлен соответственно угловому ускорению  ;
; .
.



