
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа по теоретической механикеСодержание книги
Поиск на нашем сайте КОНТРОЛЬНАЯ РАБОТА ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ Статика При решении задач статики рекомендуется придерживаться такой последовательности [1, с.41-45]: 1) изобразить тело, равновесие которого исследуется, на чертеже; 2) приложить к нему все активные (заданные) силы; 3) определить виды связей, наложенных на рассматриваемое тело, и, используя принцип освобождаемости от связей, заменить их действие на тело соответствующими реакциями; отразить эти реакции на чертеже; направления реакций выбираются при этом произвольно; 4) провести оси координат; желательно оси располагать так, чтобы они пересекали как можно больше неизвестных сил или были к ним перпендикулярны; 5) определить вид полученной системы сил, действующих на рассматриваемое тело (с учетом активных сил и реакций), и составить соответствующие уравнения равновесия; 6) определить из полученных уравнений равновесия искомые величины и проанализировать полученные результаты. Задача 1. Тема «Плоская система сил» Задача 1 – на равновесие твердого тела (бруса) c осью в виде ломаной линии, находящегося под действием плоской системы сил, линии действия которых расположены как угодно в одной плоскости. При вычислении момента силы Р относительно выбранной точки удобно применить теорему Вариньона о моменте равнодействующей [2, с.87]. Для этого силу нужно разложить на две составляющие по горизонтальному и вертикальному направлениям, а затем найти момент силы Р относительно точки как сумму моментов этих составляющих относительно той же точки. Равномерно распределенная нагрузка характеризуется интенсивностью нагрузки (силой, приходящейся на единицу длины) и обозначается обычно буквой q. Равнодействующая распределенной нагрузки в общем случае равна площади эпюры нагрузки и приложена в центре тяжести этой площади [3]. Исходные данные приведены в табл. 1. Таблица 1
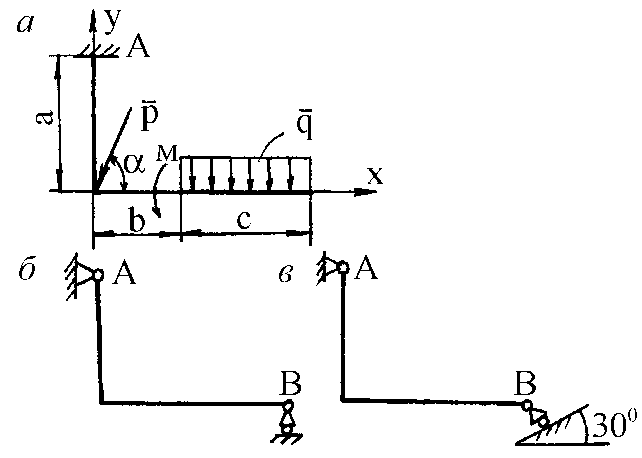
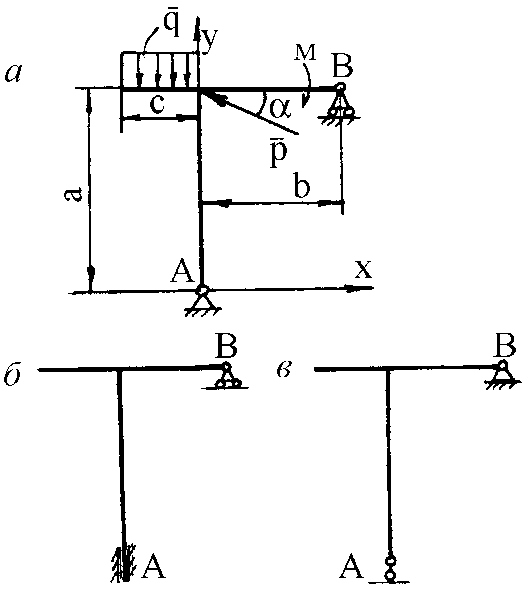
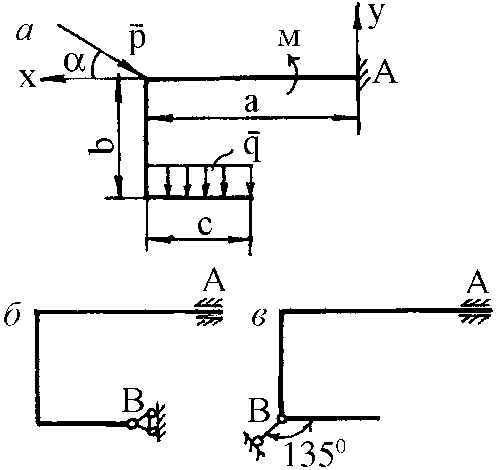
Условие. На схемах (рис. 1) показаны три способа закрепления бруса, ось которого – ломаная линия. Задаваемая нагрузка (см. табл. 1) и размеры (м) во всех трех случаях одинаковы. Определить реакции опор для того способа закрепления бруса, при котором реакция, указанная в табл. 1, имеет наименьший модуль.
Рис. 1. Схемы к задаче 1
Рис. 1. Окончание Пример решения задачи 1 Условие. Определить реакции опор для того способа закрепления бруса (рис. 2), при котором реакция – момент МА в заделке – имеет наименьшее значение. Дано: Р = 5 кН, М = 10 кН×м, q = 2 кН/м, a = 60°, а = 4 м, b = 2 м, с = 1 м.
Рис. 2 Решение. Рассмотрим систему уравновешивающихся сил, приложенных к конструкции. Равномерно распределенную нагрузку интенсивностью Q = q×в = 4 кН. Выбираем оси координат, изображая их на чертеже (рис. 3). Действие связей на конструкцию заменяем их реакциями (см. рис. 3): в схеме а: RAx, RAy, MA; в схеме б: Рис. 3 Для решения задачи на равновесие тела, находящегося под действием плоской системы сил, используются в общем случае три уравнения равновесия. Для определения наименьшего значения момента МА найдем его величину для всех трех схем, не определяя пока остальных реакций, т. е. используем одно уравнение равновесия. Силу Р разложим на две составляющие (Рx = Р×sin60°, Рy= P×cos60°) и найдем момент этой силы как сумму моментов ее составляющих. Для схемы а
Откуда
Для схемы б рациональнее составить уравнение равновесия относительно точки D – точки пересечения неизвестных реакций
Вычисления дают
Для схемы в составим уравнение равновесия моментов относительно точки Е, где пересекаются линии действия неизвестных реакций RВ и
откуда
Таким образом, наименьшее по модулю значение момента MA получается при закреплении бруса по схеме б. Определим остальные опорные реакции для этой схемы, используя для этого оставшиеся два уравнения равновесия:
Знак «минус» у найденной реакции Проверим правильность решения задачи, для чего составим уравнение равновесия моментов относительно, например, точки К:
Подставим в это уравнение найденные значения 4×1+6,5×1+10 – 3,18 – 4,33×4 = 0. Следовательно, задача решена верно. Результаты расчета сводим в таблицу (табл. 2). Таблица 2
Пример решения задачи 2 Условие. На горизонтальный вал насажено колесо радиусом r1 = 12 см и прикреплен перпендикулярно оси вала рычаг СD длиной Решение. К валу кроме силы Р, действующей на рычаг СD, приложена реакция веревки (сила натяжения) T, численно равная силе тяжести груза F, так как, по условию задачи, трения в блоке нет (рис. 5, а). Направлена эта реакция вдоль веревки в ту сторону, куда веревка тянет блок. Реакции подшипников RA и RB, расположенные в плоскостях, перпендикулярных оси Аy, разложим на взаимно перпендикулярные составляющие RAx, RAz, RBx и RBz. Направление составляющих выбирается произвольно.
Рис. 5 Составим уравнения равновесия для вала, находящегося под действием произвольной пространственной системы сил, пять из которых – RAx, RAz, RBx, RBz и Р, – неизвестны по модулю. Для этого необходимо сделать вид с положительного направления координатных осей, например с оси Ay (рис. 5, б).
Из последнего соотношения найдем
Из соотношения (5) определим
Из соотношения (4) вычислим
Из соотношения (3) найдем
Из соотношения (1) выводим
Знак «минус» перед значениями реакций RAz и RBx показывает, что эти реакции направлены противоположно указанным на рисунке. Условие равновесия (2) обращается в тождество, так как проекции на ось y всех сил рассматриваемой системы равны нулю. Для проверки правильности решения составим дополнительные контрольные уравнения равновесия моментов относительно осей x1 и z1, проходящих через точку В:
Подставив значения найденных реакций в эти уравнения, получим: 474×1,8+500×0,5×1,0–424,3×2,6 = 0; 240,6×1,8–500×cos30°×1,0 = 0. Контрольные уравнения обращаются в тождества, что свидетельствует о правильности полученных ответов. Модули реакций подшипников:
Результаты расчета сводим в таблицу (табл. 4). Таблица 4
Кинематика Пример решения задачи 3 Условие. Кривошип ОА длиной R=64 см вращается вокруг неподвижной оси О с постоянной угловой скоростью w=1 рад /с и приводит в движение шатун АВ длиной Решение: 1. Определим скорость точки А кривошипа как вращательную вокруг неподвижной точки О по соотношению Рис. 7 Рассмотрим движение шатуна в данный момент времени как вращательное относительно оси, проходящей через мгновенный центр скоростей РАВ перпендикулярно неподвижной плоскости, по отношению к которой происходит плоское движение. Угловая скорость шатуна АВ в этом случае определяется из соотношения
Модули скоростей точек В и С как вращательные – из соотношений
Расстояния АРАВ, BPАВ и СРАВ определим путем рассмотрения треугольников АВРАВ и АСРАВ, применив теоремы синусов и косинусов. Для заданного положения механизма получим
откуда
Подставив найденные значения расстояний в соответствующие формулы, получим
Вектор Направления скоростей показаны на рис. 10, б. 2. Для определения ускорений точек B, С и углового ускорения звена АВ воспользуемся векторным равенством, выбрав за полюс точку А, ускорение которой известно по величине и направлению:
где Ускорение точки А кривошипа в общем случае складывается из центростремительной
Вектор ускорения точки А направлен к центру вращения звена О (рис. 10, в). Центростремительное ускорение точки В определяется по формуле
Вектор Что касается ускорения точки В – Зададимся произвольно их направлениями по указанным линиям (см. рис. 10, в) и спроектируем уравнение (1) на оси координат. Знак в ответе покажет, соответствует ли истинное направление вектора принятому при расчете. Выбрав направления осей х и у, как показано на рис. 10, в, получаем
Из уравнения (2) находим
Направление ускорения Из уравнения (3) получаем
Знак «минус» показывает, что истинное направление Ускорение Угловое ускорение шатуна АВ с учетом того, что здесь
Вычисляя, находим
Направление ускорения 3. Для определения ускорения точки С воспользуемся векторным уравнением
Вращательное и центростремительное ускорения точки С во вращательном движении звена АВ вокруг полюса А определяются следующим образом:
Вектор Ускорение точки С находим, проектируя уравнение (4) на оси координат (см. рис. 10, в):
Полное ускорение точки С
Пример решения задачи 4 Условие. Произвести расчет цилиндрического стержня переменного поперечного сечения (рис. 2, в) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σс] = [σр] = 210 МПа и модулем Юнга Е = 2,1·105 МПа. На стержень действуют силы F1 = 500 кН; F2 = 900 кН; F3 = 1500 кН; размеры участков: Решение. Составим уравнение равновесия сил на ось у: Σ Fy = 0; Σ Fy = – RАy + F1 – F2 + F3 = 0, откуда RАy = F1 – F2 + F3 = 500 – 900 + 1500 = 1100 кН. Для определения внутренней продольной силы в различных сечениях выделим участки нагружения стержня. Сечения, разделяющие намеченные три участка, проходят через точки приложения сил и перпендикулярны оси их приложения. Разрежем мысленно стержень по сечениям I – I, II – II, III – III. Из условия равновесия стержня ниже сечения I – I получим, что внутренняя продольная сила NI ‑ I = F1 = 500 кН (растяжение). Из условия равновесия стержня ниже сечений II – II и III – III получим NII ‑ II = F1 – F2 = 500 – 900 = – 400 кН; NIII – III = F1 – F2 + F3 = 500 – 900 + 1500 = 1100 кН. Отрицательное значение NII – II свидетельствует о деформации сжатия на этом участке, положительное значение NIII – III – о растяжении. Выбрав масштаб, построим эпюру продольных сил (рис. 2, б). При этом растягивающую силу считаем положительной, а сжимающую – отрицательной. Из условия равнопрочности всех участков стержня определим площади и диаметры поперечных сечений. На участке между сечениями А – А и В – В А1 = N1 / [σр] = 5 · 105 / 210 · 106 = 2,4 · 10–3 м2, откуда диаметр стержня d1 = 0,055 м. На участке между сечениями В – В и С – С А2 = N2 / [σс] = 4 · 105 / 210 · 106 = 1,9 ·10–3 м2, откуда диаметр стержня d2 = 0,049 м. На участке между сечениями С – С и D – D А3= N3 / [σр] = 1,1 · 106 / 210 · 106 = 5,2 · 10–3 м2, откуда диаметр стержня d3= 0,082 м.
Рис. 2 Для вычисления перемещений определим деформации каждого из трех участков. Для этого преобразуем зависимость, выражающую закон Гука: ε = σ/Ε, где ε = Δ Подставив значения ε и σ, получим Δ откуда Δ Деформацию соответствующих участков находим как Δ Δ Δ Перемещение любого сечения стержня равно сумме деформаций участков, расположенных между сечением и опорой. Перемещение сечения D – D δD – D = 0. Перемещение сечения С – С обусловлено деформацией участков, расположенных между D – D и C – C: δС – С = Δ Перемещение сечения В – В обусловлено деформацией двух участков, расположенных между D – D и C – C, а также между С – С и В – В. Тогда δВ – В = Δ Из аналогичных рассуждений определим перемещение сечения А – А: δА – А = Δ В выбранном масштабе откладываем на эпюре (рис. 2, д) значения δС – С, δВ – В и δА – А и соединяем полученные точки прямыми линиями, так как при действии сосредоточенных внешних сил перемещения линейно зависят от абсциссы сечения. В результате получаем эпюру перемещений δ. Задача 5. Тема «Кручение» Условие. К стальному ступенчатому валу, имеющему сплошное цилиндрическое поперечное сечение, приложены четыре крутящих момента (рис. 3). Левый конец вала жестко закреплен в опоре, а правый – свободен. Требуется:
Рис. 3. Схемы валов к задаче 5 1) построить эпюру крутящих моментов Tк по длине вала; 2) при заданном значении допускаемого напряжения на кручение [τк] определить диаметры d1 и d2 вала из расчета на прочность (полученные результаты округлить). Исходные цифровые данные приведены в табл. 2. Таблица 2
Пример решения задачи 5 Условие. Рассмотрим решение задачи № 8 по варианту, соответствующему шифру зачетной книжки 000. По табл. 2 принимаем: схему 10; Т1 = 6,0 кНм; Т2 = 3,0 кНм; Т3 = 2,0 кНм; Т4 = 1,0 кНм; а = 1,9 м; b = 1,9 м; с = 1,9 м; [τ] = 50 МПа. Решение. Для построения эпюры крутящих моментов разобьем вал на участки, границами которых являются характерные сечения (характерные сечения – сечения, в которых приложены внешние крутящие моменты, а также сечения, в которых изменяются поперечные размеры сечения вала). Примем следующее правило знаков для внутреннего крутящего момента. Внутренний крутящий момент в сечении считается положительным, когда внешний момент вращает отсеченную часть вала против часовой стрелки (при взгляде на отсеченную часть со стороны сечения). Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным. Величина крутящего момента в данном сечении равна алгебраической сумме внешних вращающих моментов, приложенных к отсеченной части. Используя метод сечений, определим значения внутренних крутящих моментов на участках вала, разделенных характерными сечениями. I участок: ТкI = Т4 = 1,0 кНм; II участок: ТкII = Т4 – Т3 = 1,0–2,0 = – 1,0 кНм; III участок: ТкIII = Т4 – Т3 + Т2 = 1,0–2,0 + 3,0 = 2,0 кНм; IV участок: ТкIV = Т4 – Т3 + Т2 – Т1 = 1,0–2,0 + 3,0 = 2,0 кНм. Построим эпюру внутренних крутящих моментов Тк (рис. 4). Определим из условия прочности при кручении диаметры вала:
По условию задачи диаметры вала на участках I и II равны. Из анализа эпюры Тк видно, что крутящие моменты, действующие на этих участках, равны по абсолютной величине. Поэтому Тmax = 1 кНм. Тогда
Полученное значение диаметра округляем до ближайшего (в сторону увеличения) из ряда диаметров по ГОСТ 6963–69. Принимаем d1= d2=48 мм. Диаметры вала на участках III и IV по условию задачи одинаковы; Тmax = 4,0 кНм. Тогда, поскольку на четвертом участке действует момент больший, чем на третьем,
Принимаем d1 = 75 мм.
Рис. 4 Пример решения задачи 6 Данная задача относится к теме «Поперечный изгиб». Задачи подобного типа возникают достаточно часто при расчете различных конструкций. Прежде всего необходимо усвоить понятия «поперечная сила (Q)» и «изгибающий момент (M)» и научиться строить эпюры Q и M. Поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения. Изгибающий момент М в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения. Поперечная сила в сечении балки mn (рис. 6, а) считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз, и отрицательной – в противном случае (рис. 6, б).
Рис. 6 Условие. Изгибающий момент М будем считать положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз (рис. 7, а), и отрицательным, если она изгибается выпуклостью вверх (рис. 7, б)
Рис. 7 Решение. Рассмотрим решение задачи № 9 по варианту, соответствующему шифру 000. По табл. 3 принимаем: схему 10; а = 3,8 м; b = 5,0 м; с = 2,7 м; Определим опорные реакции RА и RВ (рис. 8, а): Σ МА ( q·a·a/2 + M – RB·( откуда
Знак «минус» означает, что направление реакции RВ выбрано неверно. Реакция RВ направлена вверх.
Рис. 8 Для определения реакции RA составим уравнение равновесия моментов относительно точки В: Σ МВ ( q·a · (
Проверим правильность определения реакций опор, для чего спроектируем все силы на ось y: Σ Fy ( – q · a + RA – RB – F = – 13 · 3,8 + 59,4 – (–1) – 11 = 0. Определим значения поперечных сил Q изгибающих моментов М на каждом участке балки, применяя метод сечений. I участок: QyI = – q · z. Это уравнение прямой, поэтому достаточно вычислить значение поперечной силы в начале и конце участка, чтобы определить на эпюре Q ее значение в любой точке при 0 < z < a: QyI|z=0 = 0; QyI|z=a = − q · a =− 13 · 3,8 = − 49,4 кН; МxI = − q · z · z/2; МxI|z=0 = 0; МxI|z=a = − q · a ·a / 2 = − 13 ·3,8 · 1,9 = − 93,9 кНм. II участок: QyII = − q · a + RA; QyII|z=a= QyII|z=a+b= − 49,4 + 59,4 = 10 кН; МxII = − q · a · (z − a /2) + RA · (z −a); МxII|z=a = − q · a2 / 2 = − 13 · 3,82 /2 = − 93,9 кНм; МxII|z=a+b = −q · a · (а/2 + b) + RA · b = − 13 · 3,8 · (3,8 / 2 + 5) = = 59,4 · 5 = 43,9 кНм. III участок: QyIII = − q · a + RA; QyIII|z=a+b= QyIII|z= МxIII = − q · a · (z − a /2) + RA · (z −a) − M; МxIII|z=a+b = − q · a · (а/2 + b) + RA · b − M = = − 13 · 3,8 · (3,8 / 2 + 5) =59,4 · 5 − 11= − 54,9 кНм; МxIII|z= = − 13 · 3,8 · (14− 2,7 − 3,8/2) + 59,4· (14 − 2,7 − 3,8) − 11= − 29,7 кНм. IV участок: QуIV = − q∙a + RA – RB = − 49,4 + 59,4 + 1 = 11 кН; МxIV = − q∙a· (z – a/2) + RA (z – a) – M – RB∙ (z – MxIV |z = = − 13 · 3,8 ∙ (14,0 − 2,7 − 3,8/2) + 59,4 (14 − 2,7−3,8) − 11 = − 29,7 кНм; МxIV|z = = − 13 · 3,8 (14 − 3,8/2) + 59,4 (14 – 3,8) − 11 + 1 · 2,7 = 0. Построим эпюру Q (рис. 8, б). Следует обратить внимание на уравнение, согласно которому изменяется Q. На первом участке это уравнение прямой, проходящей через начало координат. При значении z = a Q принимает наибольшее значение. В точке А поперечная сила скачкообразно возрастает на величину RA и затем, как следует из уравнений для QУII и QУIII, остается неизменной до точки В, где скачкообразно возрастает на величину RB. На протяжении IV участка поперечная сила остается постоянной. Аналогичный анализ уравнений изменения изгибающего момента на всех участках следует провести и при построении эпюры М (рис. 8, в). На участке I величина момента изменяется по параболе, причем выпуклость ее направлена вверх. Значения моментов на концах этого участка вычисляются при значениях z, равных соответственно 0 и а. На участках II – IV зависимость момента от координат точки на оси z линейная. В точке приложения сосредоточенного момента на эпюре М возникает скачок, равный его величине. В целом при построении эпюр необходимо обратить внимание на следующую зависимость. На тех участках балки, где изгибающий момент изменяется по параболе (кривая 2-го порядка), поперечная сила изменяется по линейному закону, т. е. эпюра − наклонная прямая (линия первого порядка). Там же, где Ми изменяется по линейному закону (т. е. эпюра Ми – наклонная прямая), а попереч
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1754; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.013 с.) |











 заменим равнодействующей:
заменим равнодействующей: ,
,  ,
,  ; в схеме в:
; в схеме в:  ,
,  ,
,  .
. ,
, .
.
 .
.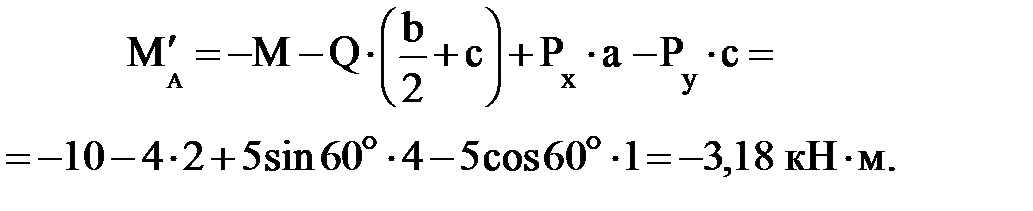
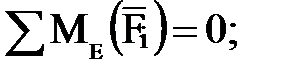
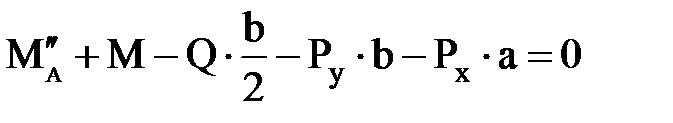 ,
,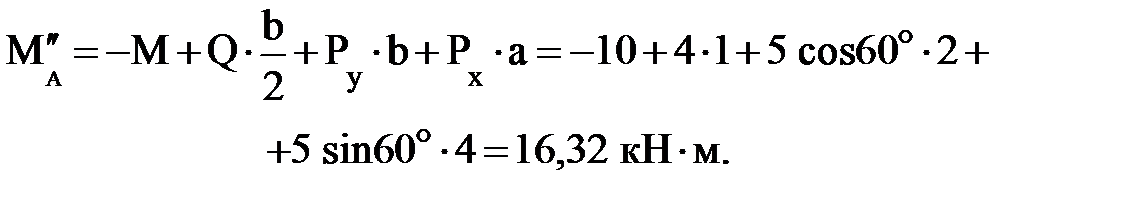

 , откуда
, откуда  кН.
кН.
 , откуда
, откуда  кН.
кН.
 .
. и
и  = 20 см, образующий с горизонтальной плоскостью угол α2=45°. Веревка, намотанная на колесо и натягиваемая грузом F=0,5 кН, сходит с колеса по касательной, наклоненной под углом α1=30° к горизонту. Пренебрегая весом вала, колеса, рычага и трением в блоке, определить вертикальную силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В, если a = 1,8 м, b = 1,0 м, c = 1,6 м (см.рис. 4, схема 10).
= 20 см, образующий с горизонтальной плоскостью угол α2=45°. Веревка, намотанная на колесо и натягиваемая грузом F=0,5 кН, сходит с колеса по касательной, наклоненной под углом α1=30° к горизонту. Пренебрегая весом вала, колеса, рычага и трением в блоке, определить вертикальную силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В, если a = 1,8 м, b = 1,0 м, c = 1,6 м (см.рис. 4, схема 10). (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6)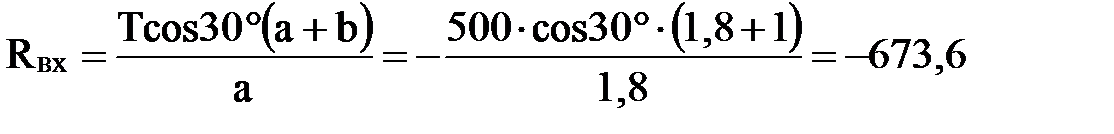 Н.
Н.
 Н.
Н. Н.
Н. Н.
Н.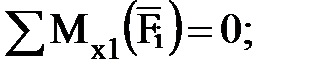
 ;
;
 .
.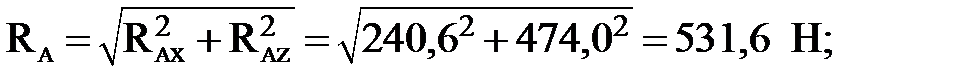

 . Скорость точки А перпендикулярна кривошипу ОА. Для определения скорости точки В найдем положение мгновенного центра скоростейРАВ шатуна АВ, для чего покажем направление скоростей точек А и В (скорость ползуна В имеет вектор по направляющим n – n), а затем из точек А и В восстановим перпендикуляры к скоростям vA и vB. Мгновенный центр скоростей РАВ шатуна АВ находится на пересечении этих перпендикуляров (рис. 10, б).
. Скорость точки А перпендикулярна кривошипу ОА. Для определения скорости точки В найдем положение мгновенного центра скоростейРАВ шатуна АВ, для чего покажем направление скоростей точек А и В (скорость ползуна В имеет вектор по направляющим n – n), а затем из точек А и В восстановим перпендикуляры к скоростям vA и vB. Мгновенный центр скоростей РАВ шатуна АВ находится на пересечении этих перпендикуляров (рис. 10, б). .
. ;
; .
. ,
,


 ;
; ;
; .
. направлен перпендикулярно отрезку СРAB в сторону, соответствующую направлению вращения звена АВ.
направлен перпендикулярно отрезку СРAB в сторону, соответствующую направлению вращения звена АВ. , (1)
, (1) – ускорение ползуна В;
– ускорение ползуна В;  – ускорение точки А, выбранной за полюс;
– ускорение точки А, выбранной за полюс;  – центростремительное (осестремительное, нормальное) ускорение точки В при ее вращении вокруг полюса А;
– центростремительное (осестремительное, нормальное) ускорение точки В при ее вращении вокруг полюса А;  – вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А.
– вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А. и вращательной составляющих
и вращательной составляющих 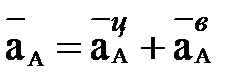 . Поскольку по условию кривошип ОА вращается равномерно, то
. Поскольку по условию кривошип ОА вращается равномерно, то  и ускорение точки А состоит только из центростремительной составляющей, модуль которой определяется по формуле
и ускорение точки А состоит только из центростремительной составляющей, модуль которой определяется по формуле .
. .
. ; (2)
; (2) . (3)
. (3)
 .
. .
. .
.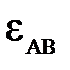 . Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращении звена совпадает с направлением его вращения, а при замедленном – противоположно ему. В данном случае угловое ускорение совпадает с направлением вращения шатуна.
. Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращении звена совпадает с направлением его вращения, а при замедленном – противоположно ему. В данном случае угловое ускорение совпадает с направлением вращения шатуна. ;
; .
. перпендикулярен вектору
перпендикулярен вектору  и направлен соответственно угловому ускорению
и направлен соответственно угловому ускорению  ;
; .
.


 .
. .
. .
.


 i) = 0;
i) = 0; .
.
 .
. −c = − 49,4 + 59,4 = 10 кН;
−c = − 49,4 + 59,4 = 10 кН;


