
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 6. Тема «поперечный изгиб»Содержание книги Поиск на нашем сайте
Условие. Для заданной схемы балки (рис. 5) требуется: 1) записать уравнение в общем виде для определения поперечных сил Q и изгибающих моментов Ми на каждом участке балки; 2) построить эпюры поперечных сил Q и изгибающего момента Mи; 3) найти максимальный изгибающий момент Мmax и подобрать по ГОСТу стальную балку двутаврового поперечного сечения.
Рис. 5. Схемы к задаче 6 Допускаемое напряжение на изгиб принять равным [σи]=150 МПа. Исходные цифровые данные представлены в табл. 3. Таблица 3
Пример решения задачи 6 Данная задача относится к теме «Поперечный изгиб». Задачи подобного типа возникают достаточно часто при расчете различных конструкций. Прежде всего необходимо усвоить понятия «поперечная сила (Q)» и «изгибающий момент (M)» и научиться строить эпюры Q и M. Поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения. Изгибающий момент М в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения. Поперечная сила в сечении балки mn (рис. 6, а) считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз, и отрицательной – в противном случае (рис. 6, б).
Рис. 6 Условие. Изгибающий момент М будем считать положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз (рис. 7, а), и отрицательным, если она изгибается выпуклостью вверх (рис. 7, б)
Рис. 7 Решение. Рассмотрим решение задачи № 9 по варианту, соответствующему шифру 000. По табл. 3 принимаем: схему 10; а = 3,8 м; b = 5,0 м; с = 2,7 м;
Определим опорные реакции RА и RВ (рис. 8, а): Σ МА ( q·a·a/2 + M – RB·( откуда
Знак «минус» означает, что направление реакции RВ выбрано неверно. Реакция RВ направлена вверх.
Рис. 8 Для определения реакции RA составим уравнение равновесия моментов относительно точки В: Σ МВ ( q·a · (
Проверим правильность определения реакций опор, для чего спроектируем все силы на ось y: Σ Fy ( – q · a + RA – RB – F = – 13 · 3,8 + 59,4 – (–1) – 11 = 0. Определим значения поперечных сил Q изгибающих моментов М на каждом участке балки, применяя метод сечений. I участок: QyI = – q · z. Это уравнение прямой, поэтому достаточно вычислить значение поперечной силы в начале и конце участка, чтобы определить на эпюре Q ее значение в любой точке при 0 < z < a: QyI|z=0 = 0; QyI|z=a = − q · a =− 13 · 3,8 = − 49,4 кН; МxI = − q · z · z/2; МxI|z=0 = 0; МxI|z=a = − q · a ·a / 2 = − 13 ·3,8 · 1,9 = − 93,9 кНм. II участок: QyII = − q · a + RA; QyII|z=a= QyII|z=a+b= − 49,4 + 59,4 = 10 кН; МxII = − q · a · (z − a /2) + RA · (z −a); МxII|z=a = − q · a2 / 2 = − 13 · 3,82 /2 = − 93,9 кНм; МxII|z=a+b = −q · a · (а/2 + b) + RA · b = − 13 · 3,8 · (3,8 / 2 + 5) = = 59,4 · 5 = 43,9 кНм. III участок: QyIII = − q · a + RA; QyIII|z=a+b= QyIII|z= МxIII = − q · a · (z − a /2) + RA · (z −a) − M; МxIII|z=a+b = − q · a · (а/2 + b) + RA · b − M = = − 13 · 3,8 · (3,8 / 2 + 5) =59,4 · 5 − 11= − 54,9 кНм; МxIII|z= = − 13 · 3,8 · (14− 2,7 − 3,8/2) + 59,4· (14 − 2,7 − 3,8) − 11= − 29,7 кНм. IV участок: QуIV = − q∙a + RA – RB = − 49,4 + 59,4 + 1 = 11 кН; МxIV = − q∙a· (z – a/2) + RA (z – a) – M – RB∙ (z – MxIV |z = = − 13 · 3,8 ∙ (14,0 − 2,7 − 3,8/2) + 59,4 (14 − 2,7−3,8) − 11 = − 29,7 кНм; МxIV|z = = − 13 · 3,8 (14 − 3,8/2) + 59,4 (14 – 3,8) − 11 + 1 · 2,7 = 0. Построим эпюру Q (рис. 8, б). Следует обратить внимание на уравнение, согласно которому изменяется Q. На первом участке это уравнение прямой, проходящей через начало координат. При значении z = a Q принимает наибольшее значение. В точке А поперечная сила скачкообразно возрастает на величину RA и затем, как следует из уравнений для QУII и QУIII, остается неизменной до точки В, где скачкообразно возрастает на величину RB. На протяжении IV участка поперечная сила остается постоянной.
Аналогичный анализ уравнений изменения изгибающего момента на всех участках следует провести и при построении эпюры М (рис. 8, в). На участке I величина момента изменяется по параболе, причем выпуклость ее направлена вверх. Значения моментов на концах этого участка вычисляются при значениях z, равных соответственно 0 и а. На участках II – IV зависимость момента от координат точки на оси z линейная. В точке приложения сосредоточенного момента на эпюре М возникает скачок, равный его величине. В целом при построении эпюр необходимо обратить внимание на следующую зависимость. На тех участках балки, где изгибающий момент изменяется по параболе (кривая 2-го порядка), поперечная сила изменяется по линейному закону, т. е. эпюра − наклонная прямая (линия первого порядка). Там же, где Ми изменяется по линейному закону (т. е. эпюра Ми – наклонная прямая), а поперечная сила Q постоянна, эпюра – горизонтальная прямая (линия нулевого порядка). Вообще порядок уравнения, описывающего закон изменения Q, на единицу ниже порядка уравнения, выражающего закон изменения Ми. Как следует из эпюры Ми, опасное сечение будет расположено на опоре А, где действует максимальный изгибающий момент Мmax = 93,9 кНм. Из условия прочности при изгибе
определим необходимый момент сопротивления балки:
Согласно ГОСТ 8239 – 72 подбираем двутавр с моментом сопротивления Wx, ближайшим к вычисленному (приложение). Таковым является двутавр № 36, у которого Wx = 743 см3. Вычислим максимальное нормальное напряжение в рассчитываемой балке:
что меньше допускаемого напряжения [σ] = 150 МПа. При расчете консольно закрепленной балки (задача 10) можно использовать вышеизложенную методику решения задачи.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.96.202 (0.009 с.) |











 , м
, м


 i) = 0;
i) = 0; .
.
 .
. −c = − 49,4 + 59,4 = 10 кН;
−c = − 49,4 + 59,4 = 10 кН; σ =
σ = 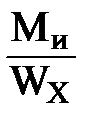 ≤ [σ]
≤ [σ] =
= 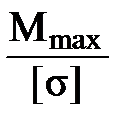 =
= 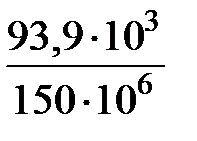 = 0, 626 · 10–3 м3= 626 см3.
= 0, 626 · 10–3 м3= 626 см3. ,
,


