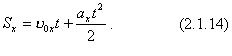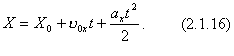Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прискорення – це векторна фізична величина, що дорівнює відношенню зміни швидкості до часу, протягом якого ця зміна відбулася.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Якщо швидкість за будь-які однакові проміжки часу збільшується на ту саму величину, то такий рух називається рівноприскореним. Якщо швидкість тіла зменшується згодом на ту саму величину, то рух називають рівносповільненим. У цілому рівнозмінним називають такий рух тіла, за якого прискорення є сталим ( Прискорення обчислюють як скалярну величину – проекцію вектора прискорення – і формулу (2.1.8) можна записати в скалярній формі:
Проекція вектора прискорення буде мати знак «+», якщо напрям вектора прискорення збігається з напрямом вектора Для побудови графіка прискорення прямолінійного рівнозмінного руху по осі ординат відкладають прискорення, а по осі абцис – час. Оскільки під час рівнозмінного руху прискорення не змінюється, то графік прискорення є прямою, паралельною осі часу. На рис.2.1.16 показано графік прискорення прямолінійного рівноприскореного руху I (а = 2 м/с2) і рівносповільненого II (а = - 4 м/с2).
Із формули (2.1.8) легко визначити миттєву швидкість прямолінійного рівноприскореного руху:
Швидкість рівнозмінного руху є лінійною функцією часу. Із формули (2.1.10) знайдемо значення проекції вектора швидкості на вісь Ох:
Характерні графіки швидкості рівнозмінного руху матеріальної точки для різних випадків показано на рис.2.1.17, на якому: а – графік швидкості рівноприскореного руху без початкової швидкості; б – графік швидкості рівноприскореного руху з початковою швидкістю; в – графік швидкості рівносповільненого руху. В усіх випадках графіки швидкості прямолінійного рівнозмінного руху мають вигляд прямих ліній, проведених під кутом до осі часу. Використовуючи формулу (2.1.10) варто мати на увазі, що напрям однієї з осей системи відліку збігається з напрямом вектора початкової швидкості Середню скалярну швидкість рівнозмінного руху можна знайти як середнє арифметичне початкової v0 і кінцевої vt швидкостей у цьому інтервалі часу:
Якщо відомі час і середня скалярна швидкість, то шлях, пройдений матеріальною точкою за рівнозмінного руху,
Після підстановки значення середньої швидкості (2.1.11) у рівняння (2.1.12) одержуємо
Підставляючи замість
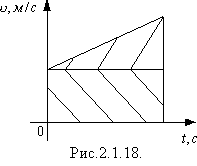
Рівняння (2.1.13) можна одержати іншим способом на підставі графіка швидкості рівноприскореного руху з початковою швидкістю (рис.2.1.18). На цьому графіку пройдений шлях чисельно дорівнює площі трапеції, яку можна подати як суму площ прямокутника і трикутника (на рис.2.1.13 заштриховані). Таким чином, числове значення шляху рівноприскореного руху:
Площа прямокутника дорівнює добутку основи t на висоту v0:
Площа трикутника дорівнює половині добутку основи t на висоту vt –v0:
З огляду на те, що vt –v0 =at, одержують:
Якщо тіло рухається рівноприскорено без початкової швидкості (v0=0), то пройдений шлях:
Таким чином, шлях, пройдений тілом у рівнозмінному русі, є квадратичною функцією часу і завжди додатною величиною. Графіки шляху для різних видів прямолінійного рівнозмінного руху показано на рис.2.1.19: І – рівноприскореного руху з початковою швидкістю; ІІ – рівноприскореного руху без початкової швидкості; ІІІ – рівносповільненого руху. Графіки шляху І і ІІ прямолінійного рівноприскореного руху є гілками парабол, вершини яких знаходяться в початку координат. У першому випадку крива піднімається крутіше, тобто з двох тіл, що рухаються з однаковими прискореннями,
Графік шляху ІІІ рівносповільненого руху показано до моменту часу
Графік цього шляху показано пунктирною лінією (рис.2.1.19). Він подібний до графіка шляху ІІ, але вершина його гілки параболи виходить не із початку осей координат, а з точки, де відбулася зміна напряму руху. Із формули (2.1.13) для проекції переміщення під час рівноприскореного руху знаходимо:
Для знаходження координати X точки в будь-який момент часу t потрібно до початкової координати X 0 додати проекцію вектора переміщення на вісь Ох (рис.2.1.20):
З виразів (2.1.14) і (2.1.15) дістаємо:
Вираз (2.1.16) називають рівнянням рівнозмінного прямолінійного руху (кінематичний закон цього руху). Права частина формули (2.1.16) є алгебраїчною сумою, оскільки X 0, v0x, ax можуть бути додатними і від'ємними. Можливі залежності координати від часу у разі рівнозмінного руху зображено на рис.2.1.21.
Отже, основними рівняннями, що описують прямолінійний рівнозмінний рух точки, є рівняння (2.1.8), (2.1.10), (2.1.13) і (2.1.16). У цих рівняннях у разі рівносповільненого руху прискорення від'ємне. Якщо з формули (2.1.9) визначити значення t і підставити його в (2.1.13), то після перетворень дістанемо рівняння прямолінійного рівнозмінного руху такого вигляду:
Якщо прямолінійний рівноприскорений рух тіла починається зі стану спокою (v0=0), то рівняння (2.1.17) набуває вигляду
або
Формули (2.1.17) – (2.1.19) часто використовують для розв'язання задач.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 ).
).
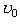 , і знак «-«у випадку протилежного напряму цих векторів. На підставі формули (2.1.9) встановлюють одиниці вимірювання прискорення. Як одиницю прискорення в СI взято прискорення 1 м/с2 – це прискорення такого рівнозмінного руху, під час якого швидкість за 1 с змінюється на 1 м/с.
, і знак «-«у випадку протилежного напряму цих векторів. На підставі формули (2.1.9) встановлюють одиниці вимірювання прискорення. Як одиницю прискорення в СI взято прискорення 1 м/с2 – це прискорення такого рівнозмінного руху, під час якого швидкість за 1 с змінюється на 1 м/с.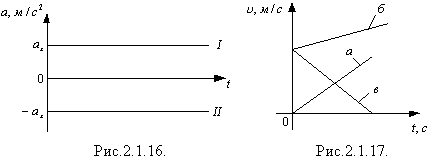


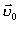 . Якщо вектор прискорення
. Якщо вектор прискорення  спрямовано протилежно вектору
спрямовано протилежно вектору  у деякий момент часу може виявитися від'ємним. Це означає, що швидкість
у деякий момент часу може виявитися від'ємним. Це означає, що швидкість 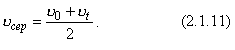


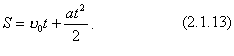
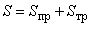
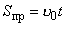 .
. .
. . Додаючи площі S пр і S тр, знаходять вираз для шляху рівнозмінного руху у вигляді рівняння (2.1.13)
. Додаючи площі S пр і S тр, знаходять вираз для шляху рівнозмінного руху у вигляді рівняння (2.1.13)
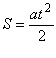
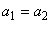 , раніше пройде заданий шлях те тіло, початкова швидкість якого більша. За графіком шляху рівноприскореного руху можна визначити швидкість руху точки.
, раніше пройде заданий шлях те тіло, початкова швидкість якого більша. За графіком шляху рівноприскореного руху можна визначити швидкість руху точки.
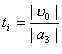 , коли швидкість змінює свій знак на протилежний (за умови, що до зупинки і після неї прискорення за модулем і напрямом залишається сталим). Коли зміниться напрям руху на протилежний початковому, шлях можна обчислити за формулою
, коли швидкість змінює свій знак на протилежний (за умови, що до зупинки і після неї прискорення за модулем і напрямом залишається сталим). Коли зміниться напрям руху на протилежний початковому, шлях можна обчислити за формулою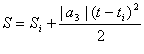 .
.