
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівномірний рух по колу. Період і частота обертання. Лінійна і кутова швидкості. Доцентрове прискорення.Содержание книги
Поиск на нашем сайте
Найпростішим видом криволінійного поступального руху тіла є його рух по колу, коли всі точки цього тіла рухаються по однакових колах. Такий рух зустрічається досить рідко: так рухаються кабінки оглядових коліс у міських парках. Водночас будь-який складний криволінійний рух тіла на досить малій ділянці його траєкторії можна наближено розглядати як рівномірний рух по колу. Тому вивчати довільний криволінійний рух треба починати від простішого: вивчення рівномірного руху по колу. Прикладами рівномірного руху по колу можна наближено вважати: рух штучних супутників Землі, рух частин, що обертаються в механізмах тощо. Почнемо вивчення цього руху з важливої кінематичної величини - миттєвої швидкості. Миттєва швидкість у будь-якій точці криволінійної траєкторії руху тіла напрямлена по дотичній до траєкторії в цій точці. У цьому можна переконатися, спостерігаючи за роботою на точилі. Якщо притиснути до обертового точильного каменя кінець стальної дротини, то розжарені частинки, що відриваються від каменя, буде видно у вигляді іскор. Ці частинки летять з тією швидкістю, яку вони мали в момент відривання від каменя. Напрям руху іскор збігається з дотичною до кола в тій точці, де дротина торкається каменя. По дотичній до кола рухаються також бризки від коліс буксуючого автомобіля. Модуль миттєвої швидкості під час рівномірного руху по колу з плином часу не змінюється. Рівномірним рухом по колу називають рух, під час якого тіло (матеріальна точка) за будь-які рівні проміжки часу проходить однакові відрізки дуг. Прикладами рівномірного руху по колу можна наближено вважати: рух штучних супутників Землі, рух частин, що обертаються в механізмах тощо. Швидкість такого руху матеріальної точки по лінії (колу) за модулем стала і в кожній точці кола напрямлена по дотичній. Положення точки А, що рухається вздовж кола, визначають радіус-вектором
Швидкість руху тіла по колу (лінійну швидкість) за аналогією з рівномірним прямолінійним рухом можна знайти за формулою
де l - довжина дуги кола, пройденої матеріальною точкою за час t. Лінійна швидкість чисельно дорівнює модулю миттєвої швидкості (рис.2.1.23):
Нехай тіло здійснить один оберт по колу, тоді формула (2.1.20) набуде вигляду
де Т - це час одного оберту по колу радіусом R, с. Цей час називають періодом обертання. Лінійну швидкість вимірюють в метрах за секунду (м/с). Набагато частіше в природі й техніці зустрічається обертальний рух тіла, коли нерухомою залишається одна точка або сукупність точок, що лежать на осі обертання. Таким є рух дзиґи, колеса нерухомого велосипеда, стрілок годинника тощо. Під час обертання навколо нерухомої осі О різні точки 1, 2, 3 тіла (рис.2.1.24) матимуть різні лінійні швидкості
Як видно з рис.2.1.24 кожна з точок цього диска має свою лінійну швидкість, бо за один і той же час вони проходять відповідно відрізки дуг l 1> l 2> l 3. Однаковою для цих точок буде кутова швидкість обертання. Кутова швидкість w точки, що рівномірно рухається по колу, чисельно дорівнює відношенню кута j, на який повертається радіус-вектор, до часу t і залишається сталою:
У фізиці кути вимірюють в радіанах (рад). Радіан - це безрозмірна одиниця вимірювання плоского кута. Один радіан відповідає центральному куту, довжина дуги якого точно дорівнює радіусу кола. У градусах радіан становить 57о30'. Центральний кут для кола становить 2
Отже, одиницею вимірювання кутової швидкості є 1 рад/с, що відповідає швидкості точки, яка обертається рівномірно й радіус-вектор якої за 1 с описує кут в 1 рад. А формула (2.1.22) для одного оберту по колу набуде вигляду
де 2p відповідає куту 2p радіан; Т - періоду обертання, с. Величину, обернену до періоду обертання, називають частотою обертання і вимірюють кількістю обертів за одиницю часу ([ n ] = 1/c):
Для довільної кількості обертів частоту обертання знаходять за формулою:
де N - кількість обертів, t - час обертання тіла. Після підстановки виразу для частоти обертання (2.1.24) формула (2.1.21) набуде вигляду Знайдемо співвідношення лінійної і кутової швидкостей на підставі формул (2.1.21) (2.1.23):
Оскільки лінійна швидкість змінюється за напрямом, то матеріальна точка, що рухається по колу, набуває прискорення. Прискорення тіла, яке рівномірно рухається по колу, в будь-якій його точці є доцентровим, тобто напрямлене по радіусу кола до його центра. У будь-якій точці вектор прискорення перпендикулярний до вектора швидкості. Цю особливість прискорення рівномірного руху по колу зображено на рис.2.1.26. Чому дорівнює модуль доцентрового прискорення? Числове значення (модуль) прискорення можна легко знайти з рис.2.1.26.
Трикутник, утворений векторами
де
Оскільки розглядуваний інтервал часу t дуже малий, то
Підставивши у рівняння (2.1.26) вирази (2.1.20), (2.1.23), (2.1.25) для
Таким чином, під час рівномірного руху по колу в усіх точках кола доцентрове прискорення за модулем однакове. Проте напрямлене воно завжди по радіусу до центра (рис.2.1.27) так, що напрям прискорення від точки до точки змінюється. Тому рівномірний рух тіла по колу не можна вважати рівноприскореним. Будь-який рух по криволінійній траєкторії можна подати як рух по дугах кіл різних радіусів. Одну зі складних траєкторій, по якій рухається тіло, і доцентрове прискорення тіла в різних її точках зображено на рис.2.1.28:
Отже, в будь-якій точці криволінійної траєкторії тіло рухається з прискоренням, напрямленим до центра того кола, частиною якого є ділянка траєкторії поблизу цієї точки. А модуль прискорення залежить від швидкості тіла та від радіуса відповідного кола.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.157.241 (0.009 с.) |

 , проведеним з центра кола О до цієї точки (рис.2.1.22). Модуль радіуса-вектора дорівнює радіусу цього кола R.
, проведеним з центра кола О до цієї точки (рис.2.1.22). Модуль радіуса-вектора дорівнює радіусу цього кола R.

 .
.
 ,
,  ,
,  , тому не можна говорити про швидкість тіла. Бажано знайти такі характеристики обертального руху тіла, які були б спільними, однаковими для всіх його точок.
, тому не можна говорити про швидкість тіла. Бажано знайти такі характеристики обертального руху тіла, які були б спільними, однаковими для всіх його точок.

 рад, для півкола -
рад, для півкола - 



 , а формула (2.1.23) -
, а формула (2.1.23) -  .
.

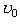 ,
,  і
і  , рівнобедрений, бо
, рівнобедрений, бо  . Трикутник ОАВ на рис.2.1.26 також рівнобедрений, оскільки сторони ОА і ОВ - радіуси кола. Кути при вершинах обох трикутників рівні, бо вони утворені взаємно перпендикулярними сторонами:
. Трикутник ОАВ на рис.2.1.26 також рівнобедрений, оскільки сторони ОА і ОВ - радіуси кола. Кути при вершинах обох трикутників рівні, бо вони утворені взаємно перпендикулярними сторонами:  і
і  . Тому трикутники подібні як рівнобедрені з рівними кутами при вершинах. З подібності трикутників випливає пропорційність відповідних сторін:
. Тому трикутники подібні як рівнобедрені з рівними кутами при вершинах. З подібності трикутників випливає пропорційність відповідних сторін: ,
, . Тому можна записати:
. Тому можна записати:
 - це модуль прискорення. Отже,
- це модуль прискорення. Отже,






