
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Змістовний модуль №2. Похідна функції комплексної змінноїСодержание книги
Поиск на нашем сайте
2.1 Функції із С в С. Границя, неперервність Комплексною функцією комплексної змінної називається функція
Частіше за все ми будемо розглядати функції
1) кожна точка множини 2) будь-які дві точки множини Приклад області:
Однозначна функція комплексної змінної Оскільки кожне комплексне число характеризується парою дійсних чисел, то задання комплексної функції Наприклад, Означення2. Однозначна функція Далі ми будемо вважати, що множина Наприклад, Нехай Означення3 (Коші).
Означення4 (Гейне).
Теорема1. Нехай
Доведення див. [2, с. 60]. З цієї теореми слідує виконання всіх властивостей границі функції аналогічні властивостям границі дійсних функцій. Розглянемо функцію Означення5. Функція Неперервність Всі властивості неперервних функцій аналогічні властивостям неперервних функцій дійсної змінної див. [2, 3]. Якщо функція неперервна в кожній точці області Приклад 1.
Розв’язання.
Тоді Приклад 2. Знайти Розв’язання. Вправи
|
||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 , у якої область визначення
, у якої область визначення  та множина значень
та множина значень  належать множині комплексних чисел
належать множині комплексних чисел  . Ці функції також можна вважати як відображення із
. Ці функції також можна вважати як відображення із 
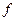 , у яких областю визначення є область.
, у яких областю визначення є область. - окіл
- окіл 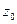 –
–  – відкритий круг радіуса
– відкритий круг радіуса  Означення1. Множина
Означення1. Множина  називається областю, якщо виконуються наступні умови:
називається областю, якщо виконуються наступні умови: – внутрішня (існує
– внутрішня (існує  , всі точки якого належать
, всі точки якого належать 
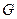 , визначається законом, який ставить кожному
, визначається законом, який ставить кожному  у відповідність одне визначене комплексне число
у відповідність одне визначене комплексне число 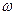 . Символічно це записується
. Символічно це записується 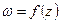 .
. комплексної змінної
комплексної змінної  еквівалентне введенню двох дійсних, тобто
еквівалентне введенню двох дійсних, тобто  ,
,  ,
, 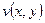 визначені в області
визначені в області  , а
, а  .
.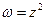 ,
,  , тобто
, тобто  ,
,  .
.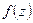 називається однолистковою функцією в області
називається однолистковою функцією в області  – значень функції
– значень функції  ставиться у відповідність одна або декілька
ставиться у відповідність одна або декілька 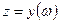 – обернена
– обернена 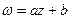 , тоді обернена функція
, тоді обернена функція  однозначна функція.
однозначна функція. називається границею
називається границею  , якщо
, якщо 
 таке, що
таке, що 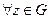 і такого, що
і такого, що  виконується нерівність
виконується нерівність .
. , яка збігається до
, яка збігається до  , послідовність
, послідовність  збігається до
збігається до  .
.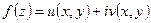 ,
,  гранична точка області визначення
гранична точка області визначення  необхідно і достатньо, щоб виконувались співвідношення
необхідно і достатньо, щоб виконувались співвідношення ,
,  .
. , тоді нескінченно віддалена точка
, тоді нескінченно віддалена точка 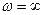 визначається як точка, що відповідає початку координат
визначається як точка, що відповідає початку координат 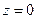 при цьому
при цьому  .
. , якщо
, якщо  .
. .
. .
.

 при
при  ,
,  .
. або
або  і підставляючи в
і підставляючи в  отримаємо
отримаємо  – парабола. Таким чином пряма
– парабола. Таким чином пряма  .
. .
. ,
, 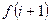 ,
,  –?
2.
–?
2.  .
3.
.
3. 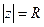 .
4.
.
4.  . Знайти образ
. Знайти образ  . Знайти образ
. Знайти образ  .
6.
.
6.  .
.
 .
8.
.
8.  .
9.
.
9.  .
10.
.
10.  .
.



