
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Змістовний модуль №1. Комплексні числа та їх геометричне представлення 5Стр 1 из 11Следующая ⇒
Зміст Змістовний модуль №1. Комплексні числа та їх геометричне представлення 5 1.1. Комплексні числа. Форми запису комплексного числа. Дії над комплексними числами. 5 1.2. Послідовності і ряди комплексних чисел. Степеневий ряд. 8 Змістовний модуль №2. Похідна функції комплексної змінної 11 2.1 Функції із С в С. Границя, неперервність. 11 2.2. Похідна функції комплексної змінної. Умови диференційованості 14 2.3. Геометричний зміст модуля і аргументи похідної комплексної функції 17 2.4. Означення аналітичної функції. Поняття Конформного відображення. 18 Змістовний модуль №3. Елементарні аналітичні функції 22 3.1. Лінійна функція. 22 3.2. Дробово-лінійна функція. 23 3.3. Степенева функція. Поверхня Рімана. 26 3.4. Функція Жуковского. 28 3.5. Показникова функція комплексної змінної 30 3.6. Тригонометричні функції 31 3.7. Логарифмічна функція. Точка розгалуження. 33 3.8. Радикал. Загальна степенева функція. 35 3.9. Обернені тригонометричні функції 36 Змістовний модуль №4. Інтеграл функції комплексної змінної 37 4.1. Інтеграл від функції комплексної зміної по кусочно-гладкому контуру. 37 4.2. Теорема Коші 39 4.3. Невизначений інтеграл. Формула Ньютона-Лейбница. 40 Змістовний модуль № 5. Інтегральна формула Коші та її наслідки. 42 5.1. Формула Коші. Принцип максимума модуля. 42 5.2. Цілі функції. Теорема Ліувіля. Основна теорема алгебри. 43 5.3. Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду 44 5.4. Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності 45 5.5. Аналітичне продовження. Елементарні функції як аналітичні продовження 46 Змістовний модуль № 6. Ізольовані особливі точки аналітичних функцій 48 6.1. Розкладання аналітичної функції в ряд Лорана. 48 6.2. Класифікація ізольованих особливих точок. Нескінченно віддалена особлива точка. Критерій особливої точки, яка усувається. 49 6.3. Критерій полюса. 50 6.4. Теорема Сохоцького-Вейєрштрасса. 51 6.5. Раціональні і міроморфні функції 52 Змістовний модуль № 7. Лишки та їх застосування. 53 7.1. Означення ЛишкА. Обчислення лишків. 53 7.2. Основна теорема теорії лишків. 54 7.3. Застосування теореми лишків до обчислення визначених інтегралів. 55 Контрольні роботи. 58 Контрольна робота №1 (денна форма навчання) 58
Контрольна робота №2 (денна форма навчання) 72 Контрольна робота (заочна форма навчання) 88 Зразки розв'язування задач. 94 Література. 105
Змістовний модуль №1. Комплексні числа та їх геометричне представлення Приклад 1. Обчислити Розв’язання.
Вправи 1. Виконати дії: 1) 2. Знайти модуль і аргумент та представити в тригонометричній формі: 7) 3. Обчисліть: 12) 4. Визначте геометричний зміст: 16) 19) Вправи Дослідити збіжність рядів. Знайти область збіжності.
Приклад 1.
Розв’язання.
Тоді Приклад 2. Знайти Розв’язання. Вправи
Приклад 2.
Розв’язання
Вправи Показати, що функції диференційовані 1. 2. 3. Довести, що функції не диференційовані. 4. 5. 6. Знайти Знайти аналітичну функцію 7. 8. 9. 10. При якому
Вправи Знайти коефіцієнт розтягнення і кут повороту при заданих відображеннях в заданих точках 1. 2. 3. Яка частина комплексної площини розтягується, а яка стискається (вправи 4, 5, 6). 4. 5. 6. 7.
Вправи Знайти точки, в яких відображення конформне (І-го роду). 1) 2) 3) 4) Чи конформні відображення у нескінченно віддаленій точці 5) 6) 7) 8) Покажіть, що відображення здійснюють конформне відображення ІІ-го роду 9) 10)
Лінійна функція Означення1. Функція виду Функція визначена та однозначна для будь-якого z та оскільки
При цьому відображенні у всіх точках z дотична до довільної кривої, яка проходить через z, повертається на один і той самий кут Якщо a =1, то Якщо a Таким чином Приклад1.
Площина z повертається на кут
Вправи Знайти лінійні відображення: 1. яке відображує трикутник з вершинами 0,1, і на подібний трикутник 0,2, 1+ і. 2. з нерухомою точкою 1+2 і, яке переводе точку і у b-i. 3. яке переводе верхню півплощину на себе. 4. яке переводе верхню півплощину на нижню півплощину. 5. яке переводе верхню півплощину на праву півплощину. 6. яке переводе праву півплощину на себе. 7. яке переводе праву півплощину на ліву. 8. яке переводе смугу 0< x <1 на себе. 9. яке переводе смугу 2< y <1 на себе. 10. яке переводе смугу, яка обмежена прямими y=x, y=x –1 на себе.
Дробово-лінійна функція
Означення2. Функція Для Оскільки З Залишається розглянути – чи конформне відображення Із визначення конформності відображення у нескінченно віддаленій точці, треба розглянути конформність відображення Нехай Таким чином, можна зробити висновок: дробово-лінійна функція Теорема1. Заданням відповідності трьом різним точкам розширеної площини z трьох різних точок розширеної площини Тобто, якщо
Теорема2 (колова властивість). Дробово-лінійна функція переводе кола та прямі на площині z у кола та прямі на площині Доведення теореми див. [1, с. 162-163].
Приклад1. Знайти функцію, яка конформно відображає коло Розв’язання.
Встановимо відповідність: (границя повинна переходити в границю) та повинно зберігатися направлення обходу області тоді, оскільки
Знайдемо Вправи У що відображаються наступні області? 1. квадрат 2.півколо Знайти дробово-лінійне відображення, яке переводе точки – 1,i,i+1 у точки 3. 0, 2i, 1– i; 4. i, Знайти дробово-лінійне відображення, яке переводе точки - 1, 5. i, 1, 1+i; 6. Знайти загальний вид дробово-лінійного відображення, яке переводе: 7. верхню півплощину на себе; 8. верхню півплощину на нижню; 9. верхню півплощину на одиничне коло; 10. верхню півплощину на праву півплощину.
Вправи 1) відобразити кут 2) кут 3) кут 4) кут 5) кут 6) кут Знайти образ областей при відображенні: 7) 8) 9) 10)
Функція Жуковского
Означення4. Функція виду Якщо довизначити Теорема4. Функція Теорема5. Функція Доведення теореми див.[2, 130-133]. Візьмемо дві площини Приклад1. Відобразити півколо Розв’язання: Вправи Знайти область, у які функція Жуковського відображає: 1) 2) 3) 4) 5) Відобразити вказані області на верхню півплощину: 6) 7) 8) 9) 10)
Властивості 1) 2) 3) Теорема6. Показникова функція
Наслідок. Смуга Доведення див. [3, с. 91]. Поверхня Рімана, у яку конформно відображається розширена площина z будується наступним чином: потрібно взяти нескінченно багато площин Приклад1. Відобразити Розв’язання: Вправи Вияснити, у що перетворюється за допомогою 1) пряма 2) смуга 3) півсмуга 4) півсмуга 5) прямокутник Знайти відображення, яке переводе: 6) смугу 7) смугу 8) смугу 9) смугу 10)
Тригонометричні функції
Означення6. Функції Властивості: 1) 2) 3) 4) всі тригонометричні формули виконуються для 5) Оскільки, Теорема7. Функція Доведення тереми див. [2, с.160]. Поверхня Римана Приклад1. З’ясувати, у що перетворюється пряма Розв’язання:
Тоді u= або
Тобто Вправи З’ясувати, у що перетворюється при відображенні 1) 2) 3) смуга 4) півсмуга 5) прямокутник 6) півсмуга 7) півсмуга 8) півсмуга 9) смуга 10) півсмуга
Вправи Знайти значення: 1) 2) 3) 4) 5) У що перетворюються при відображенні 6) 7) 8) 9) сектор 10) спіраль
Вправи Обчислити: 1)
| Поделиться:
| |
 .
. ,
,  ,
, .
.
 ,
,  .
. ,
, 
 ,
, 
 ,
, 

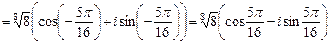 ,
,  .
. ; 2)
; 2) 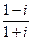 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  .
. ; 8)
; 8) 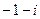 ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11)  .
.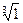 ; 13)
; 13)  ; 14)
; 14)  ; 15)
; 15)  .
. ; 17)
; 17)  ; 18)
; 18)  ;
; ; 20)
; 20) 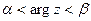 .
.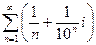 2.
2.  3.
3.  4.
4.  5.
5. 
 7.
7.  8.
8.  9.
9. 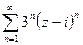 10.
10. 
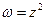 . Знайти образ лінії
. Знайти образ лінії  .
.
 ;
; 
 при
при  ,
,  .
. або
або  і підставляючи в
і підставляючи в  отримаємо
отримаємо  – парабола. Таким чином пряма
– парабола. Таким чином пряма  .
. .
. ,
, 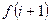 ,
,  –?
2.
–?
2.  .
3.
.
3.  . Знайти образ
. Знайти образ 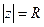 .
4.
.
4.  . Знайти образ
. Знайти образ  . Знайти образ
. Знайти образ  .
6.
.
6.  .
.
 .
8.
.
8.  .
9.
.
9.  .
10.
.
10.  .
.
 . Знайти
. Знайти 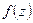 , якщо вона диференційована.
, якщо вона диференційована.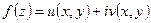 ,
, 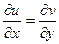 ,
, 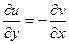 . Оскільки
. Оскільки 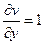 ,
, 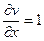 , то
, то 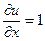 ,
, 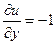 . З останніх рівностей отримаємо, що
. З останніх рівностей отримаємо, що ,
, 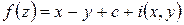 .
.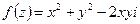 .
. ,
, 
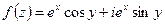 ,
, 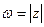 .
.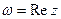 .
.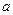 ,
, 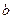 ,
, 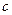 , при яких
, при яких 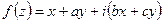 буде аналітичною.
буде аналітичною.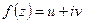 .
.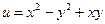 ,
, 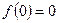 .
.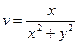 ,
, 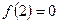 .
. .
.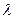
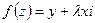 – аналітична?
– аналітична?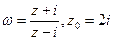 ;
;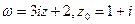 ;
;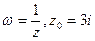 . Знайти
. Знайти  , в яких коефіцієнт розтягнення дорівнює 1.
, в яких коефіцієнт розтягнення дорівнює 1.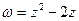 ;
; . Знайти
. Знайти  , в яких кут повороту дорівнює нулю.
, в яких кут повороту дорівнює нулю. ;
;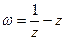 ;
; ;
; .
.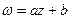 ;
;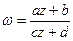 .
. ;
; ,
,  задовольняє теоремі.
задовольняє теоремі.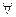 z
z  , то вона здійснює конформне відображення площини z на площину
, то вона здійснює конформне відображення площини z на площину 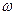 .
.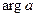 і розтягує площину z у всіх точках на
і розтягує площину z у всіх точках на  .
. ,
,  і розтягування та поворот відсутні, тобто функція
і розтягування та поворот відсутні, тобто функція  зміщує площину
зміщує площину  на вектор
на вектор  1, то
1, то  можна представити
можна представити  , де
, де  , тобто кожен вектор
, тобто кожен вектор  (який виходить з
(який виходить з 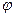 ) повертаючись на
) повертаючись на  .
. ), повертає площину z на кут
), повертає площину z на кут  .
.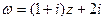 .
. ,
,  .
. та розтягується у
та розтягується у  разів відносно точки –2.
разів відносно точки –2.
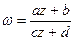 (c≠0) називається дробово-лінійною.
(c≠0) називається дробово-лінійною. дробово-лінійна функція має похідну
дробово-лінійна функція має похідну  та якщо
та якщо  (випадок, коли
(випадок, коли  нецікавий, бо тоді
нецікавий, бо тоді  ), то при
), то при 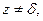
 та відображення
та відображення  здійснює конформне відображення усіх z (
здійснює конформне відображення усіх z ( ).
).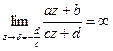 ,
,  , то довизначивши
, то довизначивши  , отримаємо, що
, отримаємо, що  знаходимо, що
знаходимо, що  – обернена функція до
– обернена функція до  , тобто обернена функція до
, тобто обернена функція до  )на розширену площину
)на розширену площину  ?
? у точці z =0,
у точці z =0, 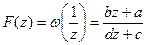 та
та  існує, тобто
існує, тобто  – конформне відображення у z =0, значить
– конформне відображення у z =0, значить  здійснює конформне відображення.
здійснює конформне відображення. . Розглянемо функцію
. Розглянемо функцію  , обернену до вихідної
, обернену до вихідної  зберігає кути та постійність розтягувань при відображенні у
зберігає кути та постійність розтягувань при відображенні у  , але тоді і в обернену сторону відображення
, але тоді і в обернену сторону відображення 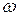 дробово-лінійна функція визначена однозначно.
дробово-лінійна функція визначена однозначно.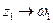 ,
,  ,
,  , то
, то  має вид
має вид :
: 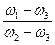 =
=  :
:  .
. на верхню півплощину
на верхню півплощину  .
.



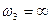 дробово-лінійна функція буде мати вид
дробово-лінійна функція буде мати вид  =
=  .
. Відмітимо, що
Відмітимо, що  , тобто
, тобто  ;
;
 .
.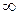 ,1.
,1.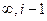
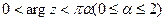 на верхню півплощину;
на верхню півплощину; на праву півплощину;
на праву півплощину; на нижню півплощину;
на нижню півплощину; на ліву півплощину;
на ліву півплощину;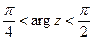 на коло
на коло  на коло
на коло  ,
,  ;
; ;
; ;
;
 називається функцією Жуковського та відображає площину z на площину
називається функцією Жуковського та відображає площину z на площину 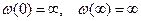 , то отримаємо відображення розширеної площини z на розширену площину
, то отримаємо відображення розширеної площини z на розширену площину 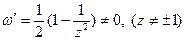 , то
, то  .
.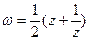 виконує конформне відображення середини одиничного кола на зовнішність відрізку [-1;1] площини
виконує конформне відображення середини одиничного кола на зовнішність відрізку [-1;1] площини 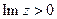 відображається на нижню півплощину
відображається на нижню півплощину 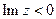 на верхню півплощину
на верхню півплощину  на зовнішність[-1;1] площини
на зовнішність[-1;1] площини  з розрізами по відрізку [-1;1] та „склеїмо” нижній берег розриву
з розрізами по відрізку [-1;1] та „склеїмо” нижній берег розриву  з верхнім берегом розрізу
з верхнім берегом розрізу  , а верхній берег розрізу
, а верхній берег розрізу 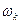 . Отримана дволиста поверхня - поверхня Римана для функції Жуковського, на яку вона конформно відображає розширену площину z.
. Отримана дволиста поверхня - поверхня Римана для функції Жуковського, на яку вона конформно відображає розширену площину z.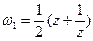 відображає півколо
відображає півколо  . Тому відображення
. Тому відображення 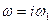 буде шуканим, тобто відображати півколо на праву півплощину.
буде шуканим, тобто відображати півколо на праву півплощину.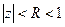 ;
; ;
; .
. ;1];
;1]; ;
; ]
]  ;
; .
. ;
;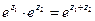 ;
;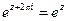 , тобто
, тобто  – період показникової функції.
– період показникової функції. взаємно-однозначно та конформно відображає смугу шириною
взаємно-однозначно та конформно відображає смугу шириною  , паралельну дійсної осі, на кут розчину
, паралельну дійсної осі, на кут розчину  з вершиною в початку координат.
з вершиною в початку координат. конформно відображається на площину
конформно відображається на площину  переходе у верхній берег розрізу, а
переходе у верхній берег розрізу, а 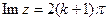 – в нижній берег розрізу.
– в нижній берег розрізу.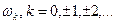 , у яких відтворений розріз по додатній частині дійсної осі. Розміщуючи площини одна під іншою та нижній берег розрізу
, у яких відтворений розріз по додатній частині дійсної осі. Розміщуючи площини одна під іншою та нижній берег розрізу 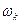 склеїмо з верхнім берегом розрізу
склеїмо з верхнім берегом розрізу  і т. д. Та склеїмо площини у нескінченно віддаленій точці. Отримана нескінченно-листа поверхня – поверхня Римана.
і т. д. Та склеїмо площини у нескінченно віддаленій точці. Отримана нескінченно-листа поверхня – поверхня Римана. за допомогою функції
за допомогою функції  (
(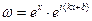 , тобто
, тобто  ,
,  . Тоді
. Тоді  та
та 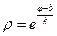 – спіраль.
– спіраль. ;
; ;
; ;
;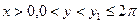 ;
; ;
; 
 на площину;
на площину; у праву півплощину;
у праву півплощину; у ліву півплощину;
у ліву півплощину;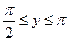 у площину;
у площину;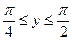 смугу у нижню півплощину.
смугу у нижню півплощину. ,
, 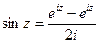 , які визначені на площині z, називаються косинусом та синусом від комплексного z.
, які визначені на площині z, називаються косинусом та синусом від комплексного z.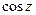 – парна,
– парна, 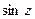 - непарна функції;
- непарна функції; ,
, 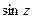 періодичні з періодом
періодичні з періодом  ;
;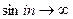
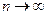 ;
; .
. то достатньо розглянути функцію
то достатньо розглянути функцію 
 конформно відображує на площину
конформно відображує на площину 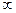 ;-1] та [1;
;-1] та [1;  відображається у нижню півплощину
відображається у нижню півплощину  ,
,  (
(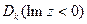 відображається у верхню півплощину
відображається у верхню півплощину 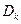 відображається у нижню півплощину
відображається у нижню півплощину  відображається на верхній берег розрізів відповідно[–
відображається на верхній берег розрізів відповідно[–  , в кожній з яких проведено розріз по променям [1;
, в кожній з яких проведено розріз по променям [1;  функцією
функцією 

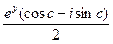

 .
.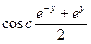 ,
, 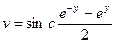
 ,
, 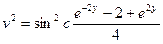 .
. .
.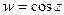 відображає пряму
відображає пряму  у гіперболу
у гіперболу 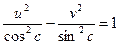 .
.

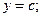
 ;
; ;
;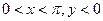 ;
; ;
;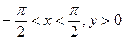 ;
; ;
; .
. ;
; ;
; ;
; ;
; )
)
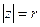 ;
; ;
;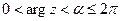 ;
; .
.


