
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цілі функції. Теорема Ліувіля. Основна теорема алгебри
Означення1. Аналітична на всій комплексній площині функція називається цілою функцією. Теорема4 (Ліувіля). Нехай Доведення [3, с.173], [2, с.225]. Приклад1. Застосування теореми Ліувіля є основною теоремою алгебри: Всякий многочлен Доведення слідує з того, що якщо нулів немає, то функція має обмежений модуль і є цілою, не буде константою. Це протиречить теоремі Ліувіля. Отже, припущення щодо відсутності нуля – невірне.
Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду
Теорема5. Функція
Коефіцієнти Доведення теореми див. [2, с.225], [1,с.64]. Нехай
які носять назву нерівність Коші. Приклад1. Розкласти в ряд Розв’язання.
Вправи Розкласти в ряд Тейлора в
Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності
Означення2. Нехай Нехай Якщо Теорема6. Нехай Доведення теореми див. [2. с.263], [1, с.72]. Наслідок 1. Нулі аналітичних функцій – ізольовані точки. Наслідок 2. Нехай Наслідок з теореми являє собою теорему єдиності: Теорема7. Нехай
З теореми єдиності легко отримати: Наслідок 1: Якщо Наслідок 2: Якщо Приклад1. Визначити нулі та їх порядок Розв’язання. Нулями є точки Вправи Знайти порядок нуля z=0 для функцій:
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.63.90 (0.008 с.) |
 – ціла функція, а її модуль обмежений, тоді ця функція – константа.
– ціла функція, а її модуль обмежений, тоді ця функція – константа. - ціла функція і
- ціла функція і  , отже
, отже  - необмежений, тобто існує z такий, що
- необмежений, тобто існує z такий, що 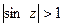 .
. має хоча б один нуль.
має хоча б один нуль.
 розкладається в цьому колі в степеневий ряд:
розкладається в цьому колі в степеневий ряд: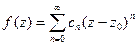 .
.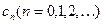 визначаються по формулі
визначаються по формулі  або
або  , де l - будь-який кусочно-гладкий замкнений контур, який повністю належить колу та знаходиться навколо точки
, де l - будь-який кусочно-гладкий замкнений контур, який повністю належить колу та знаходиться навколо точки 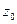 . Ряд визначений однозначно.
. Ряд визначений однозначно. - будь-яка окружність з центром в точці
- будь-яка окружність з центром в точці  , і через
, і через  - максимум модуля
- максимум модуля  ,
, для
для  .
.








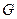 . Точка
. Точка  називається нулем
називається нулем  .
. – нуль
– нуль  . Якщо
. Якщо  ,
,  , де
, де  - аналітична функція в околі
- аналітична функція в околі  і обертається в нуль в різноманітних точках
і обертається в нуль в різноманітних точках 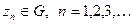 . Якщо послідовність
. Якщо послідовність 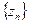 сходиться до
сходиться до  ,
,  в області
в області  функція
функція  , в яких
, в яких  і
і 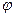 співпадають, то
співпадають, то 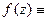
 в
в  ,
,  аналітичні в
аналітичні в  , відповідно і
, відповідно і  , область така, що
, область така, що  , то існує єдина аналітична функція
, то існує єдина аналітична функція 
 .
. . Покажемо, що нулі мають порядок 1. Дійсно,
. Покажемо, що нулі мають порядок 1. Дійсно,  для нуля
для нуля 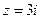 ,
,  та
та  , тобто 3і – нуль першого порядку. Аналогічно для
, тобто 3і – нуль першого порядку. Аналогічно для 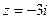 .
.





