
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость линейных сар. Признаки устойчивости. Запасы устойчивости линейных сар.Стр 1 из 6Следующая ⇒
Идентификация статических объектов. Планирование эксперимента. Полный факторный эксперимент.
Планирование эксперимента Большинство научных исследований связано с экспериментом. Он проводится в лабораториях, на производстве, на опытных полях и т.д. Эксперимент может быть физическим, психологическим или модельным. Он может проводиться как на самом объекте так и на модели. Модель, как известно, может отличаться от реального объекта масштабом, а иногда природой (пример). Так что же такое эксперимент? Под экспериментом будем понимать совокупность действий, к которым приходится обращаться, чтобы задавать объекту управления интересующие нас вопросы. Эта совокупность может быть очень сложной, но её всегда можно разложить на отдельные элементы, каждый из которых называется опытом. Существуют и другие определения эксперимента. Одним из возможных путей повышения эффективности исследований является применение математических методов - построение математической теории планирования эксперимента. Планирование эксперимента - это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленных задач с требуемой точностью. При этом существенно следующее: 1) стремление к минимизации общего числа опытов; 2) одновременное варьирование всеми переменными, определяющими процесс, по специальным правилам - алгоритмам; 3) использование математического аппарата, формализующего многие действия эксперимента; 4) выбор чёткой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов. Задачи, для решения которых может использоваться планирование эксперимента (ПЭ), чрезвычайно разнообразны: 1) поиск оптимальных условий; 2) построение интерполяционных формул; выбор существенных факторов; 3) уточнение констант теоретических моделей. Задачи поиска оптимальных условий являются одними из наиболее распространенных научно-технических задач. Они возникают в тот момент, когда установлена возможность проведения процесса и необходимо найти наилучшие условия его реализации. Задачи, сформулированные таким образом, называются задачами оптимизации. Процесс их решения называется процессом оптимизации или просто оптимизацией. Выбор оптимального состава многокомпонентных смесей или сплавов, повышение производительности действующих установок, повышение качества продукции, снижение затрат на её получение - все это примеры задач оптимизации. Эксперимент, который ставится для решения задачи оптимизации - называется экстремальным.
Примеры. Для описания объекта исследования удобно воспользоваться понятием «черного ящика»:
  X1 Y1 X1 Y1
Рис.1 Каждый из факторов может принимать в опыте одно из нескольких значений. Такие значения будем называть уровнями. Каждый фактор имеет определенное число дискретных уравнений. Фиксированный набор уровней факторов определяет одно из возможных состояний черного ящика. Если перебрать все возможные выборы состояний, то получим полное множество различных состояний данного ящика (объекта исследований). Одновременно это будет число возможных различных опытов. Чтобы узнать число различных состояний, достаточно число уровней факторов возвести в степень числа факторов Планирование эксперимента предполагает активное вмешательство в процесс и возможность выбора в каждом опыте тех уровней факторов, которые представляют интерес. Поэтому такой эксперимент называется активным. Объект, на котором возможен активный эксперимент, называется управляемым. На практике нет абсолютно управляемых объектов. На реальный объект обычно действуют как управляемые, так и неуправляемые факторы. Неуправляемые факторы влияют на воспроизводимость эксперимента и являются причиной её нарушения. Если требования воспроизводимости не выполняются, приходится обращаться к активно-пассивному эксперименту. Планирование эксперимента - это метод выбора количества и условий проведения опытов, минимально необходимых для отыскания оптимальных условий, т.е. для решения поставленной задачи. Результаты эксперимента используются для получения математической модели объекта исследований, которая представляет собой уравнение, связывающее, например, оптимизации и факторы. Такое уравнение называют функцией отклика.
Параметр оптимизации При планировании экстремального эксперимента очень важно определить параметр, который нужно оптимизировать. Сделать это совсем не просто, как кажется на первый взгляд. Цель исследования должна быть сформулирована очень четко и допускать количественную оценку. В зависимости от объекта и цели исследования параметры оптимизации могут быть очень разнообразными. Введем некоторую классификацию параметров оптимизации рис.2. Параметр оптимизации - это признак, по которому оптимизируется процесс. Он должен быть количественным, задаваться числом. Его необходимо уметь измерять при любой возможной комбинации выбранных уровней факторов. Множество значений, которые может принимать П.О., будем называть областью его определения. Области определения могут быть непрерывными и дискретными, ограниченными и неограниченными. Например, выход реакции - это параметр оптимизации с непрерывной ограниченной областью определения. Он может изменяться в интервале от 0 до 100%. Число бракованных изделий, число зерен на шлифе сплава, число кровяных телец в пробе крови - это примеры параметров с дискретной областью определения, ограниченной снизу. Рис.2 Классификация параметров оптимизации Уметь измерять параметр оптимизации - это значит располагать подходящим прибором. В некоторых случаях такого прибора может не существовать либо он слишком дорог. Если нет способа количественного измерения результата, то приходится воспользоваться приемом, называем ранжированием (ранговым подходом). При этом П.О. присваиваются оценки - ранги по заранее выбранной шкале: 2х бальной, 5й бальной и т.д. ранговый П.О. имеет дискретную ограниченную область определения. Ранг - это количественная оценка П.о., но она носит условный (субъективный) характер. П.О. должен быть: 1) эффективным с точки зрения достижения цели; 2) универсальным; 3) количественным и выражаться одним числом; 4) статически эффективным (точные измерения); 5) имеющим физический смысл, простым и легко вычисляемым; 6) однозначным. Факторы После того как выбран объект исследования и П.О., нужно включить в рассмотрение все существующие факторы, которые влияют на процесс. Если какой-либо существующий фактор не учтен, то это может привести к неприятным последствиям. Чем больше факторов, то тем больше опытов необходимо провести, так как Выводы: 1. Факторы - это величины, соответствующие способам воздействия внешней среды на объект. Они определяют как сам объект, так и его состояние. Требования к факторам: управляемость и однозначность. Управлять фактором - это значит установить нужное значение и поддерживать его постоянно в течение опыта или менять по заданной программе. В этом состоит особенность активного эксперимента. 2. Планировать эксперимент можно только в том случае, если уровни факторов подчиняются воле экспериментатора. 3. Факторы должны непосредственно воздействовать на объект исследования. Трудно управлять фактором, если он является функцией других переменных, но в планировании эксперимента могут участвовать сложные факторы, такие, как логарифмы, соотношения и т.д. Факторы должны быть определены операционально.
4. Требования к совокупности факторов: совместимость и отсутствие 5. Точность фиксации Ф. должна быть высокая, степень точности определяется диапазоном изменения факторов. Выбор модели Модели бывают разные, ихбывает много. Чтобы выбрать одну из нихнадо понять, что мы хотим от модели, какие требования к ней предъявляем. Главное требование к модели - это способность предсказывать направление дальнейших опытов, причем предсказывать с требуемой точностью. Желательно, чтобы точность предсказания во всех возможных направлениях была одинакова. Это значит, что в некоторой подобласти, в которую входят и координаты выполненных опытов, предсказанные с помощью модели значения функции отклика не должно отличаться от фактического больше чем их некоторую заранее заданную величину. Модель, которая удовлетворяет такому или какому-либо аналогичному требованию, называется адекватной. Разработаны специальные статистические методы проверки адекватности модели. При выборе математической модели, при прочих равных условиях, будем предполагать степенные ряды, т.е. отрезки степенных рядов - алгебраические полиномы. В качестве примера запишем модель в форме полинома для 2х факторов. Полином нулевой степени: Полином первой степени: Полином второй степени: Выбор основного уровня
В разных случаях мы располагаем различными сведениями об области наилучших условий. Если имеются сведения о координатах одной наилучшей точки и нет информации о границах определения факторов, то остается рассматривать эту точку в качестве основного уровня. Аналогичное решение принимается, если границы известны и наилучшие условия лежат внутри области. На рис.2. Изображена область определения для 2х факторов. Кружком отмечены наилучшие условия, известные из априорной информации. Чтобы правильно выбрать основной уровень следует пользоваться блок-схемой рис. 4.
Ошибки параллельных опытов Каждый эксперимент содержит элемент неопределенности вследствие ограниченности экспериментальных данных. Постановка повторных (параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и следует оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в одинаковых условиях несколько раз и затем берется среднее арифметическое всех результатов. Среднее арифметическое Y равно сумме всех m отдельных результатов, делённой на количество параллельных опытов m Отклонение результата любого опыта от среднего арифметического можно представить как разность
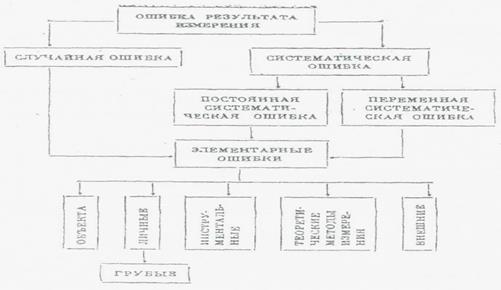
Как правило, ошибка опыта является суммарной величиной, результатом многих ошибок: ошибок измерения факторов, параметра оптимизации и т.д. Все ошибки принято разделять на 2 класса: систематические и случайные.
Рис.8 Схематичное изображение компонент ошибки измерений Для выявления грубых ошибок используют критерий Стьюдента: Значение t берут из таблицы t-распределения Стьюдента. Опыт считается бракованным, если экспериментальное значение t по модулю больше табличного значения. Рандомизация опытов Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (колебанием t°, партий сырья, лаборанта и т.д.), рекомендуется случайная последовательность проведения опытов. Random - случайный. Опыты необходимо рандомизировать во времени. Регрессионный анализ Как только мы начинаем говорить о пригодности модели или о значимости коэффициентов, приходится вспоминать о статистике: и с этого момента МНК превращается в регрессионный анализ.
Регрессионный анализ, как всякий статистический метод, применим при определенных предположениях, постулатах. Первый постулат Параметр оптимизации 7 есть случайная величина с нормальным законом распределения. Дисперсия воспроизводимости - одна из характеристик этого закона распределения. Второй постулат Дисперсия Y не зависит от абсолютной величины Y. Третий постулат Значения факторов суть не случайные величины. Это утверждение практически означает, что установление каждого фактора на заданный уровень и его поддержание существенно точнее, чем ошибка воспроизводимости. Устойчивость линейных САР. Признаки устойчивости. Запасы устойчивости линейных САР. На любую систему автоматического регулирования всегда действуют различные внутренние и внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная САР должна устойчиво работать при всех возмущениях. Определение устойчивости: под устойчивостью понимают способность системы возвращаться с определенной точностью к состоянию равновесия после устранения причин, выведенных систему из состояния равновесия. Для пояснения смысла, понятия устойчивости положения равновесия системы, удобно воспользоваться следующим примером. Пусть имеется некоторая чаша, поставленная дном вниз (рис. 1).
а) Устойчивая система б) Неустойчивая система в) Граница устойчивости На дне чаши (а) в положении равновесия 1 находится тяжелый шарик, который приложенный внешней силой может быть отклонен в положение 2. В определенный момент времени, принимаемый за нулевой, внешняя сила убирается. Шарик, предоставленный сам себе, из положения 2 устремится вниз, и по инерции проскочит положение 1. Затем, достигнув наивысшего положения, уже справа от точки 1, шарик снова будет двигаться вниз. Совершив несколько колебательных движений, шарик из-за наличия сил сопротивления остановится с некоторой точностью в положении равновесия 1, т.е. согласно определению имеет место устойчивость положения равновесия для кратности обозначаемая литерой У. В случае, когда чаша поставлена дном вверх (б). Шарик снова находится в положении равновесия 1 и если к нему не прикладывать никаких сил, то в этом положении он будет находиться сколь угодно долго. Если же некоторой внешней силой переместить шарик в положение 2, а затем убрать эту силу, то шарик удалится от положения 1 на бесконечно большое расстояние и никогда в него не вернется. Такое положение равновесия называется и обозначается В третьем случае (в) изображено нейтральное положение равновесия или граница устойчивости. Если шарик, находящийся на горизонтальной поверхности в положении 1, с помощью внешней силы переместить в положение 2, а затем убрать эту силу, то шарик останется положении 2 до тех пор, пока к нему не будет приложена новая внешняя сила. Случай нейтрального положения равновесия, можно обнаружить и на рис. 1 а, если там не существует сил сопротивления. В этом случае шарик будет совершать незатухающие колебания вокруг положения равновесия 1. Принцип устойчивости САР Обратимся теперь к математической стороне вопроса. Любая система автоматического регулирования с входным сигналом (внешней силой) х и выходным сигналом z, имеющая передаточную функцию: может быть описана линейным неоднородным дифференциальным уравнением Решение этого неоднородного уравнения z(t,)состоит из общего решения zсв(t)-свободная составляющая однородного дифференциального уравнения Из определения устойчивости, данного выше, следует, что устойчивость САР устанавливают в ней, после того как устраняется внешняя сила, выведшая САР из состояния равновесия. Иными словами, устойчивость системы определяет переходный процесс zсв(t), т.е. решение однородного дифференциального уравнения. Таким образом, признаками устойчивости системы являются: если если если Дифференциальному уравнению (3) соответствует характеристическое уравнение корни, которых могут быть либо вещественными (в том числе нулевыми) либо комплексно-сопряженными (в том числе чисто мнимыми). Решение дифференциального уравнения (3) как известно, имеет следующий вид где А, - постоянные интегрирования, определяемые параметрами системы и начальными условиями; рi - корни характеристического уравнения (4.).
Рассмотрим случаи, когда рi –вещественные корни а) пусть рi = аi , где аi >0 корни положительные вещественные
б) пусть pi = -ai, где ai>0 корни отрицательные вещественные
в) пусть есть два комплексно сопряженных корня pi, i+1 = ai ± jβi, где ai >0
г) pi, i+1 =- ai ± jβi, где ai >0
- устойчивая
д) корни мнимые – не содержат действительной части ai = 0. pi,i+1 = ±βit (ai=0) zcв i, i+1(t)= Ai sin βit граница устойчивости -
e) pi = 0 zсв I (t)= Ai - граница устойчивости
Рассмотрим все случаи на плоскости P1 - сл. (а); Р2 – сл. (б); Рк = 0 – сл. (е); Ре, у+1 – сл. (д)
Если все корни характеристического уравнения левые (либо отрицательные, либо имеют отрицательную вещественную часть), то система устойчива. Если среди корней характеристического уравнения хотя бы один – правый, система - неустойчива. Система находится на границе устойчивости, если кроме левых корней есть еще корни, расположенные на мнимой оси. Расположение корней зависит от коэффициентов характеристического уравнения, а следовательно, от параметров системы. a0pn + … + an = 0. Если К2 > К1 – корни сдвинутся вправо. Если К3> К2 – может привести к неустойчивости системы. При переходе корня навстречу штриховке устойчивость уменьшается. Чем больше коэффициент усиления, тем меньше устойчивость (в большинстве случаев). Система, у которой изменением параметра можно изменить устойчивость системы называется структурно-устойчивой системой; в противном случае, когда никакими изменениями параметров неустойчивую систему нельзя сделать устойчивой, называется структурно-неустойчивой системой. Но корни характеристического уравнения можно вычислить только до 4 степени и вычисление их очень трудоемко. Стодола – высказал условие, которое оказалось необходимым, но недостаточным. Условие Стодола: Для устойчивости системы необходимо (но недостаточно), чтобы все коэффициенты характеристического уравнения были положительны (одного знака). Это условие будет необходимым и достаточным для уравнений 1 и 2 порядков. Запасы устойчивости
Этой ситуации не возникнет, если САР работает не вблизи границе устойчивости. А в достаточном удалении от нее. Иначе говоря, САР должна обладать некоторым запасом устойчивости, обеспечивающим работоспособность ее в различных условиях эксплуатации. Так как устойчивость замкнутой системы оценивается критерием Найквиста по расположению АФХ разомкнутой системы относительно критической точки, то в качестве меры оценки запаса устойчивости можно принять расстояние между АФХ Wp(jω) и критической точки (-1, j0). Но положение АФХ Wp(jω) на комплексной плоскости для каждого значения частоты ω характеризуется фазой и модулем. Именно поэтому вводят понятия запасов устойчивости те модулю (амплитуде) и фазе. Под запасом устойчивости по амплитуде понимают линейное отстояние точки АФХ разомкнутой системы с фазой = -1800 от критической точки (-1;j0).
С ростом Куст – запас устойчивости по амплитуде уменьшается.
Для устойчивых систем ЗУФ положителен γ>0. Для неустойчивых систем ЗУФ отрицателен γ1>0. С увеличением Кусил запас устойчивости по фазе уменьшается. Для хороших качественных систем γ =300 ÷ 600.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.70.203 (0.078 с.) |



 X2 Y2
X2 Y2

 :
:  , где р - число уравнений.
, где р - число уравнений.
 . Если число факторов больше 15, нужно обратиться к методам отсеивания несущественных факторов.
. Если число факторов больше 15, нужно обратиться к методам отсеивания несущественных факторов.


 Наилучшим условиям, определенным из анализа априорной информации соответствует комбинация (или несколько комбинаций) уровней факторов. Каждая комбинация является многомерной точкой в факторном пространстве. Ее можно рассматривать как исходную точку для построения плана эксперимента. Назовем ее основным уровнем. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня.
Наилучшим условиям, определенным из анализа априорной информации соответствует комбинация (или несколько комбинаций) уровней факторов. Каждая комбинация является многомерной точкой в факторном пространстве. Ее можно рассматривать как исходную точку для построения плана эксперимента. Назовем ее основным уровнем. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня.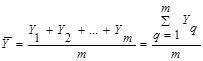
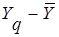 , где
, где  - результат отдельного опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений повторных опытов. Для измерения этой изменчивости чаще всего используют дисперсию. Дисперсия обозначается S2 и выражается формулой:
- результат отдельного опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений повторных опытов. Для измерения этой изменчивости чаще всего используют дисперсию. Дисперсия обозначается S2 и выражается формулой: 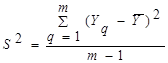 где (т -1) - число степеней свободы. Одна степень свободы использована для вычисления среднего (СКО):
где (т -1) - число степеней свободы. Одна степень свободы использована для вычисления среднего (СКО): 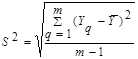
 Необходимо отметить, что наличие среди повторных опытов резко отличающихся результатов (грубых ошибок) может вызвать нарушение закона нормального распределения. Поэтому грубые наблюдения следует исключать, а затем рассчитывать среднее арифметическое и S2. Необходимо помнить, что даже такая простая операция, как вычисление среднего, требует определенных условий, в данном случае нормального распределения.
Необходимо отметить, что наличие среди повторных опытов резко отличающихся результатов (грубых ошибок) может вызвать нарушение закона нормального распределения. Поэтому грубые наблюдения следует исключать, а затем рассчитывать среднее арифметическое и S2. Необходимо помнить, что даже такая простая операция, как вычисление среднего, требует определенных условий, в данном случае нормального распределения. .
.


 .
. (1)
(1)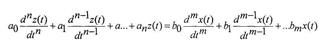 (2)
(2) (3) и частного вынужденного решения zвын (t)-вынужденная составляющая, т.е. то что остается после затухания свободной составляющей дифференциального уравнения z(t)=zсв(t) + zвын(t).
(3) и частного вынужденного решения zвын (t)-вынужденная составляющая, т.е. то что остается после затухания свободной составляющей дифференциального уравнения z(t)=zсв(t) + zвын(t). ;
; ;
;
 (4)
(4) (5)
(5)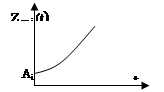
 , следовательно pi >0 – система неустойчива
, следовательно pi >0 – система неустойчива
 , следовательно pi <0 – система устойчива
, следовательно pi <0 – система устойчива
 - неустойчивая
- неустойчивая



 Признак устойчивости системы
Признак устойчивости системы Устойчивость является необходимым условием нормального функционирования САР. Если АФХ разомкнутой системы не охватывает критической точки (-1, j0), то САР в замкнутом состоянии устойчива (кривая 1 на рис. I), а если указанная АФХ проходит через т. (-1, j0), то замкнутая САР находится на границе устойчивости (кривая 2 на рис. I).
Устойчивость является необходимым условием нормального функционирования САР. Если АФХ разомкнутой системы не охватывает критической точки (-1, j0), то САР в замкнутом состоянии устойчива (кривая 1 на рис. I), а если указанная АФХ проходит через т. (-1, j0), то замкнутая САР находится на границе устойчивости (кривая 2 на рис. I). Отметим при этом, что чем ближе находится кривая 1 к критической точке (-1, j0), тем менее устойчивой становится замкнутая САР. Поскольку положение АФХ Wp(jω) на плоскости Гаусса определяется параметрами системы (коэффициентами усиления, постоянными времени и т.п. звеньев), то расположение кривых Wp(jω) вблизи притяжений точки может привести к ошибочным выводам об устойчивости САР. В самом деле, пусть в исходном состоянии параметры САР таковы, что отвечающая им кривая АФХ заняла положение 1. Однако, со временем в процессе эксплуатации параметры САР изменяются, и соответствующая этим измененным параметрам кривая Wp(jω) уже станет охватывать т. (-1,j0), т.е. займет положение 3. Это означает, что со временем, рассчитанная как устойчивая, САР станет неустойчивой.
Отметим при этом, что чем ближе находится кривая 1 к критической точке (-1, j0), тем менее устойчивой становится замкнутая САР. Поскольку положение АФХ Wp(jω) на плоскости Гаусса определяется параметрами системы (коэффициентами усиления, постоянными времени и т.п. звеньев), то расположение кривых Wp(jω) вблизи притяжений точки может привести к ошибочным выводам об устойчивости САР. В самом деле, пусть в исходном состоянии параметры САР таковы, что отвечающая им кривая АФХ заняла положение 1. Однако, со временем в процессе эксплуатации параметры САР изменяются, и соответствующая этим измененным параметрам кривая Wp(jω) уже станет охватывать т. (-1,j0), т.е. займет положение 3. Это означает, что со временем, рассчитанная как устойчивая, САР станет неустойчивой.

 - запас устойчивости по амплитуде. Для хороших систем (качественных)
- запас устойчивости по амплитуде. Для хороших систем (качественных)  Под запасом устойчивости по фазе понимаются угловое состояние точки АФХ разомкнутой системы с модулем =1 от критической точки -1;j0.
Под запасом устойчивости по фазе понимаются угловое состояние точки АФХ разомкнутой системы с модулем =1 от критической точки -1;j0.




