
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Этап учебного мозгового штурма: генерирование идей об оптимальном методе решения уравнений отдельных групп.
Необходимо для каждого типа уравнений найти оптимальный метод решения. Конечно, не всё удастся сделать за одну пару, но ведь и к крупным учёным момент озарения обычно приходит после долгих часов размышлений. На этом этапе своеобразными “ключами” нам послужат наиболее общие методы решения уравнений. Какие методы вы можете назвать? (Слайд № 7). Возможно, какие-то из этих методов применимы и к показательным уравнениям. Далее УМШ идёт по следующему алгоритму: 1. Выбор учащимися одного из типов уравнений; 2. 3-5 минутный мозговой штурм в группах (при этом уравнения не решаются до конца, а только генерируются “идеи” решения); 3. Выдвижение и обсуждение идей; 4. “Реализация” идеи – решение у доски (возможно, представителями разных групп одновременно, если идеи решения отличаются); запись решений в тетрадях; 5. Анализ решения, коррекция. Определение преимуществ и недостатков метода, его “тонких мест”, требований к оформлению. Запись решения в тетрадях. На этом этапе УМШ учителю нужно, не торопя учащихся, не отвергая ни одной идеи, не навязывая им свои методы, а лишь подсказывая направления поиска, поддерживать атмосферу “изобретательства”. При этом каждый “шаг” на пути поиска поощряется, а ошибки – анализируются, но не наказываются. Предполагается, что на этом уроке учащиеся найдут методы решения для первых четырёх типов (А, Б, В, Г). Методы решения этих уравнений общеизвестны (они сформулированы на слайдах №8 и №9). При решении уравнений группы В могут быть предложены два пути: традиционный – сведение при помощи замены переменной к дробно-рациональному уравнению, и более удобному - сведению к квадратному уравнению после домножения уравнения на подходящую степень. Например: № 4.(Задание из сборника для проведения письменного экзамена за курс средней школы [2]).
Домножим это уравнение на отличный от нуля множитель
Замена переменной
Полезно будет рассмотреть оба способа решения и позволить учащимся сравнить их преимущества и недостатки. При решении уравнений группы Д (№7, 12, 15) используется монотонность функций. Здесь надо обратить внимание на то, что, применяя этот метод, необходимо записать теоретическое обоснование этого решения. Рассмотрим уравнение №7 из сборника для проведения письменного экзамена [2], которое в некоторых пособиях предлагается решать как однородное уравнение третьей степени. Можно решить его, используя монотонность показательной функции:
степень 18x. При этом получим уравнение Уравнения группы Е (№9, 14, 16) содержат сопряжённые выражения. Обычно такие уравнения решаются умножением уравнения на одно из этих выражений (что проще) или заменой сопряжённых выражений на
Умножим это уравнение на
где после замены t=
t=4-
Ответ: -3;3. Уравнения группы Ж (№ 13, 19, 20) можно решить, используя ограниченность функций. В левой части уравнения №19 каждое слагаемое больше нуля, поэтому сумма больше нуля и уравнение корней не имеет. В уравнении №13
Решая это уравнение, полезно рассмотреть и графическую иллюстрацию. Ответы ко всем уравнениям Приложения1 содержатся в Приложении2. Незадолго до конца занятия, вне зависимости от количества рассмотренных типов уравнений, необходимо перейти к III этапу.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.104.238 (0.005 с.) |

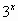 :
: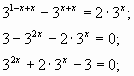
 t; t>0 приводит к уравнению типа Б:
t; t>0 приводит к уравнению типа Б: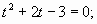
 или
или 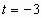 . Второй корень не удовлетворяет условию t>0.
. Второй корень не удовлетворяет условию t>0.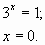
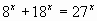 . Для применения метода монотонности необходимо, чтобы по одну сторону знака равенства стояла возрастающая функция, а по другую – убывающая функция. Этого можно добиться, если разделить уравнение на отличную от нуля
. Для применения метода монотонности необходимо, чтобы по одну сторону знака равенства стояла возрастающая функция, а по другую – убывающая функция. Этого можно добиться, если разделить уравнение на отличную от нуля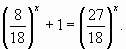 Далее необходимо сделать в тетрадях следующую запись: “функция у=
Далее необходимо сделать в тетрадях следующую запись: “функция у= 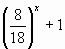 - возрастающая; функция у=
- возрастающая; функция у=  - убывающая, следовательно, данное уравнение имеет не более одного корня”. Этот корень находят подбором. В данном случае х=0 – корень. Проверка:
- убывающая, следовательно, данное уравнение имеет не более одного корня”. Этот корень находят подбором. В данном случае х=0 – корень. Проверка:  Ответ: 0. Надо отметить, что можно делить уравнение и на 27x. При этом слева от знака равенства получаем убывающую функцию, а справа – число 2. Тогда необходимо записать фразу “функция у=
Ответ: 0. Надо отметить, что можно делить уравнение и на 27x. При этом слева от знака равенства получаем убывающую функцию, а справа – число 2. Тогда необходимо записать фразу “функция у=  убывает и принимает каждое своё значение ровно один раз, следовательно, данное уравнение имеет не более одного корня”. Далее – аналогично рассмотренному случаю. Полезно добиться того, чтобы учащиеся “обнаружили” оба способа решения.
убывает и принимает каждое своё значение ровно один раз, следовательно, данное уравнение имеет не более одного корня”. Далее – аналогично рассмотренному случаю. Полезно добиться того, чтобы учащиеся “обнаружили” оба способа решения. и
и 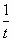 . Рассмотрим уравнение №16 из вступительного экзамена в РЭА им. Плеханова:
. Рассмотрим уравнение №16 из вступительного экзамена в РЭА им. Плеханова: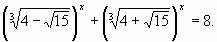

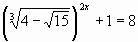
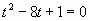 ;
;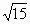 или t=4+
или t=4+  или
или

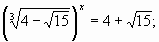
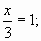

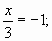

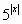
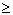 1, а 1-
1, а 1-  , поэтому равенство возможно только при условии
, поэтому равенство возможно только при условии 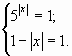 то есть, при х=0.
то есть, при х=0.


