
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Теоретические основы активного и интерактивного обученияСтр 1 из 10Следующая ⇒
Введение
Развивающемуся обществу нужны образованные, нравственные, предприимчивые, мобильные люди, способные самостоятельно принимать ответственные решения. Сегодня стало очевидным, что надо управлять не личностью, а процессом ее развития. В результате возникла необходимость обновления всей системы образования, что находит свое отражение в разработке и введении в практику работы школы элементов нового содержания, новых образовательных технологий. Сегодня многие методические новации и инновации связаны с реализацией интерактивного обучения, поскольку именно такое обучение обладает большими потенциальными возможностями для выполнения социального заказа современного общества. Глава 1. Теоретические основы активного и интерактивного обучения История возникновения активных и интерактивных методов обучения
Идеи активизации обучения высказывались учёными на протяжении всего периода становления и развития педагогики задолго до оформления её в самостоятельную научную дисциплину. К родоначальникам идей активизации относят Я. А. Коменского, Ж.-Ж. Руссо, И. Г. Песталоцци, Г. Гегеля, Ф. Фрёбеля, А. Дистервега, Дж. Дьюи, К. Д. Ушинского и других. Однако идеи, получившие наиболее последовательное изложение в работах данных авторов, берут своё начало из высказываний учёных и мыслителей античного мира. Всю историю педагогики можно рассматривать как борьбу двух взглядов на позицию ученика. Приверженцы первой позиции настаивали на исходной пассивности ученика, рассматривали его как объект педагогического воздействия, а активность, по их мнению, должен был проявлять только преподаватель. Сторонники второй позиции, среди которых был Пифагор, Демокрит, Сократ, Платон, Сенеки, Квинтилиан, считали ученика, равноправным участником процесса обучения и отдавали его активности главенствующую роль в обучении. В России использование активных и интерактивных методов широко практиковалось в 20-х гг. ХХ в. (проектный, лабораторно-бригадный метод, производственные, трудовые экскурсии, практики). Дальнейшая разработка этих методов присутствует в трудах Сухомлинского (60-егг.), а также в трудах Шаталова, Амонашвили, Лысенковой и других. Большую роль сыграла пропаганда игровых методов как основы активного обучения, и личное участие в создании и развитии игротехнического движения. Так возникли «Школы МАО», которые позволили ознакомить многих преподавателей с игровыми технологиями активного обучения, дать им первичные знания, навыки, «вооружить» первичным инструментарием.
В последние десятилетия ХХ в. проводились многочисленные эксперименты и научные исследования в области интерактивных методов, и были разработаны детальные руководства для учителей. Все эти методы и наработки способствуют активному использованию интерактивных средств в массовой школе. Методы обучения математике
Успех образовательного процесса во многом зависит от применяемых методов обучения. Методы обучения – это способы совместной деятельности педагога и учащихся, направленные на достижение ими образовательных целей. Методы являются одним из механизмов, способов осуществления педагогически целесообразного взаимодействия преподавателя и учащихся. Сущность методов обучения рассматривается как целостная система способов, в комплексе обеспечивающих педагогически целесообразную организацию учебно-познавательной деятельности учащихся. Таким образом, понятие метода обучения отражает во взаимосвязи способы и специфику обучающей работы преподавателя и учебной деятельности учащихся по достижению целей обучения. В современной педагогической практике используется большое количество методов обучения. Поэтому при подготовке к уроку у учителей часто возникают трудности, так как они не могут выбрать наиболее эффективные методы. В связи с этим возникает потребность в классификации, которая помогает выявить в методах обучения общее и особенное, существенное и случайное и тем самым способствует целесообразному и более эффективному их использованию. Единой классификации методов обучения не существует. Наиболее распространенные классификации методов обучения представлены в учебниках…. В связи с введением новых стандартов основной школы на первый план выходит классификация методов обучения по уровню активности учащихся. Согласно этой классификации методы обучения делятся на пассивные, активные и интерактивные.
К пассивным относятся методы, при которых учащиеся только слушают и смотрят (рис. 1). К ним относится рассказ, лекция, объяснение, экскурсия, демонстрация, наблюдение.
Рисунок 1 Активные методы — методы, организующие самостоятельную работу учащихся (рис. 2). К ним относятся следующие методы: лабораторный метод, практический метод, работа с книгой, научно-исследовательская работа.
Рисунок 2 Организация интерактивного обучения предполагает моделирование жизненных ситуаций, использование ролевых игр, общее решение вопросов на основании анализа обстоятельств и ситуации (лекции с проблемным изложением, эвристическая беседа, уроки семинары, конференции, деловые игры, использование средств мультимедиа, технология полноценного сотрудничества, метод проектов).Использование интерактивных методов обучения позволяет организовать самостоятельную познавательную деятельность в процессе урока (рис. 3).
Рисунок 3 Игра как метод
Математические игры имеют познавательное значение, поэтому в них на первый план выдвигается задача, для решения которой в мыслительной деятельности должны использоваться сравнения, анализ и синтез, суждения и умозаключения. 1. Основные задачи Конкурса по решению головоломок– повышение интереса учащихся к предмету; развитие логического мышления; приобретение школьниками опыта участия в соревнованиях. 2. Участники Конкурса– команды численностью 4 человека. 3. Всем командам-участникам Конкурса выдается одинаковый набор различных заданий, на решение которых дается 30-40 мин. 4. За правильное решение задания (ответ) начисляется его стоимость в баллах, за неправильное решение (ответ) – снимается половина стоимости задания в баллах. Игры, которые обычно используют на уроках математики: · «Морской бой» - излюбленная игра младших и старших школьников. Игровое поле – квадрат, состоящий из 10 столбцов и 10 строк. Координаты цели определяются именем столбца и строки. В эту игру играют три команды. Одно поле на все команды. Все клетки кораблей закрашены. Клетки, касающиеся бортов корабля, обозначены буквой, соответствующей теме вопроса. Участникам необходимо овладеть всеми кораблями. По очереди команды делают выстрелы. Ведущий открывает указанный квадратик. Если под ним окажется одна из палуб корабля, то этой команде сразу же начисляется 1 очко и дается право следующего хода. Если под ним окажется буква, то это значит, что рядом находится борт корабля. Команде задается соответствующий вопрос на обдумывание которого дается 30 сек. Если команда ответила не верно, то ответ может дать другая команда, кто быстрее, цена верного ответа – 2 очка, третьей попытки нет. Если никто не смог дать верного ответа, то ход переходит следующей команде. Если поле чистое – переход хода. · «Своя игра». В игре участвуют 3-5 команд, которые с экрана выбирают тему вопроса и его стоимость. Победителем считается команда, набравшая наибольшее количество баллов. · «Математический банкир». Класс делится на команды (лучше по два человека), каждая из которых представляет банк (президент банка и его заместитель). На столе разложены карточки с заданиями в перевернутом виде, каждая карточка имеет стоимость от 50 до 300 условных единиц в зависимости от сложности задачи. Это возможные вклады, инвестиции и т. д. Стартовый капитал каждого банка – 500 условных единиц Выбрав карточку с заданием и решив задачу, банк пополняет свой капитал на указанную сумму, если задача решена верно и терпит убытки на указанную сумму, если решение не верное. Ирга идет в течении урока или двух. В конце подводятся итоги – по капиталам банка.
Эту игру можно использовать при отработке навыков решения заданий по какой-либо теме. Дает возможность ребятам работать в своем темпе и выбирать свой уровень сложности заданий по данной теме. · Математический брейн-ринг. Основная цель этой игры – создать для школьника ситуацию, когда ему надо правильно и быстро решить задачу. К началу игры ведущий должен иметь некоторый список задач, к которым указаны ответы. Школьники разбиваются на команды. Каждой команде выдается листок, на котором она будет записывать ответы. Далее разыгрываются задачи. Разбор каждой происходит так: 1. Ведущий выдает (или просто читает) условие задачи командам, после чего они приступают к решению. 2. Сразу объявляется цена задачи по системе «баллы за ответ» + «баллы за решение». 3. Как только команда нашла ответ задачи, она его записывает на листочке и сдает ведущему. 4. Ведущий собирает ответы, учитывая порядок их поступления. 5. Решение задачи прекращается, когда собраны ответы от большей части команд. 6. Команды, которые дали верные ответы, получают «баллы за ответ». Команда, первой ответившая правильно, получает право рассказать решение. Решение оценивается по принципу «есть или нет»: команда получает либо все «баллы за решение», либо ничего. Общее количество использованных задач зависит от затраченного времени и заранее не объявляется. Когда розыгрыш задач закончен, подводится итог. Победителем признается команда, набравшая наибольшее число баллов. Все эти игры можно использовать как на уроке, так и во внеурочное время. Внеурочная работа по математике предоставляет школьникам дополнительные возможности для развития способностей, прививает интерес к математике. Главное назначение внеклассной работы – не только расширение и углубление теоретического материала, изученного на уроках, но и развитие умений применять полученные на уроках знания к решению – нестандартных задач, воспитанию у учеников определенной культуры работы над задачей и развития интеллектуального потенциала каждого ученика.
Обучение в малых группах Обучение в малых группах использовалось в педагогике довольно давно. Здесь очень важен эффект социализации, формирования коммуникативных умений. Ребята учатся вместе работать, учиться, творить, всегда быть готовыми прийти друг другу на помощь. Главная идея обучения в малых группах — учиться вместе, а не просто что-то выполнять вместе. Существует несколько условий для эффективной организации работы в малых группах. Прежде всего, ученики должны владеть знаниями и умениями для выполнения задания. В каждой группе ученик играет определённую роль, которую ему выбирает учитель (спикер, секретарь, посредник, докладчик). Каждая группа получает задания и чёткие инструкции по его выполнению. При этом учитель должен помогать в организации работы групп, не привлекая на себя особого внимания. При подведении итогов работы ученики предлагают результаты работы. Учителем комментируется работа групп с точки зрения учебных задач. В конце каждого занятия ученики высказывают свое мнение о предложенной форме работы. Интерактивная экскурсия Занятие-экскурсия – это такая форма обучения, при которой обучающиеся воспринимают и усваивают знания на месте расположения изучаемых объектов (природы, предприятия, музеи, выставки, исторические места и памятники и т.д.) и непосредственного ознакомления с ними. Главное преимущество виртуальных экскурсий – не покидая аудитории ознакомиться с объектами, расположенными за пределами кабинета, города и даже страны. В ходе экскурсии зрители не только видят объекты, на основе которых раскрывается тема, слышат об этих объектах необходимую информацию, но и овладевают практическими навыками самостоятельного наблюдения и анализа. Видеоконференция Методикой интерактивного занятия в форме видеоконференции является конференция. Визуализация и использование видеоконференцсвязи относится к использованию информационно- коммуникативных технологий в образовании. Данный формат проведения встречи позволяет объединить участников не только из разных городов, но и из разных стран, что, безусловно, способствует обмену опытом. 5.5. Социально-психологический тренинг Социально-психологический тренинг – это интерактивная форма обучения, целью которой является формирование недостающих поведенческих навыков и умений. Эта форма групповой работы позволяет работать с жизненными ситуациями. Тренинг как форма групповой работы позволяет использовать самые разнообразные интерактивные технологии. Фокус группа Фокус группа – это сообщество людей, объединенных в группы по каким-то критериям, в результате чего в ходе групповой дискуссии продуцируются данные, имеющие качественный характер. Длительность фокус группы обычно не превышает 2 часов. Фокус группы проводятся в специально оборудованных помещениях, оснащенных записывающей аудио и видео техникой, совмещенных с комнатой для скрытого наблюдения за процессом дискуссии.
Метод портфолио Метод Портфолио – один из тех методов, который растянут во времени, так как результат формируется к окончанию курса обучения, либо отдельной темы. Каждый ученик самостоятельно отслеживает и фиксирует результаты обучения, формируя из них своего рода учебную и творческую копилку. В связи с развитием информационно-коммуникационных технологий такая копилка формируется либо на сайте учебного заведения, либо в социальных сетях. Метод проектов Метод проектов – выполнение индивидуального или группового творческого проекта, по какой – либо теме. В данном методе учащиеся: самостоятельно и охотно приобретают недостающие знания из разных источников; учатся пользоваться приобретенными знаниями для решения познавательных и практических задач; приобретают коммуникативные умения, работая в различных группах; развивают исследовательские умения (умения выявления проблем, сбора информации, наблюдения, проведения эксперимента, анализа, построения гипотез, общения); развивают системное мышление. Сократический диалог Сократический диалог построен на задавании особым образом сформулированных, «наведенных» (но не наводящих) вопросов, он имеет давние традиции в преподавании. Данная методика может использоваться в научно-исследовательской работе, в учебном процессе и в практической деятельности. Возможна также организация преподавания в форме отдельных самостоятельных тренингов. Методика «Займи позицию» Обсуждение начинается с постановки дискуссионного вопроса, предполагающего взаимоисключающие ответы (например, «Вы за или против отмены смертной казни?»). Все участники, подумав над вопросом, подходят к одной из четырех табличек, размещенных в разных частях аудитории: ü Абсолютно за ü Абсолютно против ü Скорее за ü Скорее против ü Полностью согласен ü Полностью не согласен ü Скорее согласен ü Скорее не согласен Заняв позицию, участники обмениваются мнениями по дискуссионной проблеме и приводят аргументы в поддержку своей позиции. Любой участник может свободно поменять позицию под влиянием убедительных аргументов. Использование этой методики позволяет выявить имеющиеся мнения, увидеть сторонников и противников той или иной позиции, начать аргументированное обсуждение вопроса. Групповое обсуждение Групповое обсуждение какого-либо вопроса направлено на нахождении истины или достижение лучшего взаимопонимания. Групповые обсуждения способствуют лучшему усвоению изучаемого материала. На первом этапе группового обсуждения ставится проблема, выделяется определенное время, в течение которого ученики должны подготовить аргументированный развернутый ответ. На втором этапе группового обсуждения вырабатывается совместно с учителем групповое решение. Методика «Дерево решений» 1. Использование методики «дерево решений» позволяет овладеть навыками выбора оптимального варианта решения, действия и т.п. 2. Построение «дерева решений» – практический способ оценить преимущества и недостатки различных вариантов. Дерево решений для трех вариантов может выглядеть следующим образом: Проблема: …
Методика «Попс-формула» 1. Использование методики «ПОПС – формула» позволяет помочь студентам аргументировать свою позицию в дискуссии. 2. Краткое выступление в соответствии с ПОПС – формулой состоит из четырех элементов:
Лабораторный метод Одним из примеров активного метода обучения является лабораторный метод. В его основе лежит самостоятельное проведение исследований и экспериментов учащимися. Рассмотрим, как применяется данный метод в 9 классе при изучении правильных многоугольников.
Тема урока: Построение правильных многоугольников. Вид урока: Лабораторная работа. Цель: Научить строить некоторые правильные многоугольники. Задачи: 1. Закрепить навыки работы с чертежными инструментами; 2. Воспитать аккуратность и точность при выполнение чертежей; 3. Развить умения и навыки построения правильных многоугольников. Ход урока Третий этап С помощью полученных построений ученики должны самостоятельно записать алгоритмы построения правильных многоугольников и сделать вывод о том, какой из данных способов построения наиболее эффективный. Четвертый этап Все полученные выводы обобщаются и записываются на доске. Каждый записанный алгоритм обсуждаются, выявляются его положительные и отрицательные аспекты. После этого ученики самостоятельно для себя выбирают тот алгоритм построения правильных многоугольников, который кажется для них наиболее эффективным. Домашнее задание Выполнить построение правильного шестиугольника, восьмиугольника, шестнадцатиугольника на чертёжных листах. Подведение итогов урока Обобщение всех полученных результатов с помощью вопросов 1. Какие сложности вы испытывали при изучении и построении правильных многоугольников? 2. Каковы критерии эффективности их построения? 3. Где и зачем пригодятся эти умения и знания?
Таким образом, ученики, в ходе выполнения данной лабораторной работы могут сделать самостоятельные выводы. Задача учителя на таком уроке – проследить, чтобы эти выводы не были неправильными. Так, например, ученики могут предположить, что если дан правильный n - угольник, то с помощью циркуля и линейки всегда можно построить правильный 2n - угольник. Задача учителя здесь заключается в том, чтобы объяснить, что не все правильные многоугольники допускают такое построение и по возможности привести примеры. Лабораторная работа может проводиться как индивидуально, так и в группах. Например, при изучении в 7 классе темы «Равнобедренный треугольник и его свойства», класс можно провести лабораторно-исследовательскую работу, разбив класс на группы по четыре человека. Каждой группе дать карточки с заданиями, при выполнении которых ученики смогут совместно, в результате обсуждения прийти к определенным выводам. Рассмотрим примеры таких заданий. Задание 1. Постройте равнобедренный и равносторонний треугольники. Задание 2. Вырежьте их. Определите методом сгибания количество равных сторон. Равнобедренный треугольник – это … Равносторонний треугольник – это … Задание 3. Измерьте стороны треугольников, запишите данные в таблицу, сделайте выводы.
1) АВ = ___см; BC = ___см; AC = ___см; 2) MN = ___см; NK = ___см; MK = ___см; 3) ST = ___см; TR = ___см; SR = ___см; 4) DE = ___см; EF = ___см; DF = ___см; 5) OQ = ___см; QG = ___см; OG = ___см. Равные стороны равнобедренного треугольника называются боковыми, а третья сторона – основанием. В каждом равнобедренном треугольнике найдите боковые стороны и основание: 1) ∆АВС – боковые стороны:________; основание ____; 2) ∆MNK – боковые стороны:________; основание ____; 3) ∆STR – боковые стороны:________; основание ____. Таким образом, треугольники ∆ABC, ∆MNK, ∆STR - … (какие?). Сравните результаты измерений и дайте определение равнобедренного треугольника: Треугольник называется равнобедренным, если … Треугольник ∆OQG – ________________. Посмотрите на результаты измерений, дайте определение равностороннего треугольника: Треугольник называется равносторонним, если … Можно ли равносторонний треугольник назвать равнобедренным? Ответ: ___. А равнобедренный – равносторонним? Ответ: ___. Доказательство свойства Практический метод Практический метод очень похож на лабораторный. Он отличается от лабораторного метода только тем, что учащиеся применяют на практике те знания, которыми они уже владеют. То есть ученики должны показать свое умение использовать на практике теоретические знания. Практический метод способствует углублению знаний и умений, улучшает качество решения задач. В практическом методе выделяют следующие этапы: сначала учитель знакомит учащихся с теорией, затем идет инструктаж, после чего учитель показывает пример, как нужно делать (проба), затем идет выполнение работы, а потом контроль. Рассмотрим применение практического метода. Содержание кейса Задание: Вам наверно кажется, что геометрия совершенно не связана с нашей жизнью, что это очень трудная и непонятная наука. На самом же деле мы с вами живем в мире, который неразрывно связан с геометрией. Сегодня вам предстоит взглянуть на этот предмет совершенно с другой стороны. Желаю успехов и увлекательной работы! Проблема: зачем мы изучаем тему «Симметрия в пространстве», если не видим ее применение в жизни? Но зачем же тогда люди с древних времен изучают её. Даже говорят, что во всем в жизни есть симметрия. Цель: Организовать поиск, сбор и изучение информации по теме «Симметрия в пространстве» и ответить на вопрос: «Разве во всем в жизни есть симметрия?» Класс делится на 2 группы, каждая группа получает задачу: Группа 1: Задача. Сделайте вывод: «Есть ли симметрия в архитектуре, строительстве и искусстве?» Исследование проведите по схеме: 1. В качестве объектов исследования возьмите дома на улице, здания церквей, мост, орнамент, картину. 2. Рассмотрев данные объекты, ответьте на вопросы: обладают ли они симметрией? (Объясните свой ответ) 3. Добавьте и исследуйте свои объекты. Результаты исследования запишите в таблицу по форме:
Если объекты обладают симметрией, то укажите вид симметрии, если нет, то укажите – почему вы так считаете. Запишите, в чем вы видите Объекты исследования: 1. Мост; 2. Из предложенных объектов исследования выберите еще 7 объектов, которые вы хотите исследовать. Сделайте общие выводы по плану: 1. Симметрична ли общая форма всех выбранных объектов? 2. Присутствует ли точное сходство в деталях выбранных объектов? 3. Существует ли симметрии в архитектуре, строительстве, искусстве. Используют ли люди в архитектуре, строительстве, искусстве понятие симметрии? (Объясните свой ответ) Группа 2 Задача. Докажите или опровергните слова: «Сама природа подсказывает нам идею симметрии». Исследование проведите по схеме: 1. В качестве объектов исследования возьмите овощ, фрукт, лист дерева, дерево, гриб. Для детального изучения некоторых объектов можно воспользоваться лупой. 2. Рассмотрев данные объекты, ответьте на вопросы: обладают ли они симметрией? (Объясните свой ответ) 3. Добавьте и исследуйте свои объекты – животное, цветок, насекомое. Результаты исследования запишите в таблицу по форме:
Если объекты обладают симметрией, то укажите вид симметрии, если нет, то укажите – почему вы так считаете. Запишите, в чем вы видите Объекты исследования: 1. Гриб; 2. Из предложенных объектов исследования выберите еще 7 объектов, которые вы хотите исследовать. Сделайте общие выводы по плану: 1. Симметрична ли общая форма всех выбранных объектов? 2. Присутствует ли точное сходство в деталях выбранных объектов? 3. Существует ли симметрия в природе? Верно ли утверждение: «Идею симметрии подсказывает сама природа»? Нужна ли живым организмам симметрия? Таким образом, суть кейс-метода заключается в создании специально разработанных методических материалов в специальный набор (кейс) и их передаче обучающимся. Каждый кейс представляет собой полный комплект учебно-методических материалов, которые разрабатываются на основе конкретных ситуаций, способствующих формированию у обучающихся навыков самостоятельного решения конкретных задач. Мозговой штурм Организационный момент. Учащимся сообщается форма урока (УМШ), для создания творческой обстановки приводятся в качестве эпиграфа слова В.Гюго (Слайд №1): “Ум человеческий имеет 3 ключа, всё открывающих,- · знание; · мысль; · воображение”. Формируются творческие группы; записывается в тетрадях тема урока (Слайд №2). Актуализация знаний. Итак, первый “ключ” - знания. Учащиеся отвечают на вопросы: · Какими свойствами обладает показательная функция? · Какие методы решения показательных уравнений вам уже известны? (Приведение левой и правой части уравнения к степеням с равными основаниями; применение основного свойства пропорции; графический метод). · Применяя эти методы, решите устно уравнения (Слайд №3): Ответы: Сообщение цели урокаи постановка задачи УМШ. (Слайды №4,5). Рассмотренные в устной работе типы уравнений не исчерпывают всего многообразия показательных уравнений. Цель сегодняшнего урока и задача УМШ – отыскание методов решения других типов показательных уравнений. В этом вам помогут 3 ключа (каких?) и, конечно, интуиция. По мнению Спинозы, именно интуиция является высшим типом познания. Этапы учебного мозгового штурма (Слайд №6). Заключительная часть урока. На этом этапе необходимо коротко проанализировать работу каждой группы – активность, слаженность, корректность, умение преподносить свои идеи и принимать чужие. Обязательно надо отметить лучших “генераторов идей”. Я считаю, что на уроках УМШ нет необходимости ставить отметки, ведь оценить творчество в пятибалльной системе очень трудно.
Своя игра» Цель: обобщить и систематизировать полученные знания по математике Задачи: 1. Повышение познавательного интереса к предмету математики. 2. Воспитание у учащихся толерантности, умения работать в команде, выслушивать собеседника. 3. Развитие кругозора учащихся, логического мышления, математической речи и грамотности. Оборудование: доска, мел, тряпка, цветные жетончики, ноутбук, проектор, презентация. Структура воспитательного мероприятия: 1. Организационный момент (5 мин.); 2. Первый тур игры «Турнир знатоков» (15 мин.); 3. Второй тур игры «Турнир знатоков» (15 мин.); 4. Финал игры (2 мин.); 5. Викторина (5 мин.); 6. Подведение итогов (3 мин.). Ход: Организационный момент Ведущий: Здравствуйте, ребята! Сегодня нам представилась замечательная возможность принять участие в увлекательнейшей викторине «Своя игра». В конце этой игры мы обязательно узнаем, в какой команде собрались самые настоящие знатоки, какая команда окажется самой дружной и активной, а также кто в нашем классе самый эрудированный и знает ответы на все вопросы. Для этого мы разделились на 3 команды. (Перед мероприятием ученики должны были вытянуть одну из четырех цветных карточек: желтую, красную или фиолетовую. За каждой карточкой был закреплен свой номер: желтая - №1, красная - №2, фиолетовая - №3. Войдя в класс, ученики садились за один из трех столов, за каждым из которых был закреплен свой цвет.) Сейчас в течение двух минут вы должны будете выбрать капитана и придумать название своей команде. (В течение двух минут учащиеся обсуждают название команды и назначают капитана). Хорошо! Теперь каждый из капитанов должен представить свою команду. Начнем с команды №1, т.е. с желтой команды (далее свои команды представляют капитаны красной и фиолетовой команд). Капитан 1: Наша команда называется «…». Капитан 2: Название нашей команды – «…». Капитан 3: Мы назвали нашу команду «…». Ведущий: Отлично! А теперь давайте обсудим правила игры. Будьте внимательны! Итак, «Своя игра» играется в 2 тура. В первом туре командам предстоит ответить на вопросы следующих блоков: «Задачи», «Интересные факты», «Логика». Во втором туре участников ждут вопросы по следующим блокам: «Числа», «Планиметрия» и «Уравнения». Кроме того, после этих двух туров проводится финальная игра, которая определит победителя. На каждую область мы приготовили по пять вопросов: легкий, который оценивается в 100 баллов, вопрос средней сложности стоимостью 200 баллов, в 300 баллов оценивается правильный ответ на более сложный вопрос и, наконец, ответ на самый сложный вопрос прибавит в вашу копилку 400 баллов. Каждая команда имеет право выбрать вопрос любой сложности из представленных блоков (если этот вопрос еще не был выбран). Право выбора первого вопроса представляется игрокам желтой (первой) команды. После того, как будет дан ответ на первый вопрос, свои вопросы выбирают участники красной (второй) команды, затем – фиолетовой (третьей). Время на обдумывание ответа – 60 сек. Затем отвечает капитан (именно он!) той команды, которая выбрала вопрос. За каждый правильный ответ вы получаете то количество баллов, которым оценен вопрос. Если у команды нет ответа, то ответить на вопрос могут участники других команд; за правильный ответ им начисляется заявленное количество баллов. Нарушение дисциплины наказывается, у команды вычитается 100 баллов! Правильность ответов оценивает наше уважаемое жюри (в члены жюри назначить присутствующих на мероприятии наблюдателей)! В нашей игре участников ждут небольшие сюрпризы – вопрос-аукцион и кот в мешке. На вопрос-аукцион право ответа имеет та команда, которая назначит большую сумму (от 100 до 400 баллов), если на счету игроков сумма, меньшая чем стоимость вопроса, то они могут предложить только номинал (стоимость вопроса). На вопрос кот в мешке отвечает та команда, которой отдает это право команда, выбравшая вопрос. Победитель определится в финале нашей игры, в котором участие принимают только две команды, набравшие большее количество баллов. В финале участникам команд предлагается выбрать один из трех блоков: «Шифровка», «Теорема» или «Проценты», а затем устно ответить на 1 вопрос выбранного блока. Ведущий: Игроки, ваши вопросы? Участники команд задают имеющиеся у них вопросы. Ведущий: Ну что ж, в добрый путь, ребята! Финал игры Настало время познакомить участников с правилами финальной игры! Участникам двух оставшихся команд предлагается выбрать один из трех представленных блоков и устно ответить на один вопрос. Право ответа предоставляется капитану той команды, участники которой быстрее подняли руки. Время обдумывания ответа на вопрос – 2 мин. Ребята, есть ли у вас вопросы по финальной игре? Участники команд задают имеющиеся у них вопросы. Ученик 1: Шифровка Ведущий: Отлично! В добрый путь, ребята! Внимание финальный вопрос: … Игроки отвечают на финальный вопрос (Приложение 1). Ведущий: Время истекло. Ваш ответ на вопрос? Игроки дают ответ на вопрос. Викторина Ведущий: Ну что ж, настало время подвести окончательный итог нашей игре. Пока наше уважаемое жюри подводит итоги игры, мы тем временем попытаемся выяснить, есть ли в нашем классе эрудит, который знает ответы на вопросы из самых разных областей знания. Участники викторины, знающие ответ на тот или иной вопрос, должны поднять руки (спрашивать тех, кто быстрее поднял руку). Не забываем о дисциплине! Если ответ не верен, слово предоставляется другим участникам (тем, кто поднял руки вторыми, третьими и т.д.). За каждый правильный ответ вы получаете жетончик. У кого жетончиков больше – тот и победил. Итак, ребята, вам понятны правила? Участники команд: Да! Ведущий: В таком случае приступим. Внимание, первый вопрос! Во время подведения итогов участники игры принимают участие в викторине. 1. На острове Самос Философ сей родился. И во главу угла Поставлены им числа. И, говорят, за теорему Принес богам быка он в жертву. Был чемпионом Олимпиады, Имел своих учеников. Надеюсь, догадался каждый, Что его имя … (Пифагор) 2. Два бизнесмена поспорили: кто получил больше прибыли. Один выручил от продажи своих товаров 5000 т., а его расходы составили 3000 т. Другой наторговал на 1000т. меньше, но и затратил своих денег всего 2000 т. Кто выиграл спор? (Никто) 3. После того, как бегун пробежал треть всей дистанции и еще 400 м, ему осталось пробежать еще треть пути и еще 200 м. Чему равна длина дистанции? (1800 м) 4. Сколькими нулями заканчивается произведение натуральных чисел 1 × 2 × 3 × 4 × 5 × 6 × … × 100? (24) 5. Математики начала По обоям изучала И влюбилась в ту науку. Только вот какая штука. Ведь в России в это время Не пускали в вузы женщин. Чтоб в математике достичь вершин, Пришлось уехать девушке в Берлин, И стать для этого фальшивою
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 961; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.110.134 (0.187 с.) |





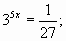








 0; 0; нет корней; 2;
0; 0; нет корней; 2; 



