
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практическая работа по теме «Призма. Куб»Содержание книги
Поиск на нашем сайте
1. Организационный момент Приветствие учителя. Учитель сообщает тему урока. 2. Актуализация знаний и изучение новой темы Учитель строит на доске объемную фигуру, все стороны которой равны и в основании лежит квадрат (рис. 4). Ученики должны назвать эту фигуру (куб). На примере куба учитель знакомит учеников с с понятием призмы, с элементами призмы (стороны, вершины, диагонали).
Рисунок 4 3. Практическая работа Учитель дает ученикам инструкции по выполнению практической работы: А) Сделайте рисунок куба (рис. 4) и обозначьте на нем вершины, ребро a, диагональ основания d и диагональ куба D. Б) Выведите формулы для вычисления диагонали основания d, диагонали куба D, периметра основания P, площади основания S, диагонали сечения Q. В) Запишите полученные формулы для вычисления этих элементов куба: d=______, D=______, P=______, S=______, Q=______. Г) Используя данные таблицы и опираясь на рисунок, найдите другие элементы куба. Заполните таблицу.
4. Подведение итогов Учитель собирает карточки с выполненными заданиями. Затем задает ряд вопросов, при помощи которых происходит закрепление и систематизация полученных знаний. Кроме рассмотренных выше методов в школе наиболее часто используют еще один – работу с книгой. В этом случае ученики должны самостоятельно изучить тему с помощью учебника или дополнительной литературы, а затем выполнить ряд заданий на изученную тему.
Методика интерактивного обучения на уроках математики
Интерактивный метод обучения состоит в организации учебного процесса таким образом, чтобы все ученики оказались вовлеченными в процесс познания. Причем происходить это должно в сфере доброжелательности и взаимной поддержки. Интерактивное обучение предполагает организацию и развитие диалогового общения, которое ведет к взаимопониманию, совместному решению общих задач. Рассмотри методику применения некоторых интерактивных методов. 2.1. Case-study (кейс-метод) Одним из наиболее эффективных и распространенных методов организации активной познавательной деятельности обучающихся является кейс-метод. В этом случае учащиеся сталкиваются с конкретной ситуацией. При этом они должны определить: есть ли здесь проблема, в чем она состоит, а также должны определить свое отношение к ситуации. Рассмотрим фрагмент урока по геометрии по теме «Многогранники» с применением кейс-метода. Кейс «Симметрия в пространстве» Содержание кейса Задание: Вам наверно кажется, что геометрия совершенно не связана с нашей жизнью, что это очень трудная и непонятная наука. На самом же деле мы с вами живем в мире, который неразрывно связан с геометрией. Сегодня вам предстоит взглянуть на этот предмет совершенно с другой стороны. Желаю успехов и увлекательной работы! Проблема: зачем мы изучаем тему «Симметрия в пространстве», если не видим ее применение в жизни? Но зачем же тогда люди с древних времен изучают её. Даже говорят, что во всем в жизни есть симметрия. Цель: Организовать поиск, сбор и изучение информации по теме «Симметрия в пространстве» и ответить на вопрос: «Разве во всем в жизни есть симметрия?» Класс делится на 2 группы, каждая группа получает задачу: Группа 1: Задача. Сделайте вывод: «Есть ли симметрия в архитектуре, строительстве и искусстве?» Исследование проведите по схеме: 1. В качестве объектов исследования возьмите дома на улице, здания церквей, мост, орнамент, картину. 2. Рассмотрев данные объекты, ответьте на вопросы: обладают ли они симметрией? (Объясните свой ответ) 3. Добавьте и исследуйте свои объекты. Результаты исследования запишите в таблицу по форме:
Если объекты обладают симметрией, то укажите вид симметрии, если нет, то укажите – почему вы так считаете. Запишите, в чем вы видите Объекты исследования: 1. Мост; 2. Из предложенных объектов исследования выберите еще 7 объектов, которые вы хотите исследовать. Сделайте общие выводы по плану: 1. Симметрична ли общая форма всех выбранных объектов? 2. Присутствует ли точное сходство в деталях выбранных объектов? 3. Существует ли симметрии в архитектуре, строительстве, искусстве. Используют ли люди в архитектуре, строительстве, искусстве понятие симметрии? (Объясните свой ответ) Группа 2 Задача. Докажите или опровергните слова: «Сама природа подсказывает нам идею симметрии». Исследование проведите по схеме: 1. В качестве объектов исследования возьмите овощ, фрукт, лист дерева, дерево, гриб. Для детального изучения некоторых объектов можно воспользоваться лупой. 2. Рассмотрев данные объекты, ответьте на вопросы: обладают ли они симметрией? (Объясните свой ответ) 3. Добавьте и исследуйте свои объекты – животное, цветок, насекомое. Результаты исследования запишите в таблицу по форме:
Если объекты обладают симметрией, то укажите вид симметрии, если нет, то укажите – почему вы так считаете. Запишите, в чем вы видите Объекты исследования: 1. Гриб; 2. Из предложенных объектов исследования выберите еще 7 объектов, которые вы хотите исследовать. Сделайте общие выводы по плану: 1. Симметрична ли общая форма всех выбранных объектов? 2. Присутствует ли точное сходство в деталях выбранных объектов? 3. Существует ли симметрия в природе? Верно ли утверждение: «Идею симметрии подсказывает сама природа»? Нужна ли живым организмам симметрия? Таким образом, суть кейс-метода заключается в создании специально разработанных методических материалов в специальный набор (кейс) и их передаче обучающимся. Каждый кейс представляет собой полный комплект учебно-методических материалов, которые разрабатываются на основе конкретных ситуаций, способствующих формированию у обучающихся навыков самостоятельного решения конкретных задач. Мозговой штурм Организационный момент. Учащимся сообщается форма урока (УМШ), для создания творческой обстановки приводятся в качестве эпиграфа слова В.Гюго (Слайд №1): “Ум человеческий имеет 3 ключа, всё открывающих,- · знание; · мысль; · воображение”. Формируются творческие группы; записывается в тетрадях тема урока (Слайд №2). Актуализация знаний. Итак, первый “ключ” - знания. Учащиеся отвечают на вопросы: · Какими свойствами обладает показательная функция? · Какие методы решения показательных уравнений вам уже известны? (Приведение левой и правой части уравнения к степеням с равными основаниями; применение основного свойства пропорции; графический метод). · Применяя эти методы, решите устно уравнения (Слайд №3): Ответы: Сообщение цели урокаи постановка задачи УМШ. (Слайды №4,5). Рассмотренные в устной работе типы уравнений не исчерпывают всего многообразия показательных уравнений. Цель сегодняшнего урока и задача УМШ – отыскание методов решения других типов показательных уравнений. В этом вам помогут 3 ключа (каких?) и, конечно, интуиция. По мнению Спинозы, именно интуиция является высшим типом познания. Этапы учебного мозгового штурма (Слайд №6).
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 931; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

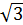


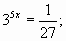








 0; 0; нет корней; 2;
0; 0; нет корней; 2; 



