
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Еквівалентні множини. Потужність множинСодержание книги
Поиск на нашем сайте Означення 1.22. Множини Множина Означення 1.23. Клас еквівалентних множин, якому належить множина Кажуть, що Наведемо основні властивості потужностей: 1) 2) 3) Розглянемо множину всіх підмножин множини Останнє твердження показує, що якщо нескінченні множини існують, то і „нескінченності” бувають різні. Потужність скінченної множини дорівнює кількості її елементів. Нескінченні множини, еквівалентні множині Наведемо основні властивості зчисленних множин. 1. Будь-яка нескінченна підмножина зчисленної множини є зчисленною множиною. 2. Якщо від зчисленної множини відкинути скінченну множину елементів, то потужність нескінченної множини, яка залишилась, буде 3. Зчисленна множина зчисленних множин є зчисленною множиною. 4. Об’єднання скінченної кількості зчисленних множин є зчисленною множиною. Множина
Потужність континуума Означення 1.24. Множину Відомо, що Вже на початку розвитку теорії множин виникло питання, чи існують множини проміжної потужності між зчисленними множинами і множинами потужності континуума, і було зроблено припущення, яке називають гіпотезою континуума, що проміжні потужності відсутні. В 1963 році американець Коен (I. Cohen) довів, що ця і протилежна гіпотези окремо не є протиріччям прийнятій в теорії множин аксіоматиці, а тому гіпотеза континуума не може бути ні доведена, ні заперечена.
Вправи 1.1. Нехай 1.2. Зобразити на координатній площині множини 1.3. Довести тотожності: а) в) д) є) ж) з) к) м) 1.4. З'ясувати яке з включень виконано а) б) в) г) д) 1.5. Знайти а) 1.6. Встановити взаємно-однозначну відповідність між множинами: а) в) г) д) є) множиною натуральних чисел і множиною парних натуральних чисел; ж) з) і) 1.7. Знайти потужності множин: а) б) множина точок в) множина кіл з раціональними координатами центру г) множина точок відрізка д) 1.8. Знайти точну верхню та точну нижню грані множин: а) в) г)
|
||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 і
і  називають еквівалентними, якщо за певним законом можна встановити взаємно-однозначну відповідність елементів. Еквівалентні множини позначають:
називають еквівалентними, якщо за певним законом можна встановити взаємно-однозначну відповідність елементів. Еквівалентні множини позначають: 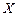 рівнопотужна множині
рівнопотужна множині  , якщо існує бієктивне відображення
, якщо існує бієктивне відображення  або
або  . Якщо
. Якщо  .
. , якщо
, якщо  рівнопотужна деякій підмножині множини
рівнопотужна деякій підмножині множини 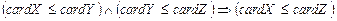 ;
;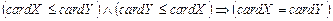 – теорема Шредера-Бернштейна (F. Schröder);
– теорема Шредера-Бернштейна (F. Schröder); – теорема Кантора.
– теорема Кантора. . Тоді справедлива теорема Кантора:
. Тоді справедлива теорема Кантора:  . Також можна стверджувати, що
. Також можна стверджувати, що  .
. , називаються зчисленними множинами, а їх потужність називають зчисленною потужністю і позначають
, називаються зчисленними множинами, а їх потужність називають зчисленною потужністю і позначають 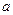 .
.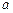 .
. ~
~  . Множина
. Множина  ~
~  .
. називають числовим континуумом, а його потужність – потужністю континуума. Потужність множини дійсних чисел позначають
називають числовим континуумом, а його потужність – потужністю континуума. Потужність множини дійсних чисел позначають  .
. (теорема Кантора). Доведення випливає з доведення незчисленності множини точок відрізку
(теорема Кантора). Доведення випливає з доведення незчисленності множини точок відрізку  . З теореми випливає, що
. З теореми випливає, що  і існують ірраціональні числа. Також відомо, що
і існують ірраціональні числа. Також відомо, що  .
. ,
,  ,
,  . З яких елементів складаються множини:
. З яких елементів складаються множини: 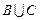 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 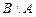 .
. , де
, де 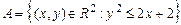 ,
,  .
.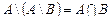 ; б)
; б)  ;
; ; г)
; г)  ;
; ;
;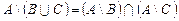 ;
; ;
; ; і)
; і)  ;
;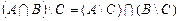 ; л)
; л) 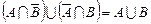 ;
; ; н)
; н)  .
. або
або  , або
, або  , якщо:
, якщо: ,
,  ;
;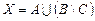 ,
,  ;
; ,
,  ;
; ,
, 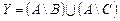 ;
; .
. ,
,  , якщо
, якщо , б)
, б)  , в)
, в)  .
. і
і  ; б)
; б) 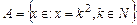 і
і 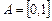 і
і  ;
;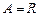 і
і  ;
; ;
; і
і  ;
; і
і  ;
; ;
; площини з раціональними координатами;
площини з раціональними координатами; (
( ,
, 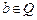 ) і радіусом
) і радіусом  ;
; , у яких у десятковому записі відсутня цифра 5;
, у яких у десятковому записі відсутня цифра 5; .
. ; б)
; б)  ;
; ;
; .
.


