
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування послідовностей в економіці
Розглянемо загальноприйняті в ринковій економіці алгоритми нарахування відсотків залежно від терміну позички, типу відсотків, схеми їхнього нарахування. Нехай спочатку була сума 1. Прості відсотки (у кожен часовий період на відсоток, що додається, нарахування не відбуваються):
2. Складні відсотки (відсоток доходу нараховується на всі грошові накопичення):
З останньої формули легко одержати:
Операція знаходження початкового внеску 3. Нехай відсотки нараховуються рівномірно
4. Нехай відсотки нараховуються неперервно, тобто
Цю формулу можна використовувати для будь-яких розрахунків з помилковими відсотками.
Поняття функції При вивченні будь-якого процесу (фізичного, хімічного, біологічного, економічного та інших) в оточуючому нас реальному світі нам доводиться зустрічатися з тими чи іншими величинами, які їх характеризують та змінюються. Залежно від розглянутих умов одні з цих величин приймають сталі значення, інші – змінні. Величина називається сталою, якщо в процесі дослідження її чисельне значення не змінюється. Наприклад, довжина кола обчислюється за формулою Величина, що набуває в даних умовах різні числові значення, називається змінною. Іноді сталу величину розглядають як змінну, усі значення якої збігаються. Часто в одному і тому процесі бере участь кілька змінних величин, причому зміна чисельного значення однієї з них приводить до зміни значень інших. У такому випадку говорять, що між зазначеними величинами існує функціональна залежність. Означення 2.5. Змінна
де Змінну x називають незалежною змінною, або аргументом функції, множину
Інакше кажучи, область визначення функції Змінну y називають залежною змінною або функцією, множину Функціональну залежність Запис Означення 2.6. Графіком функції
Способи задання функції Відповідно до означення, функція вважається заданою, якщо задана область визначення функції і правило (закон), що встановлює відповідність між значеннями незалежної змінної x і залежної змінної y. При цьому не накладається ніяких обмежень на характер цієї відповідності. Найчастіше функція задається за допомогою формули, що вказує, які дії треба виконати над аргументом, щоб одержати відповідне значення функції. Така формула називається аналітичним виразом, а спосіб задання функції за допомогою формули називається аналітичним способом задання функції. Наприклад, формула Функція, представлена формулою у вигляді
визначена на проміжку Якщо рівняння, що задає функцію, не розв’язане відносно залежної змінної
функція називається заданою неявно. Так, рівняння
Трапляються випадки, коли рівняння (2.2) не задовольняється жодною парою дійсних значень Аналітично представлена функціяназиваєтьсязаданою параметрично, якщо її аргумент
Якщо дано дві функції Наприклад, якщо Аналітичний спосіб задання функції компактний, легко відтворений і найбільш пристосований до виконання над функціями математичних дій. Часто при дослідженні будь-яких процесів доводиться зустрічатися зі змінними величинами, залежність між якими встановлюється експериментальним шляхом. У таких випадках на підставі експериментальних даних складають таблиці, що відповідають різним окремим значенням аргументу. Такий спосіб задання функції називається табличним. Знаючи аналітичний вираз функції, завжди можна представити цю функцію для цікавлячих нас значень аргументу таблицею. Говорять, функцію можна табулювати. Табулюються в основному функції, що мають складний аналітичний вираз, але часто зустрічаються на практиці. Помітимо, що від табличного задання функції не завжди можна перейти до її аналітичного виразу, насамперед таблиця дає не всі значення функції, і, потім, проміжні значення функції можуть бути знайдені лише приблизно. Проте, завжди можна знайти формулу, і не одну, котра для значень аргументу, що є в таблиці, з визначеною точністю буде давати відповідні табличні значення функції. Найбільш наочним способом задання функції
Щоб для зазначеного значення аргументу Графічне задання функції одержуємо за допомогою багатьох самописних приладів, наприклад, криві на осцилографі, барографі, кардіографі і т.д. З цих графіків для будь-якого моменту часу можна знайти (приблизно) значення функцій. Зазначені вище три способи задання функцій (аналітичний, табличний, графічний) є найбільш розповсюдженими, але не вичерпують усіх можливих способів завдання функції. Можна задати функцію за допомогою правила, що вказує які значення вона набуває для різних значень аргументу. Прикладом такої функції є функція Діріхле, обумовлена так: Зараз дуже широко застосовується ще один спосіб завдання функції – за допомогою програми для обчислення її значень на електронно-обчислювальних машинах (персональних комп'ютерах).
Деякі властивості функцій Однією з основних задач математичного аналізу є визначення властивостей функції.
Функція
і непарною, якщо
Прикладами парних функцій можуть бути функції Відзначимо, що функція може бути ні парною, ні непарною, наприклад, Неважко показати, що графіки парних функцій симетричні відносно вісі ординат, а графіки непарних функцій симетричні відносно початку координат. Функція Можна показати, якщо число Нулями функції називаються абсциси точок перетину графіка функції з віссю абсцис, тобто розв’язки рівняння Функція Відповідно функція Функція Відповідно функція Зростаючі, спадні, не зростаючі та не спадні функції називаються монотонними.
Функція, обернена до даної Нехай функція Припустимо, що задане рівняння розв’язане відносно Якщо, дотримуючись стандартних позначень, під
Функції
Якщо ж умовитися позначати незалежну змінну через Так, щоб знайти функцію обернену до
Класифікація функцій Розглянемо деякі класи функцій, що найбільш часто зустрічаються. 1. Многочлени або цілі раціональні функції. Многочленом називається функція виду:
де При При При 2. Дробово-раціональні функції. Дробово-раціональною функцією відносно
де Функція (2.4) визначена для всіх значень Функція 3. Алгебраїчні функції. Алгебраїчною називають функцію, одержану з аргументу Алгебраїчні функції, що не є раціональними, називаються ірраціональними, наприклад,
4. Трансцендентні функції. Трансцендентними функціями називаються усі функції, що не є алгебраїчними. До них належать показникові, логарифмічні, тригонометричні, обернені тригонометричні функції та ін. Показниковою називається функція виду Графіки показникових функцій для випадку
Рис. 2.7. Те значення a, при якому кут a між віссю Ox і дотичною до кривої Логарифмічна функція Як і показникова функція, найбільш прості властивості має логарифмічна функція з основою
Логарифми чисел з основою
Рис. 2.8.
Тригонометричні функції Функції Функція Функція
Рис. 2.9.
Рис. 2.10.
Рис. 2.11.
Рис. 2.12.
Оберненими тригонометричними функціями є функції Функція Якщо відомі всі значення
Аналогічно функція Функція визначена на відрізку [–1;1]. Якщо відомі всі значення y, косинус яких дорівнює На підставі властивостей дуг, що мають однаковий косинус, випливає формула:
Графіки функцій
Функція
Графік функції Функція Якщо врахувати всі значення
Графік функції зображений на рис. 2.16.
Будемо називати елементарними функціями степеневу, показникову, логарифмічну, тригонометричні і обернені тригонометричні. Функції, одержані з елементарних за допомогою скінченного числа алгебраїчних дій і скінченного числа операцій обчислення функції від функції, будемо називати елементарними функціями.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.235.104 (0.085 с.) |
 грош. од. Процентна ставка –
грош. од. Процентна ставка –  відсотків річних. Тоді після
відсотків річних. Тоді після  років одержимо наступні суми грошей.
років одержимо наступні суми грошей. .
.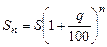 .
. ,
,  ,
, 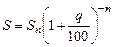 .
. . Різниця
. Різниця  називається дисконтом.
називається дисконтом.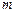 разів на рік. Тоді одержимо:
разів на рік. Тоді одержимо: .
. . Тоді одержимо границю послідовності:
. Тоді одержимо границю послідовності: .
. , де число p не залежить від розмірів кола.
, де число p не залежить від розмірів кола. називається функцією від змінної
називається функцією від змінної  , якщо кожному значенню
, якщо кожному значенню  за певним законом ставиться у відповідність єдине значення
за певним законом ставиться у відповідність єдине значення  . Тоді записують
. Тоді записують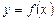 , (2.1)
, (2.1)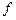 – закон, за яким кожному
– закон, за яким кожному  ставиться у відповідність значення
ставиться у відповідність значення  . Тобто можна казати, що задано функцію
. Тобто можна казати, що задано функцію  , де
, де  .
. . Тобто
. Тобто  .
. . Тобто
. Тобто 
 означає, що береться частинне значення функції
означає, що береться частинне значення функції  при
при 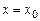 . Наприклад, для функції
. Наприклад, для функції  при
при  маємо частинне значення функції
маємо частинне значення функції 
 координатної площини
координатної площини  , координати яких задовольняють рівність, що задає функцію. Так, графіком функції
, координати яких задовольняють рівність, що задає функцію. Так, графіком функції  є парабола.
є парабола.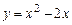 означає, що для того, щоб одержати значення функції
означає, що для того, щоб одержати значення функції  називається заданою аналітично явно. Функція іноді задається декількома формулами, що діють на різних ділянках зміни аргументу, наприклад, функція
називається заданою аналітично явно. Функція іноді задається декількома формулами, що діють на різних ділянках зміни аргументу, наприклад, функція
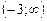 . Кожному значенню
. Кожному значенню  ,
,  і т.д.
і т.д. , (2.2)
, (2.2)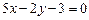 неявно задає
неявно задає  .
. . Рівняння може задовольнятися лише однією парою дійсних чисел, як наприклад, рівняння
. Рівняння може задовольнятися лише однією парою дійсних чисел, як наприклад, рівняння  задовольняється тільки значеннями
задовольняється тільки значеннями  ,
,  .
. , яку називають параметром:
, яку називають параметром:
 ,
, 
 ,
,  – дійсні числа.
– дійсні числа. і
і  , причому множина значень другої функції входить в область визначення першої, то
, причому множина значень другої функції входить в область визначення першої, то 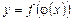 називається складною функцією змінної
називається складною функцією змінної 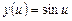 ,
,  , то
, то  – складна функція. Складними будуть функції
– складна функція. Складними будуть функції  ,
,  ,
,  і т.д.
і т.д. є графічний спосіб, коли відповідність між аргументом
є графічний спосіб, коли відповідність між аргументом  Рис. 2.1.
Рис. 2.1.
 :
:
 .
. і т.д. Відповідно непарними функціями є функції
і т.д. Відповідно непарними функціями є функції  ,
, 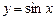 .
. ,
,  ,
,  та ін.
та ін. :
: 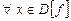
 . При цьому число
. При цьому число  , а функції
, а функції  ,
,  періодичні з періодом
періодичні з періодом  .
. (
( ) також є періодом цієї функції. Якщо функція
) також є періодом цієї функції. Якщо функція  періодична з періодом
періодична з періодом  . Справді,
. Справді,  . Наприклад, функція
. Наприклад, функція  періодична з періодом
періодична з періодом  , функція
, функція  періодична з періодом
періодична з періодом  . Розв’язати рівняння
. Розв’язати рівняння  іноді важко, що вимагає наближених методів.
іноді важко, що вимагає наближених методів. цього проміжку з умови
цього проміжку з умови  випливає, що
випливає, що 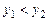 , тобто більшому значенню аргументу відповідає більше значення функції.
, тобто більшому значенню аргументу відповідає більше значення функції. випливає, що
випливає, що  .
. . Знайдена функція називається оберненою до функції
. Знайдена функція називається оберненою до функції  .
. .
. задають тим самим графіком, оскільки визначають ту саму функціональну залежність між x і y.
задають тим самим графіком, оскільки визначають ту саму функціональну залежність між x і y. Рис. 2.2.
Рис. 2.2.
 .
. і перемінимо місцями
і перемінимо місцями  , обернену до функції
, обернену до функції  , (2.3)
, (2.3) – сталі коефіцієнти многочлена,
– сталі коефіцієнти многочлена, 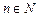 . Старший степінь змінної
. Старший степінь змінної  , то степінь многочлена (2.3) дорівнює
, то степінь многочлена (2.3) дорівнює  маємо многочлен нульового степеня
маємо многочлен нульового степеня  , де
, де  – число. Графік такої функції – пряма паралельна вісі
– число. Графік такої функції – пряма паралельна вісі 
 маємо многочлен першого степеня
маємо многочлен першого степеня  , його називають лінійною функцією. Графіком такого многочлена є пряма.
, його називають лінійною функцією. Графіком такого многочлена є пряма. маємо многочлен другого степеня
маємо многочлен другого степеня  , таку функцію називають квадратичною функцією. Графіком квадратичної функції є парабола з вертикальною віссю симетрії.
, таку функцію називають квадратичною функцією. Графіком квадратичної функції є парабола з вертикальною віссю симетрії.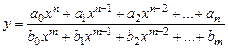 , (2.4)
, (2.4) – сталі.
– сталі. ,
,  та ін.
та ін. називається дробово-лінійною функцією від
називається дробово-лінійною функцією від  , графіком її є гіпербола.
, графіком її є гіпербола. ,
,  і т.д. Окремим випадком алгебраїчної функції є степенева функція
і т.д. Окремим випадком алгебраїчної функції є степенева функція  , де
, де 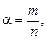
 ,
, 


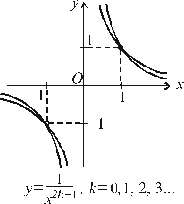
 , де
, де  ,
,  . Функція визначена для всіх значень аргументу
. Функція визначена для всіх значень аргументу  і
і  наведено на рис. 2.7 а, б.
наведено на рис. 2.7 а, б.
 в точці її перетину з віссю Oy дорівнює
в точці її перетину з віссю Oy дорівнює  .
. визначається як функція, обернена до показникової
визначається як функція, обернена до показникової  , для якої введено символ
, для якої введено символ  .
.
 . Графіки функцій
. Графіки функцій 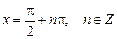 . Множина значень функції
. Множина значень функції  . Графік цієї функції наведено на рис. 2.11.
. Графік цієї функції наведено на рис. 2.11. , де
, де  . Множина значень функції:
. Множина значень функції: 


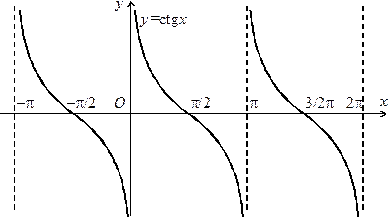
 ,
, 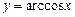 ,
,  ,
,  .
. , синус якої дорівнює
, синус якої дорівнює  . Функція визначена на відрізку [–1;1].
. Функція визначена на відрізку [–1;1]. . Графіком цієї функції є синусоїда, віднесена до вісі
. Графіком цієї функції є синусоїда, віднесена до вісі  . На підставі властивостей дуг, що мають однаковий синус, випливає формула:
. На підставі властивостей дуг, що мають однаковий синус, випливає формула:
 .
. , косинус якої дорівнює
, косинус якої дорівнює  .
. . Графіком такої функції є синусоїда, віднесена до осі
. Графіком такої функції є синусоїда, віднесена до осі  вниз.
вниз. .
.
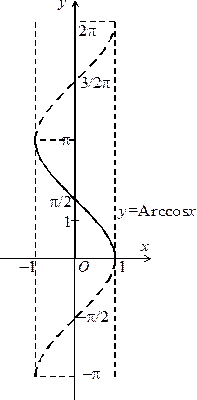
 , тангенс якої дорівнює
, тангенс якої дорівнює  . Функція визначена на всій числовій прямій. Якщо вказати всі значення
. Функція визначена на всій числовій прямій. Якщо вказати всі значення  , причому:
, причому: .
. , котангенс якої дорівнює
, котангенс якої дорівнює  . Функція визначена на всій числовій прямій.
. Функція визначена на всій числовій прямій. , причому:
, причому: .
.




