
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальная система оду. Понятия решения и интегральной кривой. Постановка задачи Коши для Нормальной системы, формулировка тсе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Опред.: Нормальной системой ОДУ называется система ур-ий вида:
Замечание1: Замечание2:Число ур-ий равно числу зависимых переменных Замечание3: Порядок системы равен числу ур-ий Замечание4: Каждое ур-ие ситемы разрешено относительно производной 1-го порядка.Правая часть производных не содержит. Говорят что на промежутке I= Векторная запись системы (1): Опред.: Решение нормальной системы ОДУ (1) назыв-ся упорядоченный набор функций 1) 2) 3) Опред.: Решение нормальной системы ОДУ (1) назыв-ся вектор-функция 1) 2) 3) Опред.: Пусть
Постановка задачи Коши Дано: 1)Система (1) 2) Точка Найти:
Запись:
Теорема(ТСЕ1 для нормальной системы ОДУ): Пусть вектор-функция Тогда существует Нормальная система ЛДУ. Скалярная и матричная запись. Формулировка ТСЕ решения задачи Коши для системы ЛДУ. Нормальную систему порядка n дифференциальных уравнений вида {dy1/dx=a11(x)y1+… a1n(x)yn+b1(x); …; dyn/dx=an1(x)y1+… ann(x)yn+bn(x) (1). называют линейной системой, здесь функции aij(x) и bi(x) определены и непрерывны на I=<a,b>. dyi/dx=j=1Snaij(x)yj+bi(x), 1£ i £n. fi(x, y)= j=1Snaij(x)yj+bi(x), "i,j dfi(x, y)/dyi=aij(x)ÎC(I). Функции fi(x, y) и dfi(x, y)/dyi определены и непрерывны G={xÎI=<a,b>; -¥<y1<¥;…;-¥<yn<¥}=I* R n. Задача Коши для линейной системы: начальные условия: x0ÎI, y10…yn0 – произвольные числа, т.е. y 0Î R n (произвольный вектор). Запишем систему (1) в матричном виде: b (x)=(b1(x)…bn(x))T, A(x) – матрица-функция порядка n. A(x)=||aij||n*n; d y /dx=A(x) y + b (x). A(x), b (x)ÎC(I). Определение. Если b (x)¹ 0, то система d y /dx=A(x) y + b (x) (2) называется неоднородной. Если столбец b (x)= 0, то система ЛДУ называется однородной и имеет вид d y /dx=A(x) y Th.(ТСЕ для системы ЛДУ). Пусть вектор-функция b (x) и матрица-функция A(x) определены и непрерывны на I=<a,b>, x0ÎI, y10…yn0 – произвольные действительные числа. Тогда задача Коши: d y /dx=A(x) y + b (x), y (x0)= y 0 (y 0={y10…yn0}) 1. Имеет решение j (x), определенная на всем I. 2. Это решение единственно (т.е. если j (x) и y (x) – решения, удовлетворяющие условию j (x0)= y (x0), то "xÎI: j (x)º y (x)).
|
|||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 1237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.57.239 (0.01 с.) |

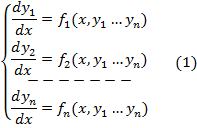
 - зависимые переменные от независимой переменной x
- зависимые переменные от независимой переменной x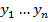
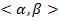 определена вектор-функция
определена вектор-функция 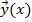 , если на I заданы функции
, если на I заданы функции 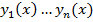

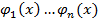 определенных на промежутке I=
определенных на промежутке I= 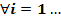 n:
n: 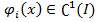
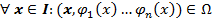

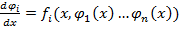
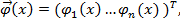 определенная на промежутке I и удовлетворяющая условиям:
определенная на промежутке I и удовлетворяющая условиям: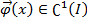
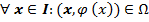
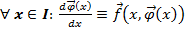
 и заданная параметрически уравнениями:
и заданная параметрически уравнениями: 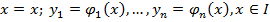 называется интегральной кривой систем (1),(2)
называется интегральной кривой систем (1),(2)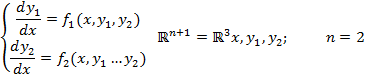

 - решение определенное на окрестности
- решение определенное на окрестности 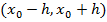 точки
точки 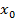 и удовлетворяющая условиям:
и удовлетворяющая условиям: или
или 
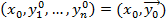 – начальное условие задачи Коши
– начальное условие задачи Коши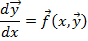

 определены и непрерывны в области
определены и непрерывны в области 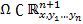 и точка
и точка 
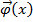 - решение задачи, Коши такое:
- решение задачи, Коши такое: 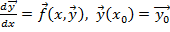 , определенное на интервале
, определенное на интервале 



