
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фср однородной системы лду с постоянными коэффициентами с случае простых действительных корней характеристического уравнения.
Система ЛДУ с постоянными коэффициентами
A=||aij||n×n i,j=1,…n, aij bk (x)
Все решения системы (3) определены на всей числовой прямой, можно доказать, что все решения бесконечно дифференцируемы. Будем искать решения: y(x)= γ Теор 13. Пусть матрица A = ||aij||n´n (aij Î C) имеет n различных собственных значений (хар чисел) l1…ln,тогда век.-функ. y 1= γ 1*el1x … y n= γ n*elnx – где γ k собств вектора, соотв. соб. знач. lk (k=1,..n), образует ФСР сист. (3) и общее реш имеет вид y =C1 γ el1x +…+ Cn γ nelnx, где C1 … Cn – произв числа.
31. ФСР однородной системы ЛДУ с постоянными коэффициентами в случае, когда характеристическое уравнение имеет простые комплексные или кратные действительные корни. Система ЛДУ с постоянными коэффициентами
A=||aij||n×n i,j=1,…n, aij bk (x)
Все решения системы (3) определены на всей числовой прямой, можно доказать, что все решения бесконечно дифференцируемы. Будем искать решения: y(x)= Теорема(1): для того чтобы вектор-функция y=γeλx являлась решением системы Док-во: y=γeλx – реш.сист. <=>
λγeλx=(Aγ)eλx<=>λγ=Aγ<=>Aγ=λγ следовательно согласно определению собственного вектора γ- собственный вектор матрицы А, соответствующий собственному значению λ матрицы А. 1)Пусть среди λ1, … λn встречаются комплексные числа. λ=α+β α,β - действительные числа λ- собственное значение, обозначается:γ≠θ – соответствующий собственный вектор. y=γeλx по теореме 1 – решение системы (5) Теор. 2.: Пусть lÎС и `l комплексно-сопряж. Если y=γeλx, где γЄ Cn явл-ся реш-ем с-мы(3), то ф-я `y(x) также явл-ся реш-ем с-мы (3). При этом, если y(x)=U(x)+iV(x), где U(x), V(x) действит вектор-ф-ции, то U(x) и V(x) также реш-е с-мы (3). Док-во:` y=` γ` eλx =` γ e`λx; согласно теор 1 явл-ся реш (3) т и т т когда λ явл-ся собст значением матр А а γ¹`0 соб вектор удовлет соб знач-ю λ, т е А γ= λ γ; `А` γ=` λ` γ; значит А γ=` λ `γ т е `λ – собст значение матр А, `γ-собст вектор приним собст знач `λ. По теор 1 в этом случае `y= γ e`λx явл решением сист (3)
Предст y(x)=U(x)+iV(x), где U(x) и V(x) действит вект ф-ия. По теор 3, если y(x) явл-ся реш сист (3), то U(x)=Rey(x) и v(x)=Jmy также реш с-мы (3) Лемма: Если y1(x), Док-во: y1(x),…yn(x) – ФСР, то W(0)=0, W(o)=W(U(x)+iV(x),U(x)-iV(x),y3(x),…yn(x))|x=0= =-2iW(U(x),V(x),y3(x),…yn(x))|x=0 ≠ 0, т.к W(0)=0,то W(U(x),V(x),y3(x),…yn(x))|x=0≠0 U(x),V(x),y3(x),…yn(x) –лин. незав. реш.(ФСР) 2) Кратные корни
λ1=λ2=…=λm=μ – корень кратности m характеристического уравнения системы (4) Теорема: пусть μ- корень кратности m характеристического уравнения системы (4), тогда система (5) имеет m линейно независимых решений вида: y=(γ0+γ1t+…+γm-1tm-1)eμx, где γ0,γ1,γm-1
|
|||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.221.204 (0.006 с.) |
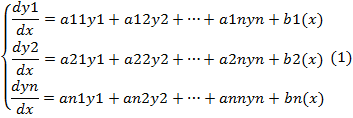
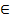 R(C)
R(C) =A y +b(x) (2)
=A y +b(x) (2)  e^(
e^(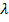 x) (4), где λ
x) (4), где λ 

 R(C)
R(C) =Ay+b(x) (2)
=Ay+b(x) (2)  e^(
e^( x) (4), где λ
x) (4), где λ 
 γeλx
γeλx 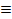 A(γeλx)
A(γeλx)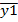 (x), y3(x),…, yn(x) - ФСР системы(5) и y1(x)=U(x)+iV(x), а
(x), y3(x),…, yn(x) - ФСР системы(5) и y1(x)=U(x)+iV(x), а  =Ay (3) A=||aij||n×n aij
=Ay (3) A=||aij||n×n aij 


