
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ОДУ первого порядка, разрешенные относительно производной. Понятия решения и интегральной кривой уравнения.Содержание книги
Поиск на нашем сайте Постановка задачи Коши. Пусть область D∈ Определение 3. φ(x) определена на промежутке I=<α,β> называют решением уравнения y'=F(x,y) если: 1) φ(x) ∈C1(I) 2) ∀x∈I:(x, φ(x)) 3) ∀x∈I:φ'(x) ≡F(x, φ(x)) Определение 4. Если y= φ(x) является решением y'=F(x,y),то график этой функции называют интегральной кривой уравнения y'=F(x,y).Ясно,что интегральная кривая ∈ D Геометрическая интерпретация Говорят,что в области D∈R2 задано векторное поле Для уравнения y'=F(x,y) построено векторное поле
Пусть y= φ(x) интегральная кривая y'=F(x,y), В точке (x, y) y'= φ' (x)=F(x, φ(x))=F(x,y) Т.е тангенс угла наклона к φ= φ(x) равен F(x,y) Постановка Задачи Коши Постановка задачи –необходимо понять,что задано и что надо найти Дано: В области D заданы дифф.ур-ия y'= F(x,y) и два числа x0 и y0 такие,что (x0,y0) ∈D Найти: решение y= φ(x) уравнения y'=F(x,y) определена на некотором интервале где x0∈ I=<α,β> и удовлетворяет условию φ(x0)=y0, числа x0 и y0 называются начальными условиями. Условная запись задачи Коши y'= F(x,y),y(x0)=y0 Замечания 1) Если F(x,y) ∈C(D) То задача Коши имеет решение в любой точке в области D 2) Решений у уравнения y'= F(x,y)бесконечно много 3) (x0,y0) ∈D:Для единственности решения требует дополнительные условия Формулировка теоремы существования и единственности (ТСЕ). Понятие общего решения. Обобщение некоторых понятий.Пусть f(x,y) определена в области D∈ Рассматриваем задачу коши (8) Пусть φ1(x) и φ2(x) решения (8),т.е φ1(x),φ2(x) - решение y'=F(x,y), φ1(x0)=y0 φ2(x0)=y0 Определение 5. Говорят,что задача Коши (8) имеет единственное решение если любые два решения φ1(x) и φ2(x) этой задачи,совпадают на некоторой окрестности точки x0 т.е ∃ δ>0 ∀x∈(x0 – δ, x0 + δ): φ1(x) ≡ φ2(x) ТеоремаТСЕ1(локальная) Пусть на области D∈ 1)Определена на некоторой окрестности (x0 – h, x0 + h) точки x0 , удовлетворяет условию φ(x0 )= y0 2)Такое решение единственное(Без док-ва) Замечание к ТСЕ Пусть в D выполняется условие ТСЕ1 1)В D бесконечно много решений уравнения, x0 - точка (x0 , y0) ∈D.Через эту точку проходит единственное решение y=φ(x0 , y0).Все эти решения не совпадают Определение 6. Пусть Функция y=φ(x,C) называют общем решением y'= F(x,y) в области D,если 1) ∀C: φ(x,C) решением φ(x,C) 2) Любое частное решение y'=F(x,y) может быть получен из φ(x,C) подбором соответствующего значения C 20 Решением задачи может быть определена лишь на некоторой (небольшой) окрестности точки x0 Уравнения с разделяющимися переменными. Однородные уравнения. Примеры. ОДУ вида:(3) Теорема 1.Если Доко-во (3)y (3 Проинтегрируем по x: Обозначим F(x)= G(y)= G(y)=F(x)+C Т.к G Y=G-1(f(x)+C) – решением уравнения (3) Найдем решение проходящие (x0 , y0) G(y0)=F(x0)+C; y= G-1(f(x)) Замечания 1)Если ∃y* такое g(y*)=0 тогда,уравнение (3) имеет решение y=y* 2) Алгоритм решения ур-ия (3) a)g(y)=0 найти y*g(y*)=0,тогда y= y* б)g(y) ≠0; 3) Такое ур-ие сводится к ур-ию с разделяющими переменными x- независимая переменная,z=z(x) z'=a+bf(2) уравнение с раздел. Перемен z=ax+by+c и z'=a+by' Пример: ydx = (x +1) dy Однородные уравнения (4)y'=F( Уравнение вида (4) называют однородным, x – независимая переменная U=U(x) y=ux;u= Уравнение (4) преобразуют к виду:u'x+u=F(u); u'= Пример: xy'=y-x
|
||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.011 с.) |

 и F(x,y) определена на D y'=F(x,y)
и F(x,y) определена на D y'=F(x,y) ,если в каждой точке M(x,y) ∈ В поставлен в соответствии вектор
,если в каждой точке M(x,y) ∈ В поставлен в соответствии вектор  – поле направления
– поле направления
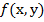 и
и  (x,y) определена и непрерывна и точка (x0,y0) ∈D.Тогда уравнение
(x,y) определена и непрерывна и точка (x0,y0) ∈D.Тогда уравнение  имеет решение φ(x)
имеет решение φ(x) –называют уравнение с разделяющимися переменными
–называют уравнение с разделяющимися переменными непрерывная при a<x<b,
непрерывная при a<x<b,  непрерывна при c<y<d, причем ∀y∈(c,d):g(y)≠0,то через каждую точку M0(x0 , y0) прямоугольника D=
непрерывна при c<y<d, причем ∀y∈(c,d):g(y)≠0,то через каждую точку M0(x0 , y0) прямоугольника D=  проходит единственное решение уравнения (3)
проходит единственное решение уравнения (3) =f(x)g(y);g(y) ≠0
=f(x)g(y);g(y) ≠0 =f(x)
=f(x) =
=  ó
ó 

 из (3*)
из (3*) ≠0,то у G(y) существует обратный G-1
≠0,то у G(y) существует обратный G-1 =f(x)ó
=f(x)ó 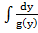 =
=  =f(ax+by+c),a,b,c∈ ℝ, b≠0
=f(ax+by+c),a,b,c∈ ℝ, b≠0
 ; y'=u'x+u
; y'=u'x+u




