Лабораторная работа №1. Решение простейших задач обработки матриц в системе MATLAB

ВВЕДЕНИЕ В MATLAB

Лабораторный практикум

 

Учебное пособие по курсу «Информатика»

для студентов всех направлений МЭИ

 

 

Москва Издательство МЭИ 2006

 

УДК

621.398

Б28

Утверждено учебным управлением МЭИ в качестве учебного пособия для студентов

Подготовлено на кафедре прикладной математики
Рецензенты:

доктор техн. наук, профессор В.П. Будак (МЭИ),

доцент Е.С. Перевезенцева (кафедра прикладной информатики Московского психологического университета)

 

Батасова В.С.

Введение в MATLAB. Лабораторный практикум. Учебное пособие по курсу «Информатика».. – М.: Издательство МЭИ, 2006.–52 с.

Практикум предназначен для овладения основами работы в интерактивной среде MATLAB с целью применения при изучении специальных дисциплин и в практической деятельности. Практикум охватывает следующие темы: работа в командном окне, функции и скрипты, графический вывод, манипуляторы функций, создание оконных приложений. Каждая работа состоит из теоретического введения и задания.

Лабораторный практикум предназначен для студентов младших курсов всех специальностей МЭИ при изучении информатики.

 

 

Учебное издание

Батасова Валентина Сергеевна

Введение в MATLAB. Лабораторный практикум

Учебное пособие по курсу «Информатика»

Редактор

ЛР № от

 

Издательство МЭИ, 11250, Москва, Красноказарменная, д. 14

 

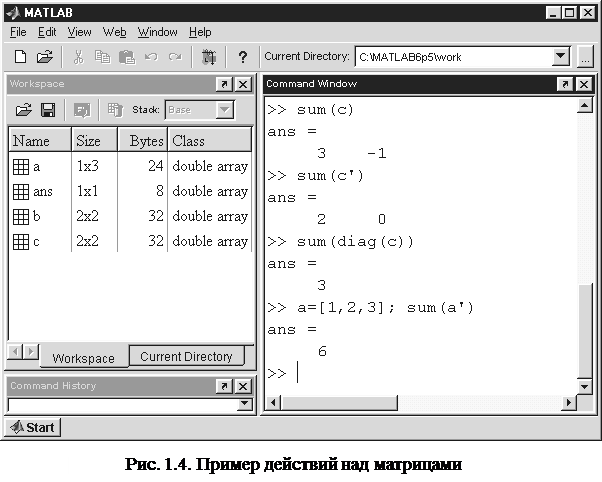
ISBN © Московский энергетический институт, 2006

Введение

MATLAB – одна из самых популярных интерактивных систем для инже­нерных и научных расчетов. MATLAB - это одновременно пакет прикладных программ и используемый в этом пакете язык программирования. Система MATLAB разрабатывается фирмой The MathWorks, основанной в 1984 г.

Особенность языка MATLAB состоит в том, что основным элементом данных является матрица. Это позволяет решать задачи, в которых использу­ются матрицы и вектора, в несколько раз быстрее, чем при использовании «скалярных» языков программирования, таких как Си, Фортран, Паскаль. На­звание MATLAB означает «матричная лаборатория» (сокращение от «Matrix Laboratory»). Скаляры в MATLAB обрабатываются как матрицы размера 1*1.

MATLAB работает под управлением большинства современных опера­ционных систем, в том числе Windows, Mac OS, Linux и Unix. Основные об­ласти применения MATLAB: численные методы, моде­лирование, сбор и анализ данных, инженерная и научная графика, разработка программ, включая создание графического интерфейса. В состав MATLAB входят специализированные группы программ (toolboxes), предназначенные для решения частных классов задач (обработки сигналов, нейронных сетей, и т. д.).

Пособие было подготовлено для студентов факультета Электронной тех­ники и прошло апробацию на этом факультете в рамках дисциплины «Инфор­матика». Оно может быть использовано для всех инженерных специальностей. Цель практикума – приобретение студентами навыков работы в среде MATLAB для дальнейшего применения их в специаль­ных дисциплинах и практической деятельности Небольшой объем часов, отведенных на информатику, и обширный набор тем, подлежащих рассмотрению в этой дисциплине, застав­ляют ограничиться вводным курсом из пяти лабораторных работ. При написа­нии пособия использовались источники [1,2].

Для успешной работы с пособием от студентов требуется умение работать в операционной среде Windows на пользовательском уровне и знание основ программирования на Паскале.

Автор выражает искреннюю благодарность инициатору написания этого пособия профессору кафедры Светотехники МЭИ В.П. Будаку за своевремен­ное и доброжелательное обсуждение работы, а также преподавателям кафедры прикладной математики: П.В. Гречкиной, Э.С. Комаровой, В.И. Луканиной, К.Г. Меньшиковой, А.А. Незнанову, С.В. Смагину, - принимавшим участие в апробации пособия на факультете Электронной техники.

Теоретическая часть

Работа с файлами

Существует возможность вводить матрицы из текстового файла, сфор­мированного вне среды MATLAB. В текстовом файле матрица должна быть представлена как прямоугольная таблица чисел, разделенных пробелами, с равным количеством элементов в каждой строке. Имя файла должно иметь не­пустое расширение, отличное от.mat. Команда

load имя_файла.расширение

прочитает этот файл в переменную имя_файла. Например, из файла m.txt данные будут считаны в переменную m. По умолчанию файл находится в те­кущей директории среды MATLAB; для изменения директории перед именем файла надо указать путь к нему; например:

load d:\student\m.txt

Для сохранения массива в текстовый файл можно воспользоваться командой:

save [ путь к файлу\ ] имя_файла.расширение имя массива -ASCII

Путь к файлу заключен в квадратные скобки как необязательный элемент ко­манды. Расширение может быть любым, кроме.mat. Команда

save a.txt a -ASCII

сохранит массив а в файле a.txt текущей директории.

Команды load и save имеют другие режимы использования. Кроме того, в MATLAB существуют другие команды чтения данных из файла и сохранения их в файл. Эти возможности, к сожалению, выходят за рамки нашего курса.

Оператор двоеточия

Оператор двоеточия (:) – один из наиболее часто используемых операто­ров MATLAB. Его вид:

начальное значение: шаг: конечное значение

Оператор предполагает изменение от начального значения до конечного с заданным шагом. Шаг с предшествующим двоеточием может быть опущен, тогда по правилу умолчания шаг равен 1.

Оператор двоеточия входит в состав оператора параметрического цикла for. Он также может использоваться самостоятельно для задания значений эле­ментам массивов или для работы с частью массива. Примеры использования оператора двоеточия представлены на рис. 1.5.

 

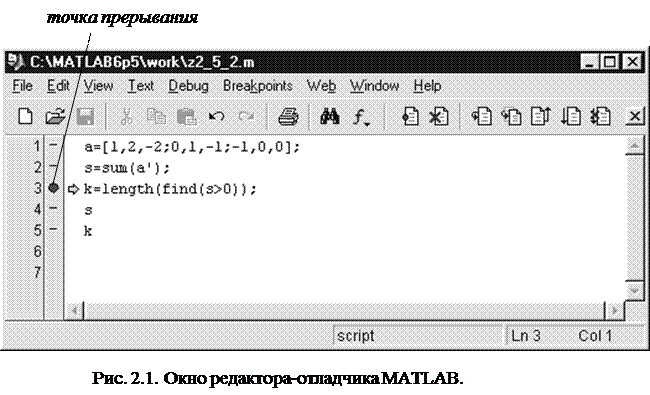
Теоретическая часть

М-файлы

М-файл – это текстовый файл, содержащий инструкции языка MATLAB, с расширением.m. Для вызова М-файла достаточно записать в окне команд MATLAB (или в другом М-файле) его имя без расширения.

Создать М-файл можно в любом текстовом редакторе, но предпочти­тельней использовать встроенный редактор MATLAB. Чтобы его вызвать, надо воспользоваться пунктом File главного меню MATLAB; например, для созда­ния File /New/M-file. Для открытия существующего М-файла также можно вве­сти команду: edit имя_файла (без расширения). Для закрытия М-файла надо воспользоваться командой главного меню окна редактора File/Save имя_файла. Существует два вида М-файлов: скрипты и функции. Их мы рассмотрим в сле­дующих параграфах.

Скрипты

Скрипты – это простейшие М-файлы. Они имеют с командным окном (или с вызвавшим скрипт М-файлом) общее рабочее пространство переменных. При вызове скрипта просто выполняются содержащиеся в нем команды. Например, создадим текстовый файл z2_5_2.m, содержащий команды

s=sum(a');

k=length(find(s>0));

Тогда из командного окна с помощью инструкции

>> z2_5_2

мы вычислим число строк матрицы а с положительной суммой элементов.

Функции

Функции – это подпрограммы языка MATLAB. Общий вид функции:

function [ СписокВыхода ]= ИмяФункции (СписокВхода)

% комментарии

исполняемые операторы

Первая строка, начинающаяся с ключевого слова functionявляется заго­ловком функции. СписокВхода и СписокВыхода – это списки входных и вы­ходных формальных параметров; элементы списков перечисляются через запя­тую. В отличие от Паскаля, функция MATLAB может иметь несколько выход­ных значений, и поэтому нет необходимости в процедурах общего назначения. Если выходной параметр один, то его можно не заключать в квадратные скобки.

После заголовка идут строки комментариев. Как во всех алгоритмиче­ских языках, комментарии не обрабатываются транслятором, а используются для пояснения программы. В языке MATLAB комментарием считается текст от символа % до конца строки. Комментарии, которые стоят между заголовком функции MATLAB и первой пустой или исполняемой строкой, выводятся как информационный текст при вызове команды
help ИмяФункции

Исполняемые операторызаписываются как обычно при кодировании алгоритма.

Текст функции хранится в М-файле, причем имя файла (без расширения) должно совпадать с именем функции. Функция имеет собственное рабочее пространство переменных, независимое от пространства рабочего окна или вы­звавшего функцию М-файла (базового пространства или базовой рабочей об­ласти).

Вызов функции осуществляется инструкцией:

[ СписокВыхода ]= ИмяФункции (СписокВхода),

в которой участвуют списки фактических параметров, т. е. переменных базовой рабочей области.

Пример 2. Функция sumk определяет сумму каждой строки произволь­ной матрицы а и число ее строк с положительной суммой:

function [s,k]=sumk(a)

% s-sums of rows, k- number of positive sums

s=sum(a');% calculate sums

k=length(find(s>0));%calculate number of positive sums

Текст функции должен быть сохранен в файле sumk.m.

Тогда операторы, набранные в командном окне:

[sa,ka]=sumk(a);

[sb,kb]=sumk(b);

обеспечат вычисление sa (sb) – массива сумм строк матрицы a (b), и ka (kb) числа положительных значений среди этих сумм.

Глобальные переменные

Память функции отделена от рабочей области, из которой вызывается функция (базовой рабочей области). При обращении к функции осуществля­ется копирование данных из базовой рабочей области в рабочую область функции. Студенты, знающие Паскаль, должны ответить на вопрос: какие пе­ременные передаются по ссылке, а какие по значению? При необходимости использования функцией данных базовой рабочей области без пересылок данных следует воспользоваться описателем global. Глобальные переменные должны объявляться как в функции, так и в базовой рабочей области. Чтобы отличать их от других переменных, принято именовать их большими буквами, но это правило не является обязательным.

Пример 3. Функция

function h=falling(t)

global GRAVITY

h=1/2*GRAVITY*t.^2;

может быть вызвана следующими командами:

global GRAVITY

GRAVITY=9.8;

y=falling(0.1:0.1:1);

Ответьте на вопрос: в каких ситуациях оправдано использование глобальных переменных?

Для удаления глобальной переменной из рабочей области используется команда clear global имя_переменной.

Отладка М-файлов

Встроенный редактор М-файлов является также и отладчиком (Editor/Debugger). Приемы отладки такие же, как в Паскале. Рассмотрим минимальный набор средств отладки.

Установка (снятие) точек прерывания осуществляется следующими способами:

· щелчком на полосе точек отладки (см. рис. 2.1) возле оператора, на котором необходимо сделать прерывание;

· командой Breakpoints/Set (Clear) Breakpoints (курсор должен стоять на нужном операторе);

· клавишей F12;

· кнопками панели инструментов.

Активные точки отладки имеют красный цвет, неактивные серый. Причиной неактивности точек отладки может быть наличие синтаксических ошибок в М-файле или несохранение последней версии файла.

Трассировка М-файла может осуществляться с помощью пункта глав­ного меню Debug, указанных в этом пункте функциональных клавиш или кно­пок панели инструментов. Возможности трассировки:

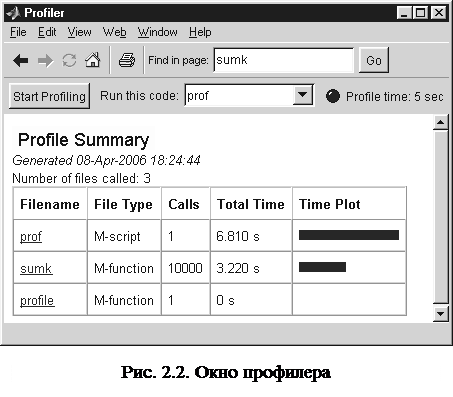
Step – пооператорное выполнение М-файла, вызов функции считается одним оператором (аналогично Trace в Delphi);

Step In – пооператорное выполнение М-файла c заходом в функции (аналогично Trace Into в Delphi);

Step Out – после захода в функцию выполнение ее до конца и после выхода из функции пауза;

Continue – выполнение М-файла до его конца или до следующей точки прерывания.

Просмотр значений переменных во время паузы может осуществляться следующими способами:

· установкой курсора слева от переменной в окне редактора/отладчика, при этом на несколько секунд появится небольшой прямоугольник с ее текущим значением;

· оцениванием выделенного выражения; после выделения вызвать контекстное меню или выбрать пункт Evaluate Selection;

· использованием редактора массивов рабочей области функции; для входа в редактор сделать щелчок мышью на пиктограмме интересующей переменной в рабочей области функции; нужная рабочая область выбирается из раскрывающегося списка Stack;

· просмотром значения в командном окне; в процессе отладки приглашение в командном окне изменит свой вид с «>>» на «K>>»; после приглашения достаточно ввести имя переменной и нажать Enter.

Профилирование М-файлов

Профилирование (profiling) программного кода – это измерение времени выполнения подпрограмм и скриптов, вызываемых из этого кода. Профилирование необ­ходимо для выяснения причин медленной работы программы и является мощным средством оптимизации про­грамм. MATLAB имеет специальный инструмент профилирования – про­филер.

Окно профилера (см. рис. 2.2) вызывается с помощью команды главного меню View/Profiler. В поле Run this code записывается команда вызова профилируемого М-файла. Нажатие кнопки Start Profiling запускает процесс про­филирования. Индикатор Profile time показывает время профилирования; его исходный цвет черный, во время профилирования меняется на зе­леный. После завершения профилирования его итоги выводятся в окне профилера. На рис. 2.2 представлен результат профилирования М-файла prof, в котором в цикле 10000 раз вызывается функция sumk (см. п. 1.3):

b=[-8,7;7,7];

for i=1:10000

[sb,kb]=sumk(b);

end

Ниже дан перевод итогов профилирования. Последний столбец итоговой таблицы содержит диаграмму общего времени выполнения функций.

 

2. Задание

1. Сделайте скрипт для алгоритма задачи [3] 2.5.2.N+1. Ввод исходных дан­ных и вывод результатов не включайте в скрипт. Вызовите скрипт не­сколько раз из окна команд для обработки матрицы, значения которой за­давайте двумя способами: присваиванием и вводом из файла.

2. Оформите алгоритм задачи [3] 2.5.2.N+1 как функцию MATLAB. Вызовите эту функцию несколько из окна команд для обработки матриц с различ­ными именами.

3. Выполните в среде MATLAB задачу [3] 4.2.6.N+1.

4. Для отладки каждого М-файла организуйте его пооператорное выполне­ние, в ходе которого проанализируйте, правильно ли изменяются значения переменных.

5. Выполните профилирование разработанных М-файлов. Чтобы время выполнения было значимым, организуйте многократный вызов М-файла в цикле по образцу п.1.6.

Теоретическая часть

Окна изображения

Первое обращение к функции plot открывает окно изображения (с заго­ловком Figure №1). При дальнейших вызовах plot рисует новые графики в уже имеющемся окне, при этом предыдущие графики стираются. Если перед обра­щением к plot вызвать команду hold on, новые графики будут добавляться к имеющимся. При необходимости добавление графика сопровождается автома­тическим изменением масштаба. Следующая последовательность команд на­глядно иллюстрирует действие команды hold on (см. рис.3.4):

hold on

y=(x.^2)./10; plot(x,y,'k-');

legend('sin(x)','sin(x-0.25)','sin(x-0.5)','0.1*x^2',2);

Для открытия нового окна изображения достаточно набрать команду figure без параметров. Выполнение команды figure(n) приведет активизации существующего окна с номером n. Последующие графики будут выводиться в это окно. Номер окна изображения показан в его заголовке.

Сохранение графика

Команда главного меню File/Save (Save as) сохраняет график в MATLAB-формате. Команда File/Export from осуществляет сохранение в других графиче­ских форматах (TIFF, BMP, и т. п.). Можно также использовать оператор ко­мандной строки:

saveas(gcf,' [ путь \] имя.расширение')

где gcf –цифровой идентификатор файла (Handle) текущего графического окна; если путь не указан, то файл сохраняется в текущей дирек­тории MATLAB.

Задание

1. Запустите MATLAB и выполните все примеры теоретической части.

2. Запрограммируйте функции заданий [3] 1.7.N,N+1. Предварительно скорректируйте значения функции в особых точках с помощью оператора if или прибавления к нулевым значениям eps. Учтите, что в ситуациях, где среды Borland Pascal и DELPHI выдают сообщение об ошибке (извлечение корня из отрицательного числа, взятие логарифма отрицательного числа, и т. п.), MATLAB вычисляет комплексное значение функции. Постройте графики для функций из заданий [3] 1.7.N,N+1. Визуально определите точки, в которых функции принимают минимальное, максимальное и нулевое значение.

3. Постройте график функции задания [3] 1.8.N+1 и визуально определите характерную точку функции в соответствии с заданием.

4. С помощью функции mesh постройте изображение поверхности для функции двух переменных из задания [3] 2.1.N+1.

5. Расположите все графики в одном окне, используя функцию subplot.

6. Сохраните все графики в формате MATLAB и в формате BMP.

 

 

Теоретическая часть

Класс Function Functions

Функции этого класса работают с нелинейными функциями скалярного аргумента как с подпрограммами-параметрами. предназначен для решения следующих задач:

· нахождение нулей функций (решение уравнений);

· оптимизация;

· вычисление определенных интегралов;

· обыкновенные дифференциальные уравнения.

Рассмотрим некоторые функции класса:

fminsearch(манипулятор_функции, начальное_приближение) вычисляет точку локального минимума функции;

fzero(манипулятор_функции, начальное_приближение) вычисляет точку ло­кальный нуль функции;

quad(манипулятор_функции, нижняя_граница, верхняя_граница) вычисляет определенный интеграл по методу Симпсона, quadl вычисляет определенный интеграл по методу Лобатто.

Пример 2. Рассмотрим функцию:

function y = humps(x)

y = 1./((x-.3).^2 +.01) + 1./((x-.9).^2 +.04) - 6;

График функции приведен на рис. 4.1. Результаты ее исследования с помощью выше перечисленных функций даны на рис. 4.2.

1.4.

Пример использования глобальных переменных

Пусть исследуемая нелинейная функция скалярного аргумента известна с точностью до параметра. Например, требуется с помощью функции с найти (относительно x) корень уравнения:

x-p cosx=0 (1)

Так как fzero может применяться только к функциям одного аргумента, параметр р необходимо передавать как глобальную переменную. Функция f, описывающая левую часть уравнения, имеет вид:

function y=f(x)

% p-глобальная переменная

global p

y=x-p.*cos(x);

Вычисление корня уравнения (1) для значений р, изменяющихся от 0.3 до 0.6 с шагом 0.1, осуществляется с помощью команд:

global p

i=1;

for p=0.3:0.1:0.6

z(i)=fzero(@f,0.5); i=i+1;

end

Задание

1. Для функций заданий [3] 1.7.N,N+1, [3] 1.8.N+1 с помощью методов класса Function Functions определить характерные точки. Результаты решения сравнить с полученными в лабораторной работе №3.

2. На языке MATLAB разработать подпрограмму решения уравнения методом деления отрезка пополам, вид уравнения задать с помощью манипулятора функции. Используя подпрограмму, решить два уравнения: [3] 1.7.N,N+1. Результаты решения сравнить с п.1 задания.

3. Включить в функцию F(x) задания [3] 1.7.N параметр р. Задавая значение р в командном окне MATLAB и передавая его F(x) как глобальную переменную, найти корень уравнения F(x)=0 для нескольких значений p.

Теоретическая часть

Создание меню

Построение меню осуществляется с помощью редактора, который можно вызвать кнопкой панели инструментов редактора интерфейса (см. рис.5.2). Окно редактора меню имеет две вкладки, соответственно, для создания глав­ного меню (Menu Bar) и контекстного меню (Context Menu). Читатель должен знать, что такое главное и контекстное меню.

Рассмотрим правила создания контекстного меню на примере программы п. 1.3. Открыв заготовку приложения, вызовем редактор меню и перейдем на вкладку контекстного меню (см. рис. 5.8). Добавить меню можно с помощью кнопки панели инструментов. Можно сделать несколько контекстных меню и каждое из них связать с некоторым элементом приложения. В нашем примере будет одно меню, свойству Tag которого дадим значение context_menu. Подключим меню к окну приложения, задав (выбором из списка) свойству окна UIContextMenu значение тэга меню (в нашем случае context_menu).

Добавим в меню (с помощью соответствующей кнопки – см. рис. 5.8) три пункта, дублирующие кнопки Push Button приложения. Свойство Label пунктов – это их название, видимое пользователем при вызове меню. Установим свойству Label пунктов меню значения конкатенация, сложение и выход, соответственно.

Для каждого пункта меню можно создать обработчик и скопировать в него тело обработчика соответствующей компоненты Push Button. Однако предпочтительней подключить имеющийся обработчик, скопировав значение свойства Callback компоненты Push Button в свойство Callback пункта меню. После такого копирования можно запустить приложение и попробовать, как работает контекстное меню.

Главное меню создается аналогично контекстному. Отличие состоит в том, что главное меню не надо подключать к конкретной визуальной компоненте: оно всегда принадлежит окну приложения.

 

Пример приложения с выводом графика

Для вывода графика предназначена компонента Axes. Добавим эту компоненту на заготовку окна приложения и с помощью мыши установим ее размеры (см. рис. 5.9). Сделаем так, чтобы в этой области рисовались графики разных функций. Например, при нажатии одной кнопки выводился график sin(x), а при нажатии другой – cos(x). Поставим на заготовку два объекта Push Button; их свойство String установим в значения sin и cos, соответственно.

Для выбора диапазона значений аргумента х будем использовать компо­ненту Popup Menu. В DELPHI так называется компонента для контекстного меню. В MATLAB это совершенно другая компонента, аналог ComboBox DELPHI. Ее назначение – выбор одной из строк раскрывающегося списка. В свойство String запишем две строки: «от 0 до 2 пи» и «от 0 до 10 пи». Со­храним приложение под именем PrimerGraphic.

Чтобы массивы значений х не вычислять многократно, запишем операторы вычисления х в тело открывающей функции приложения. Эта функция работает один раз при запуске приложения до момента, когда компоненты окна становятся видимыми. В ней программируются действия, которые должны быть выполнены до активизации всех элементов окна приложения. Имя функции образуется из значения свойства Name окна приложения и символов _OpeningFcn. Чтобы переменные, получившие значения при работе открывающей функции, были доступны в других функциях приложения, их следует сделать полями структуры handles. В тело открывающей функции вставим операторы:

handles.x2pi = 0:pi/10:2*pi; % значения х из интервала от 0 до 2 пи

handles.x10pi = 0:pi/10:10*pi; % значения х из интервала от 0 до 10 пи

handles.current_data=handles.x2pi; % поле current_data структуры handles

% хранит текущиеся значения.х, используемые при выводе графиков

y=sin(handles.x2pi); % при запуске окна приложения в нем рисуется

plot(handles.x2pi,y); % график функции sin(x), 0<=x<=2пи

Эти операторы должны располагаться до двух автоматически генерируемых операторов:

handles.output = hObject

guidata(hObject, handles)

Назначение первого оператора рассматривать не будем. Второй оператор обеспечивает сохранение структуры handles.

Компонента Popup Menu должна обеспечивать выбор одного из двух массивов значений х. В обработчик компоненты запишем программный код:

val = get(hObject,'Value'); % свойство Value объекта Popup Menu хранит

% номер выбранной строки, его значение присваивается переменной val

str = get(hObject, 'String'); % переменной str присваивается

% значение свойства String

switch str{val}; % переключатель записывает в handles.current_data

% выбранные значения х

case 'от 0 до 2 пи' % Пользователь выбрал значения х от 0 до 2 пи

handles.current_data = handles.x2pi;

case 'от 0 до 10 пи' % Пользователь выбрал значения х от 0 до 10 пи

handles.current_data = handles.x10pi;

end

В обработчик кнопки вывода графика синуса запишем операторы:

y=sin(handles.current_data);

plot(handles.current_data,y);

Аналогичные операторы запишем для вывода графика косинуса. Приложение готово.

Задание

1. Выполнить все примеры теоретической части.

2. Разработать оконное приложение для решения задачи [5] 2.N+1.

3. По образцу п. 1.5 создать приложение, выводящее графики функций из задач [3] 1.7.N, N+1, 1.8.N+1 для различных интервалов значений аргумента.

Приложение. Описание алгоритмического языка MATLAB

Изучая алгоритмический язык ПАСКАЛЬ, мы придерживались точки зрения, что главное в программировании - это анализ задачи, выбор структур данных и разработка алгоритма. Кодирование на алгоритмическом языке является трудоемкой рутинной работой, но не содержит принципиальных трудностей. Выбор языка программирования (среди языков, ориентированных на решение определенного класса задач) не имеет решающего значения. Различия в пра­вилах построения фраз языка не являются принципиальными, освое­ние этих правил - дело практики, а приверженность программиста к ка­кому-то алгоритмическому языку обычно является следствием мно­голетней привычки. Используя этот подход, мы будем изучать язык программирования MATLAB, учитывая, что Вы умеете программировать на ПАСКАЛЕ.

П.1. Имена в MATLAB

Имя представляет последовательность латинских букв, цифр и символов подчеркивания, на первом месте которой стоит буква. Большие и малые буквы образуют различные имена. Имена могут состоять из произвольного числа символов, но различаются по первым символам, число которых возвращает функция namelengthmax. Вызовите ее из окна команд и узнайте это число.

Переменные, как правило, не объявляются. Тип и размер переменных определя­ются присваиваемыми значениями и могут из­меняться в процессе выполнения программы. В таблице П.1 приведены некоторые функции, возвращаю­щие специальные величины, которые могут быть полезны при работе в MATLAB. Эти имена (в том числе i и j) не стоит использовать для других це­лей.

 

 

Таблица П.1. Специальные величины и некоторые функции

Функция	Возвращаемое значение
ans	самый последний результат (переменная). Если вы не присвоили значение выражения какой-нибудь переменной, то MATLAB автоматически сохранит результат в ans
eps	Относительная погрешность при вычислениях с плавающей точкой
realmax	Максимальное вещественное значение
realmin	Минимальное вещественное значение
pi	3.1415926535897...
i, j	Мнимая единица
inf	Бесконечность – результат деления n/0, если n не является комплексным числом и n¹0
NaN	Not-a-Number – не число. В том числе выражения вида 0/0, inf/inf и n/0 при комплексном n.
version	версия MATLAB
abs(x)	абсолютная величина x
atan(x)	arctg(x)
exp(x)	e^x
log(x)	натуральный логарифм x
sin(x)	sin(x)
cos(x)	cos(x)
tan(x)	tg(x)

П.2. Типы данных

MATLAB имеет 15 основных типов данных. Каждый тип явля­ется массивом. Основные типы показаны жирным шрифтом на диаграмме рис. П.1.

Целые типы могут быть знаковыми или беззнаковыми, название беззнаковых типов начинается с латинской буквы u (от unsigned - англ. беззнаковый). Целое число, на которое оканчивается название типа, показывает, сколько байтов занимает одно значение этого типа. Естественно, чем большая память отводится на значение, тем шире диапазон его изменения.

MATLAB имеет два вещественных типа – single и double. Тип single характеризуется меньшей точностью представления чисел и меньшим диапазон чисел, чем double; соответственно, значение single занимает меньше памяти. Данные типа double имеют точность приблизительно 16 значащих десятичных цифр и диапазон изменения приблизительно от 10^-308 до 10⁺³⁰⁸.

Тип double является основным типом MATLAB. Он принимается по умолчанию для числовых переменных. Переход к другим типам (например, int8) иллюстрируется рис. П.2. Все вычисления в MATLAB выполняются над переменными типа double. Остальные числовые типы используются для компактного хранения данных.

Манипуляторы функций (handle) имеют такое же назначение, как и процедуры-параметры ПАСКАЛЯ. Они рассматриваются в лабораторной работе №3.

Тип структура (structure) подобен типу запись в ПАСКАЛЕ. Тип cell не имеет аналога в Паскале; он представляет собой массив, элементом которого является другой массив. Эти два типа, а также два дополнительных типа (классы пользовательские и java) мы рассматривать не будем.

 

П.3. Константы

Правила записи числовых констант поясним на примерах:

3 -99 0.0001 9.6397238 1.60210e-20 6.02252e23

Можно использовать комплексные данные. Мнимая единица может обозначать i или j. Например, 1i -3.14159j 3e5i

Логические константы: 1 - истина (true) и 0 - ложь (false). При проверке условий любое ненулевое значение воспринимается как истина, а нулевое как ложь.

Символьная константа – это последовательность символов, заключенная в апострофы ('Hello!').

П.4. Операции и выражения

Арифметические операции MATLAB представлены в таблице П.2. Имеется два вида арифметических операций. Матричные операции вы­полняются по правилам линейной алгебры. Простые операции над массивами выполняются поэлементно над соответствующими элементами массивов оди­наковых размеров. Для обозначения простой операции перед знаком операции ставится точка. Например,.* обозначает простое умножение. Когда матрич­ная и простая операция выполняются одинаково, предшествующая точка не ставится (существует только операция +, операция.+ не существует)

Простая операция может выполняться над парой скаляр-массив. Тогда скаляр участвует в операции над каждым элементом массива. Такая ситуация называется скалярным расширением. Примеры матричной, простой опера­ции и скалярного расширения представлены на рис. П.3.

Таблица П.2. Арифметические операции MATLAB

Оператор	Описание
+	Сложение
-	Вычитание
.*	Умножение
./	Правое деление: а./в – каждый элемент а делится на соответствующий элемент в
.\	Левое деление: а.\в – каждый элемент в делится на соответствующий элемент а
+	Унарный плюс
-	Унарный минус
:	Операция двоеточия
.^	Возведение в степень
.'	Транспонирование
'	Комплексно-сопряженное транспонирование
*	Матричное умножение
/	Матричное правое деление: а/вºа*в^-1
\	Матричное левое деление: а\вºа^-1*в
^	Матричное возведение в степень

Операции отношения представлены в таблице П.3. Они выполняются над массивами одинакового размера (как простые арифметические операции). В результате получается массив такого же размера; каждый его элемент равен единице, если для соответствующих элементов исходных массивов соотношение выполнено, и нулю в противном случае.

Таблица П.3. Операции отношения

Оператор	Описание	Оператор	Описание
<	Меньше	>	Больше
<=	Меньше или равно	>=	Больше или равно
==	Равно	~=	Не равно

Пример.

A = [2 7 6;9 0 5;3 0.5 6];

B = [8 7 0;3 2 5;4 -1 7];

A == B

ans =

0 1 0

0 0 1

0 0 0

Допустимо скалярное расширение, когда каждый элемент массива сравнивается со скаляром.

Логические операции бывают поэлементные и укороченные. Поэле­ментные логические операции выполняются над массивами одинакового размера. Нулевое значение элемента исходного массива воспринимается как истина, ненулевое – как ложь. Результатом является массив такого же размера из нулей и единиц (0 ставится, если результат сравнения ложь, а 1 – истина). Поэлементные логические операции представлены в таблице П.4. В третьем столбце таблицы П.4 в качестве примера приведены результаты применения операций к массивам

A = [0 1 1 0 1];B = [1 1 0 0 1].

Укороченные логические операции выполняются над скалярами. Уко­роченными они названы, потому что их вычисление производится не полно­стью, а только до выяснения значения результата. Так, если в выражении А&&B первый оператор равен значению ложь, то значение выражения не зави­сит от В, и В не вычисляется. Укороченные операторы представлены в таблице П.5.

Таблица П.4. Поэлементные логические операции

Оператор	Описание	Пример
&	Возвращает 1, если соответствующие элементы обоих исходных массивов имеют значение истина (не равны нулю), и 0 в других ситуациях.	A & B = 01001
|	Возвращает 1, если хотя бы один из соответст­вующих элементов исходных массивов имеет значение истина (не равен нулю), и 0 в против­ном случае.	A | B = 11101
~	Инвертирует каждый элемент исходного мас­сива	A~A = 10010
xor	Возвращает 1в том случае, если соответствую­щие элементы исходных массивов не равны, и 0 в противном случае.	xor(A,B)= 10100

Таблица П.5. Укороченные логические операции

Оператор	Описание
&&	Возвращает значение истина (1), если оба операнда имеют значение истина (не равны нулю), и ложь (0) в противном случае.
||	Возвращает значение истина (1), если хотя бы один операнд имеет значение истина (не равен нулю), и ложь (0) в противном случае.

Для составления выражения необходимо знать очередность выполнения операций. Ниже операции перечислены в порядке убывания приоритета, в одном пункте операции одинакового приоритета:

1. Скобки ().

2. Транспонирование (.'), возведение в степень (.^), комплексно-сопряженное транспонирование ('), матричное возведение в степень (^).

3. Унарный плюс (+), унарный минус (-), логическое отрицание (~).

4. Умножение (.*), правое деление (./), левое деление(.\), матричное умножение (*), матричное правое деление (/), матричное левое деление (\).

5. Сложение (+), вычитание (-).

6. Оператор двоеточия (:).

7. Меньше (<), меньше или равно (<=), больше (>), больше или равно (>=), равно (==), не равно (~=).

8. Поэлементное И (&).

9. Поэлементное ИЛИ (|).

10. Укороченное И (&&).

11. Укороченное ИЛИ (||).

Для изменения порядка выполнения операций можно использовать круглые скобки.

БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ

1. Помощь MATLAB

2. Материалы Web-сайта exponenta.ru

3. Сборник задач по базовой компьютерной подготовке. Зубов В.С., Котарова И.Н., Архипов О.Г. и др. – М.: Изд-во МЭИ, 1998. – 178 с.

4. Маран М.М. Delphi. Начальный курс. М. изд-во МЭИ, 2002. –100 с.

5. Батасова В.С. Сборник заданий по программированию. – М.: Изд-во МЭИ, 2000. – 48 с.

Содержание

Введение....................................................................................................... 3

Лабораторная работа №1.