
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон повного струму. Використання закону повного струму для розрахунку магнітного поляСодержание книги
Поиск на нашем сайте
Скористаємось рівнянням Максвелла для циркуляції вектора напруженості магнітного поля
де j – густина струму провідності вільних електричних зарядів; У провідниках, в яких є вільні електричні заряди, струм зміщення відсутній (він може існувати лише у діелектричному середовищі), тобто
У цьому випадку рівняння (13.1.1) набуває вигляду:
Рівняння (13.1.2) називається законом повного струму. Для написання закону повного струму через індукцію магнітного поля слід замінити Н у формулі (13.1.2) на
Закон повного струму у цьому випадку матиме вигляд
Рівняння (13.1.3) формулюється так:
Циркуляція вектора індукції магнітного поля уздовж довільного замкнутого контуру дорівнює алгебраїчній сумі всіх струмів, охоплених цим контуром і помноженій на mm0.
Як видно з рівняння (13.1.3)
Таке магнітне поле називається вихровим. Силові лінії магнітного поля є завжди замкнутими.
Скористаємось законом повного струму (13.1.3) для розра-хунку магнітного поля соленоїда і тороїда.
а) знайдемо циркуляцію вектора В вздовж замкнутого контуру ABCD (рис.13.1). У нашому випадку витки в соленоїді щільно прилягають один до одного. Соленоїд має довжину, значно більшу за діаметр.
Рис.13.1
На ділянках DA і BC На ділянці CD Тому з урахуванням цих зауважень маємо:
де N – число витків, які вкладаються в інтервалі довжини соленоїда АВ; І – струм, який протікає в цих витках. Але
Звідки індукція магнітного поля на осі довгого соленоїда буде дорівнювати:
Вираз (13.1.6) показує, що на осі довгого соленоїда зі струмом І індукція магнітного поля дорівнює:
В = mm0nI.
б) магнітне поле на осі тороїда.
Розглянемо тороїд, який має вигляд довгого соленоїда, кінець і початок якого збігаються (рис.13.2).
Рис.13.2
Витки в такій котушці щільно прилягають один до одного, а радіус осьової лінії R. Знайдемо циркуляцію вектора
де N - число витків у тороїді; І - струм у витках.
Але
де Таким чином, індукція магнітного поля на осі тороїда визначається такою ж формулою, що і для довгого соленоїда, тобто
В = mm0nI. (13.1.7)
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 , (13.1.1)
, (13.1.1)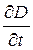 - струм зміщення, не пов’язаний з наявністю вільних електричних зарядів; Н – напруженість магнітного поля.
- струм зміщення, не пов’язаний з наявністю вільних електричних зарядів; Н – напруженість магнітного поля.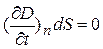 .
.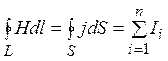 . (13.1.2)
. (13.1.2) .
. . (13.1.3)
. (13.1.3) .
.
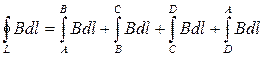 .
.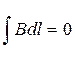 ; Тут
; Тут  а
а 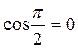
 ; Цю ділянку можна вибрати досить далеко від соленоїда, де магнітне поле відсутнє.
; Цю ділянку можна вибрати досить далеко від соленоїда, де магнітне поле відсутнє. . (13.1.4)
. (13.1.4)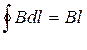 , де l = AB. Закон повного струму в цьому випадку перепишеться:
, де l = AB. Закон повного струму в цьому випадку перепишеться: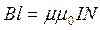 . (13.1.5)
. (13.1.5) . (13.1.6)
. (13.1.6)
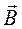 вздовж осьової лінії тороїда
вздовж осьової лінії тороїда ,
,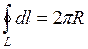 - довжина кола вздовж осьової лінії, тому
- довжина кола вздовж осьової лінії, тому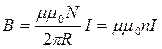 ,
, - число витків на одиницю довжини осьової лінії тороїда.
- число витків на одиницю довжини осьової лінії тороїда.


