
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зв’язок між потенціалом і напруженістю електростатич-ного поля. Приклади розрахунку полівСодержание книги
Поиск на нашем сайте
Як уже показано вище, робота переміщення одиничного позитивного заряду qo в полі заряду q, виконується за рахунок зменшення потенціальної енергії, тобто
А1,2 = П1 – П2 = -(П2 – П1) = -q(j2 - j1).
Запишемо цю роботу для безмежно малого переміщення, на якому електричний потенціал змінюється на безмежно малу величину
dА = -qodj, і dА = qo
Прирівняємо праві сторони рівностей (7.3.1), одержимо зв’язок між потенціалом і напруженістю електростатичного поля:
звідки E = -
Сам потенціал dj є величиною скалярною, а градієнт зміни потенціалу в певному напрямі є величиною векторною. В більш загальному випадку просторового переміщення точкового заряду формула (7.3.2) набуває вигляду
де Оператор
де Знайдемо різницю потенціалів j2 - j1, в двох точках поля біля безмежної поверхні з поверхневою густиною зарядів s у відповідності з рисунком (рис.7.4)
Рис 7.4
Скористаємося формулою (7.3.2) зв’язку напруженості електрич-ного поля з потенціалом, одержимо
dj = -Edr. (7.3.4)
Напруженість поля E біля безмежної поверхні розрахована в шостій лекції (6.3.3), тому скористаємось готовим результатом, який дорівнює E = Тоді dj = -
Інтегруємо цей вираз в межах зміни координати від x1 до x2 і зміни потенціалу від φ1 до φ2, одержимо
звідки j2 - j1 = - або j1 - j2 =
2. Потенціали поля в двох точках біля довгого, рівномірно зарядженого стрижня з лінійною густиною зарядів t у відповідності з рисунком (рис. 7.5)
Рис 7.5
На довільній відстані x від стрижня напруженість електричного поля розраховується або за принципом суперпозиції (методом інтегрування), або за теоремою Гаусса. Скористаємось готовою формулою напруженості електричного поля (6.3.15) попередньої лекції E =
Підставимо це значення напруженості у формулу (7.3.2) та виконаємо інтегрування dj = - або
звідки j1 - j2 =
Аналогічно можуть бути виконані і будь-які інші розрахунки різниці потенціалів електричного поля статичних зарядів.
ЛЕКЦІЯ 8 ЕЛЕКТРИЧНЕ ПОЛЕ В ПРОВІДНИКУ. ЕЛЕКТРОЄМНІСТЬ Провідник в електростатичному полі. Розподіл зарядів у провіднику. Електроємність окремого провідника. Конденсатори. Електроємність конденсаторів різної форми. Енергія взаємодії електричних зарядів. Енергія окремого провідника й конденсатора. Енергія електростатичного поля. Густина енергії електростатичного поля.
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.232.145 (0.011 с.) |

 . (7.3.1)
. (7.3.1) = -dj,
= -dj, . (7.3.2)
. (7.3.2) = -
= -  j = -
j = -  j,
j,
 +
+ 
 +
+ 
 , (7.3.3)
, (7.3.3)
 .
.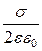 dr.
dr. = -
= - 
 ,
, (x2 – x1). (7.3.5)
(x2 – x1). (7.3.5)
 .
.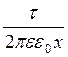 dx, (7.3.6)
dx, (7.3.6) = -
= - 
 ,
,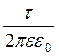 ln
ln  . (7.3.7)
. (7.3.7)


