
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рух точки по колу. Кутова швидкість і кутове прискорення
Довільний криволінійний рух можна подати як рух по дугах кіл. Тому зупинимося на кінематиці обертального руху, або руху точки вздовж колової траєкторії. У даному випадку зручно користуватись полярною системою координат, координатами якої є радіус кола R і кут повороту радіуса відносно вибраного напрямку j. В цьому випадку R – відстань від центра кола до точки на коловій траєкторії, а j - полярний кут (кут обертання)
Рис.1.3
З рис. 1.3 видно, що Кутова швидкість – векторна величина, яка дорівнює зміні кута повороту радіуса - вектора
Напрям вектора Кутове прискорення – векторна величина, яка дорівнює зміні кутової швидкості з часом, тобто
Напрям вектора кутового прискорення направлений по осі обертання (рис. 1.3). Вектор кутового прискорення руху точки по колу Модуль вектора лінійної швидкості точки
У векторній формі вектор швидкості
З визначення векторного добутку модуль вектора швидкості
ê
де a - кут між векторами Для рівномірного обертання матеріальної точки по коловій траєкторії модуль кутової швидкості дорівнює
Рис.1.4
Рівномірний рух по колу можна характеризувати також періодом обертання Т, тобто часом, за який точка здійснює один повний оберт, 2p = wТ. Звідки
Частота обертання визначається числом повних обертів, які здійснює точка при русі по колу, за одиницю часу:
При рівноприскореному обертальному русі b = const. Тому формули кінематики обертального руху точки матимуть вигляд:
Рівноприскорений обертальний рух характеризується дотичним й нормальним або доцентровим прискореннями:
у векторній формі
Зв’язок пройденого шляху по дузі кола з кутом повороту визначається так:
Тангенціальне й нормальне прискорення. Зв’язок між кінематичними величинами криволінійного руху Розглянемо нерівномірний криволінійний рух матеріальної точки. За малий проміжок часу Dt лінійна швидкість точки змінюється від
Рис.1.4
Вектори лінійної швидкості
У цьому випадку миттєве прискорення точки буде дорівнювати
В граничному випадку при Dt®0,
і
У випадку, коли вектори
З цього співвідношення отримуємо:
і
Напрямки векторів
Із цих міркувань можна зробити такі висновки: - нормальне й тангенціальне прискорення точки зростають лінійно із зростанням відстані точки до осі обертання; - вектор дотичного або тангенціального прискорення завжди збігається з дотичною до колової траєкторії; - вектор нормального прискорення направлений від точки на коловій траєкторії в стророну центра кола.
ЛЕКЦІЯ 2
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 799; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.69 (0.01 с.) |

 - кутове переміщення – векторна величина, модуль якої дорівнює куту повороту радіуса вектора
- кутове переміщення – векторна величина, модуль якої дорівнює куту повороту радіуса вектора  за час dt. Напрям цього вектора збігається з напрямком поступального руху правого гвинта.
за час dt. Напрям цього вектора збігається з напрямком поступального руху правого гвинта. з часом, тобто
з часом, тобто . (1.2.1)
. (1.2.1) збігається з напрямком
збігається з напрямком  . Одиницею вимірювання кутової швидкості є рад/с.
. Одиницею вимірювання кутової швидкості є рад/с. . (1.2.2)
. (1.2.2) збігається з напрямком
збігається з напрямком  . Для сповільненого обертання вектор
. Для сповільненого обертання вектор  має протилежний напрям до вектора
має протилежний напрям до вектора 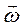 . Вимірюється кутове прискорення у рад/с2.
. Вимірюється кутове прискорення у рад/с2. , напрям якої збігається з дотичною до кола, зв’язаний з модулем вектора кутової швидкості
, напрям якої збігається з дотичною до кола, зв’язаний з модулем вектора кутової швидкості  . (1.2.3)
. (1.2.3) і
і 
 . (1.2.4)
. (1.2.4)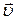 визначається співвідношенням
визначається співвідношенням ê =wR sina, (1.2.5)
ê =wR sina, (1.2.5) , як це показано на рис. 1.4.
, як це показано на рис. 1.4. . (1.2.6)
. (1.2.6)
 . (1.2.7)
. (1.2.7) . (1.2.8)
. (1.2.8) . (1.2.9)
. (1.2.9) ;
; ,
, . (1.2.10)
. (1.2.10) . (1.2.11)
. (1.2.11) до
до  у відповідності з рисунком.
у відповідності з рисунком.
 і
і  змінюється як за величиною, так і за напрямком. З рис.1.4. видно, що
змінюється як за величиною, так і за напрямком. З рис.1.4. видно, що . (1.3.1)
. (1.3.1) . (1.3.2)
. (1.3.2) , де
, де
 . (1.3.3)
. (1.3.3) змінюються з часом, зв’язок між кінематичними величинами знаходять шляхом диференціювання за часом векторного добутку
змінюються з часом, зв’язок між кінематичними величинами знаходять шляхом диференціювання за часом векторного добутку  , тобто
, тобто . (1.3.4)
. (1.3.4)
 . (1.3.5)
. (1.3.5) а також
а також  і
і  є взаємно перпендикулярними.
є взаємно перпендикулярними.


