
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Діелектрику. Діелектрична проникністьСодержание книги
Поиск на нашем сайте
Розглянемо діелектрик, який розміщено між пластинами конденсатора, площа яких досить велика порівняно з відстанню між пластинами. Лише при цій умові електричне поле в центральній частині конденсатора можна вважати однорідним (рис. 9.7). З рисунка видно, що електричне поле
Рис.9.7
В діелектрику поля
В скалярній формі
| де Скористаємося теоремою Гаусса до замкнутої поверхні у вигляді циліндра з стороною h паралельною до вектора
де Е = Е0 -
З урахуванням того, що Е¢ і Рn мають протилежні знаки, одержимо (рис. 9.7)
Помножимо рівняння (9.2.1) на e0, одержимо:
Величину в дужках в лівій частині рівняння називають вектором електричного зміщення і позначають буквою
Вектор електричного зміщення визначається лише вільними зарядами і не залежить від властивостей діелектрика. Теорема Гаусса для поля в діелектрику буде мати вигляд
Із викладеного вище відомо, що
Підставимо величину вектора поляризації
Величину 1+c у співвідношенні (9.2.5) називають відносною діелектричною проникністю середовища і позначають буквою e, тобто
e= 1+c. (9.2.6)
З урахуванням (9.2.6) вектор електричного зміщення буде мати вигляд
Для вакууму e =1; в діелектричному середовищі e >1. Фізично відносна діелектрична проникність середовища показує у скільки разів напруженість електричного поля у вакуумі більша за напруженість цього ж поля у деякому діелектричному середовищі.
9.3. Поле в діелектрику. Умови на межі двох діелектриків
Розглянемо плоский конденсатор, заповнений діелектриком (рис.9.8).
Рис.9.8
На рисунку s - поверхнева густина вільних електричних зарядів на обкладках конденсатора; s¢ - поверхнева густина зв’язаних зарядів діелектрика. В цьому випадку
в той же час
Для поля в діелектрику одержимо співвідношення
Напруженість поля у діелектрику збігається з напруженістю поля у вакуумі у випадку рівності s = s¢. Для вимірювання поля у діелектрику достатньо виміряти різницю потенціалів на обкладках конденсатора і відстань між пластинами конденсатора. У цьому випадку
Розглянемо умови на межі двох діелектриків. На межі поділу двох діелектриків з різними діелектричними проникностями вектори
Рис.9.10
Поблизу межі поділу в кожному із діелектриків електричні поля створені лише зв’язаними зарядами. Ці поля орієнтовані в різних напрямках. Результуюче поле
Скористаємось теоремою Гаусса для розрахунку потоку напруженості електричного поля крізь замкнуту поверхню циліндра з торцями S і висотою h (всі розміри досить малі)
Тут вільні електричні заряди відсутні, а тому й права сторона співвідношення дорівнює нулю. Після інтегрування одержимо
Dn,2S = Dn,1S,
або Dn,2 = Dn,1 (9.3.4)
Нормальні складові електричного зміщення на межі поділу двох діелектриків не розриваються. З урахуванням того, що Dn,2 = e2e0En,2, а Dn,1 = e1e0En,1, одержуємо:
e2e0En,2 = e1e0En,1,
звідки
тому Еn,1 ¹ En,2 . (9.3.5)
Нормальні складові напруженостей електричного поля на межі поділу двох діелектриків розриваються. Для дослідження дотичних складових векторів
Рис. 9.11
У вибраному прямокутнику довжина сторони h наближено дорівнює нулю, тому
Після інтегрування одержимо
Дотичні складові вектора напруженості на межі поділу двох діелектриків не розриваються. Для дотичних складових вектора електричного зміщення будемо мати
Так як e1¹e2, то
Дотичні складові електричних зміщень розриваються на межі поділу двох діелектриків.
ЛЕКЦІЯ 10 ПОСТІЙНИЙ ЕЛЕКТРИЧНИЙ СТРУМ
|
||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.59.107 (0.009 с.) |

 , створюється вільними зарядами, розміщеними на пластинах конденсатора. Електричне поле
, створюється вільними зарядами, розміщеними на пластинах конденсатора. Електричне поле  створено зв’язаними електричними зарядами. Вектор поляризації
створено зв’язаними електричними зарядами. Вектор поляризації 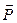 безпосередньо відноситься до вільних зарядів на пластинах конденсатора.
безпосередньо відноситься до вільних зарядів на пластинах конденсатора.
 і
і 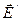 паралельні, тому результуюче поле визначається за допомогою принципу суперпозиції
паралельні, тому результуюче поле визначається за допомогою принципу суперпозиції
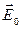 +
+ 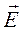 |=Е0-Е¢,
|=Е0-Е¢, .
.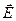 . Нехай висота циліндра h»0, тоді
. Нехай висота циліндра h»0, тоді ,
,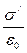 .
.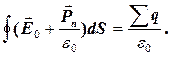 (9.2.1)
(9.2.1)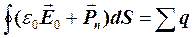 . (9.2.2)
. (9.2.2)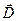 .
. . (9.2.3)
. (9.2.3) . (9.2.4)
. (9.2.4) =ceо
=ceо 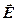 о.
о. у співвідношення (9.2.3), одержимо
у співвідношення (9.2.3), одержимо . (9.2.5)
. (9.2.5)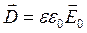 (9.2.7)
(9.2.7)
 ,
,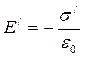 .
. . (9.3.1)
. (9.3.1) . (9.3.2)
. (9.3.2)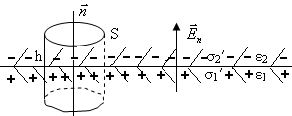
 в цьому випадку буде дорівнювати
в цьому випадку буде дорівнювати =
= 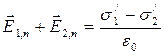 . (9.3.3)
. (9.3.3) .
. ,
,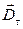 і
і  на межі поділу двох діелектриків можна скористатися теоремою про циркуляцію вектора
на межі поділу двох діелектриків можна скористатися теоремою про циркуляцію вектора 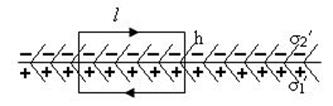
 .
.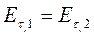 .
. .
. .
.


