
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменти інерції найпростіших тіл показані в таблиці 1.Содержание книги
Поиск на нашем сайте
Таблиця 1
Моментом імпульсу матеріальної точки масою mi називається векторний добуток радіуса-вектора
За означенням напрям вектора моменту імпульсу визначають за правилом векторного добутку. На рис. 4.7 показано напрям вектора моменту імпульсу матеріальної точки, який збігається з напрямком поступального руху правого гвинта.
Рис.4.7
Момент імпульсу твердого тіла знаходять за допомогою додавання моментів імпульсу всіх матеріальних точок тіла:
або
Знайдемо похідну за часом від рівняння (4.3.1)
де
З урахуванням всіх позначень рівність (4.3.4) набуває вигляду
Підсумувавши цю рівність для всіх матеріальних точок твердого тіла, одержимо
Рівність (4.3.3) для твердого тіла дає величину моменту імпульсу тіла, який дорівнює
Таким чином для твердого тіла виконується рівність
або (4.3.8)
Рівності (4.3.8) у фізиці називають основним рівнянням динаміки обертального руху. В цих рівностях І – скалярна величина, яка є мірою інертності тіл при обертальному русі; Основне рівняння динаміки обертального руху відіграє таку ж роль у динаміці обертального руху, що і другий закон Ньютона для поступального руху. Ці закони мають також однакову форму написання.
Знайдемо вираз для кінетичної енергії обертального руху матеріальної точки або твердого тіла. Скористаємося формулою кінетичної енергії поступального руху матеріальної точки або твердого тіла:
де Якщо тіло здійснює поступальний і обертальний рухи, то його повна кінетична енергія буде дорівнювати сумі кінетичних енергій поступального й обертального рухів
де І – момент інерції тіла відносно вибраної осі обертання; u – швид-кість руху центра мас цього тіла. Зіставивши вирази кінетичної енергії поступального й обертального рухів, робимо висновок, що мірою інертності при обертальному русі є момент інерції тіла. Розглянемо рух матеріальної точки або твердого тіла по коловій траєкторії у відповідності з рис. 4.8.
Рис. 4.8 За безмежно малий час матеріальна точка під дією сили F здійснює переміщення по дузі dS, довжина якої дорівнює rdj. При цьому виконується механічна робота
dA = FdS = Fr dj = M dj. (4.3.13)
Потужність у цьому випадку буде дорівнювати
де М – момент діючої сили; w - кутова швидкість. Потужність є скалярною величиною, тому
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.42.122 (0.009 с.) |









 на вектор імпульсу
на вектор імпульсу  цієї точки
цієї точки = [
= [  ]. (4.3.1)
]. (4.3.1)
 , (4.3.2)
, (4.3.2) . (4.3.3)
. (4.3.3) , (4.3.4)
, (4.3.4) , так як це однонапрямлені вектори;
, так як це однонапрямлені вектори; - сила у відповідності з другим законом Ньютона;
- сила у відповідності з другим законом Ньютона;  - момент сили, діючий на і-ту матеріальну точку.
- момент сили, діючий на і-ту матеріальну точку. . (4.3.5)
. (4.3.5) . (4.3.6)
. (4.3.6) . (4.3.7)
. (4.3.7) ,
, .
. - кутове прискорення – векторна величина, напрям якого збігається з напрямком поступального руху правого гвинта. Вектор моменту імпульсу
- кутове прискорення – векторна величина, напрям якого збігається з напрямком поступального руху правого гвинта. Вектор моменту імпульсу  направлений за напрямком вектора кутового прискорення.
направлений за напрямком вектора кутового прискорення. , або
, або  , або
, або  . (4.3.9)
. (4.3.9) , або
, або  , або
, або  . (4.3.10)
. (4.3.10) . (4.3.11)
. (4.3.11) ;
;  - момент інерції твердого тіла відносно осі обертання.
- момент інерції твердого тіла відносно осі обертання. , (4.3.12)
, (4.3.12)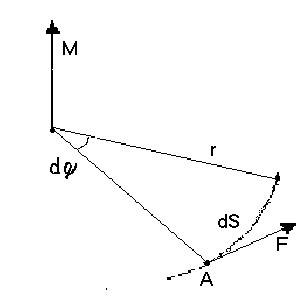
 , (4.3.14)
, (4.3.14) . (4.3.15)
. (4.3.15)


