
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Електротехнічних спеціальностейСтр 1 из 28Следующая ⇒
С.Г.Авдєєв, Т.І.Бабюк ЛЕКЦІЇ З ФІЗИКИ Навчальний посібник для студентів бакалаврських напрямків Електротехнічних спеціальностей (механіка, електрика, електромагнетизм)
Міністерство освіти і науки України Вінницький національний технічний університет
С.Г. Авдєєв, Т.І. Бабюк
ЛЕКЦІЇ З ФІЗИКИ
Навчальний посібник для студентів бакалаврських напрямків Електротехнічних спеціальностей (механіка, електрика, електромагнетизм)
Затверджено Ученою радою Вінницького державного технічного університету як навчальний посібник для студентів бакалаврського напрямку електротехнічних спеціальностей. Протокол №11 від 25 червня 2003 року
Вінниця ВНТУ 2003 ПЕРЕДМОВА Рух точки по колу. Кутова швидкість і кутове прискорення. Тангенціальне й нормальне прискорення. Зв’язок між кінематичними величинами криволінійного руху Розглянемо нерівномірний криволінійний рух матеріальної точки. За малий проміжок часу Dt лінійна швидкість точки змінюється від
Рис.1.4
Вектори лінійної швидкості
У цьому випадку миттєве прискорення точки буде дорівнювати
В граничному випадку при Dt®0,
і
У випадку, коли вектори
З цього співвідношення отримуємо:
і
Напрямки векторів
Із цих міркувань можна зробити такі висновки: - нормальне й тангенціальне прискорення точки зростають лінійно із зростанням відстані точки до осі обертання; - вектор дотичного або тангенціального прискорення завжди збігається з дотичною до колової траєкторії; - вектор нормального прискорення направлений від точки на коловій траєкторії в стророну центра кола.
ЛЕКЦІЯ 2
Динаміка поступального руху точки Перший закон Ньютона. Маса. Сила. Другий закон Ньютона. Рівняння руху точки. Другий закон Ньютона. Рівняння руху точки
Другий закон Ньютона є основним законом динаміки. Він виконується лише в інерційних системах відліку. Це фундаментальний закон природи, которий є узагальненням багатьох дослідних фактів. Формулюється другий закон Ньютона так: Прискорення, набуте матеріальною точкою або тілом, пропорційне рівнодійній всіх діючих сил і обернено пропорційне масі матеріальної точки або тіла.
Більш загальне формулювання другого закону Ньютона таке:
ЛЕКЦІЯ 3 МЕХАНІЧНА ЕНЕРГІЯ 3.1.Механічна робота, як міра зміни енергії. Потужність. Кінетична енергія. 3.2.Консервативні й неконсервативні сили. Потенціальна енергія. Зв’язок роботи й потенціальної енергії. 3.3.Сила й потенціальна енергія. Поняття градієнта. 3.4.Закон збереження й перетворення механічної енергії.
3.1. Механічна робота, як міра зміни енергії. Потужність. Кінетична енергія
Енергія – це універсальна міра руху різних форм матерії. З різними формами руху матерії пов’язані різні форми енергії: механічна, теплова, електромагнітна, ядерна та ін. Будь-які зміни механічного руху визиваються силами, що діють із сторони інших тіл. Фізична величина, яка чисельно дорівнює скалярному добутку векторів сили
де У загальному випадку дія сили може змінюватись як за величиною, так і за напрямком, тому в таких випадках формулою (3.1.1) користуватися не можна. На безмежно малому переміщенні
Робота змінної сили визначається за допомогою інтеграла:
Одиницею вимірювання роботи в системі СІ є джоуль (Дж)
Розглянемо найбільш загальний випадок руху матеріальної точки уздовж криволінійної траєкторії L. Умовно поділимо пройдений шлях на безмежно малі ділянки шириною dx, на яких силу F може вважати сталою величиною (рис. 3.1). Елементарна робота на таких безмежно малих переміщеннях може бути розрахована за формулою
Рис.3.1
Якщо скласти всі елементарні роботи, то одержимо вираз для знаходження повної роботи у вигляді криволінійного інтеграла уздовж криволінійної траєкторії
Робота сили, виконана за одиницю часу, називається потужністю. Потужність – це швидкість виконання механічної роботи. Тому
Одиницею вимірювання потужності є ват (Вт). Один Вт дорівнює 1Дж/с. Оскільки
то формулу для роботи можна переписати у вигляді
тобто роботу можна виразити через інтеграл від потужності й часу, а також через скалярний добуток вектора сили й вектора швидкості. В останньому випадку сила, перпендикулярна до вектора швидкості, роботи не виконує. З урахуванням другого закону Ньютона
Оскільки
Якщо швидкість матеріальної точки в процесі руху змінюється від u1 до u2 , то робота, яка виконується у цьому випадку, буде дорівнювати
Скалярна величина Слід також пам’ятати, що в цьому прикладі ми мали справу з повною силою, діючою на точку. Так, у випадку переміщення саней уздовж не дуже гладенької дороги, посипаної піском, виконується робота, відмінна від нуля. Приросту кінетичної енергії тут не буде. Вся справа в тому, що сила опору руху саней має протилежний напрям. Робота цієї сили має від’ємний знак. Сила тертя теж виконує роботу, але від’ємну. А в результаті повна сила і повна робота виявляються рівними нулю.
3.2. Консервативні й неконсервативні сили. Потенціальна енергія. Зв’язок роботи й потенціальної енергії
Всі сили, які зустрічаються в механіці макроскопічних тіл, прийнято поділяти на консервативні й неконсервативні. До консервативних сил відносяться такі сили, робота яких не залежить від форми шляху між двома точками 1 і 2 (рис. 3.2).
A1,2(a)=A1,2(b)=A1,2(c)
Рис.. 3.2
Прикладом консервативних сил є сила тяжіння Землі. Робота сили тяжіння при перенесенні матеріальної точки із положення 1 в положення 2, уздовж прямолінійного відрізку
Рис. 3.3
де h1 і h2 - висоти, на яких перебувала матеріальна точка на початку і в кінці шляху. Вираз роботи (3.2.1) справедливий для переміщення з точки 1 в точку 2 на будь-якому шляху. Ще одним прикладом консервативних сил є так звані центральнісили. Прикладом центральних сил можуть бути гравітаційні сили планет і зірок, кулонівські сили точкових зарядів обох знаків, ядерні сили (на дуже малих відстанях) тощо. Покажемо, що робота центральних сил не залежить від форми шляху. Знайдемо роботу сили гравітаційного притягання двох точкових мас m і М у випадку переміщення точкової маси m з точки 1 в точку 2 в гравітаційному полі точкової маси М (рис. 3.4.).
Рис. 3.4
В даних перетвореннях
Введемо поняття потенціальної енергії, як частини механічної енергії, яка залежить від взаємного розміщення матеріальних точок (тіл) у силовому полі. Силове поле називається потенціальним, якщо робота переміщення точки в цьому полі не залежить від форми шляху. В потенціальних полях діють лише консервативні сили.
Потенціальна енергія чисельно дорівнює роботі переміщення матеріальної точки (тіла) з даної точки простору в деяке фіксоване або нульове положення. Точка ”О” на рис. 3.5. є фіксованою. Знайдемо роботу переміщення матеріальної точки з положення М1 в положення М2. Для цього спочатку знайдемо роботу переміщення точки (тіла) з точки “М1” в точку “О” і з точки “М2” в точку “О”.
Рис. 3.5.
В цих розрахунках П1 і П2, згідно з визначенням, є потенціальними енергіями матеріальної точки (тіла) в точках М1 і М2 простору. Тому робота консервативних сил в потенціальних полях може бути виражена через втрату (зменшення) потенціальної енергії
При заміні одного нульового положення іншим, потенціальна енергія змінюється на постійну величину. Таким чином, потенціальна енергія визначається неоднозначно, а з точністю до деякої константи. Однак це не впливає на кінцеві результати, так як в цьому випадку є важливою лише різниця потенціальних енергій dП. Прикладами потенціальної енергії у деяких найпростіших випадках є: П=mgh – потенціальна енергія однорідного поля тяжіння; П= П =
3.3.Сила й потенціальна енергія. Поняття градієнта
Зв’язок сили й потенціальної енергії знайдемо із співвідношення (3.2.6)
Потенціальна енергія є скалярною величиною. Однак її зміна в певному напрямі є векторною величиною. Зміна потенціальної енергії в певному напрямі називається градієнтом, тобто
В рівності (3.2.8) вектором є градієнт. Для руху матеріальної точки (тіла) в тривимірному просторі градієнт потенціальної енергії повинен враховувати проекції на осі координат х, у, z, тобто
де Вираз (3.2.9) також можна записати через оператор набла, тобто
де -
В формулі (3.2.10) потенціальна енергія є скалярною величиною, а ось диференціювання скалярної величини по координатним осям дає вектор.
Вирази оператора набла
Градієнт скалярної величини П є вектор, який направлений вздовж нормалі в сторону зростання функції Пz (рис.3.6).
Рис. 3.6.
Поверхні однакової потенціальної енергії називаються еквіпотенціальними поверхнями.
3.4. Закон збереження й перетворення механічної енергії
Сума кінетичної і потенціальної енергії всіх тіл, які складають замкнуту систему і взаємодіють між собою лише консервативними силами, залишається незмінною. Це твердження виражає собою закон збереження й перетворення енергії в механічних процесах. Якщо між тілами, які входять до замкнутої системи, будуть діяти сили тертя, то механічна енергія не зберігається. Частина її перетворюється у внутрішню енергію нагрівання тіл. Розглянемо замкнуту систему матеріальних точок масами m1, m2, m3,..., mn, які рухаються з швидкостями відповідно v1, v2, v3, …,vn під дією внутрішніх консервативних сил f1, f2 , f3,…, fn. Запишемо для всіх тіл цієї системи ІІ-й закон Ньютона:
Нехай за час dt кожна із точок системи здійснює відповідне переміщення Помножимо рівності (3.4.1) на відповідні їм переміщення, одержимо:
Склавши всі ці рівняння в одно, одержимо
або
В рівності (3.4.3) під знаками сум є безмежно малі зміни відповідно кінетичної і потенціальної енергій, тобто
В рівності (3.4.4) враховано, що робота консервативних сил виконується за рахунок зменшення потенціальної енергії (рівність 3.2.6), або
де
З урахуванням цих зауважень одержуємо:
d(К+П)=0, звідки К+П=const. (3.4.6)
Повна механічна енергія всіх тіл замкненої системи з часом не змінюється. В межах замкнутої системи відбувається перетворення енергії з одного виду в інший. Системи тіл, в яких спостерігається перетворення енергії в інші, не механічні види енергії, називаються дисипативною. Однак і в цьому випадку відповідна еквівалентність між енергіями обов’язково зберігається.
Короткий висновок: Таким чином, енергія ніколи не зникає безслідно і не виникає, вона лише перетворюється із одного виду в інший у рівновеликих кількостях. У цьому твердженні полягає основна фізична суть закону збереження і перетворення механічної енергії – суть не зникнення матерії та її руху.
ЛЕКЦІЯ 4
Теорема Штейнера Розглянемо приклади розрахунку моментів інерції найпростіших тіл. Момент інерції суцільного диска. Розглянемообертання диска масою m і радіусом R відносно осі, яка проходить через центр мас диска, перпендикулярно до його площини, як це показано на рис. 4.2.
Рис. 4.2
Момент інерції заштрихованої частини диска з масою dm і радіусом r у відповідності з (4.1.3) буде дорівнювати
Маса заштрихованої частини диска дорівнює
Елемент маси dm (4.2.2) підставимо в (4.2.1) і інтегруємо по радіусу диска
де h – товщина диска; r - густина речовини диска. Таким чином момент інерції диска відносно осі обертання, перпендикулярної до площини диска, дорівнює
I д =
Момент інерції стержня відносно осі обертання, яка проходить через кінець стержня, перпендикулярно до його довжини. Маса стержня m, а довжина l (рис.4.3).
Рис. 4.3
Для знаходження моменту інерції стержня скористаємося формулою (4.2.1)
dI=dmx2 ,
де dm=Sdxr - маса виділеного елемента; S – переріз стержня; r - густина речовини стержня; dx – довжина виділеного елемента стержня. Інтегруємо цей вираз по довжині стержня, одержимо
Таким чином знайдена величина моменту інерції стержня відносно осі, яка проходить через кінець стержня, перпендикулярно до його довжини, буде дорівнювати
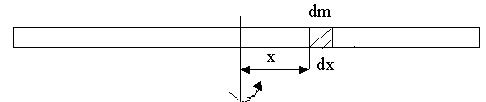
Момент інерції стержня відносно осі, яка проходить через центр мас, перпендикулярно до його середини (рис.4.3)
Рис.4.4
Момент інерції безмежно малого елемента стержня відносно осі, показаної на рисунку, дорівнює
dI=dm x2,
де dm = Sdxr - маса заштрихованого елемента. З урахуванням цієї маси момент інерції елемента стержня буде дорівнювати dI= Srx2 dx. (4.2.5)
Інтегруємо вираз (4.2.5) в межах від 0 до
Таким чином момент інерції стержня відносно осі, яка проходить через його центр мас (рис.4.4), дорівнює
Момент інерції кулі знайдемо відповідно до рис. 4.5.
Рис.4.5
Заштрихована частина кулі має форму диска радіусом у і товщиною dz. Момент інерції виділеного диска відповідно до (4.2.3) дорівнює
Маса виділеного диска радіусом у і товщиною dz буде дорівнювати
dm= py2rdz. (4.2.7)
Підставимо (4.2.7) у (4.2.6), одержимо
З рис.4.5 видно, що y2=R2-z2, тому
dI =
Інтегруємо цей вираз в межах z від 0 до R, урахувавши нижню частину кулі, не показану на рис. 4.5
Тобто момент інерції кулі масою m і радіусом R дорівнює
Ік =
У деяких випадках момент інерції твердого тіла відносно осі, яка не збігається з центром мас тіла, розраховують за теоремою Штейнера. Момент інерції тіла І відносно довільної осі ОО1 дорівнює сумі моменту інерції цього тіла відносно паралельної осі Іс, яка проходить через центр мас, і добутку маси цього тіла на квадрат відстані між паралельними осями (рис. 4.6).
Рис. 4.6
I = Ic + ma2, (4.2.10)
де вираз (4.2.10) є теоремою Штейнера. Покажемо справедливість цієї теореми на прикладі розрахунку моментів інерції стержня, для якого Іс =
Рис. 4.7
що підтверджується попереднім незалежним виведенням методом інтегрування.
ЛЕКЦІЯ 5 Зв’язок маси й енергії.
5.1. Постулати спеціальної теорії відносності Закон складання швидкостей Розглянемо деякий процес, який відбувається у точці А, нерухомій відносно штрихованої системи координат. Позначимо тривалість деякого процесу за годинниками не штрихованої системи й штрихованої системи відповідно через t і tо. Очевидно, що
Для знаходження залежності tо від t скористаємось перетвореннями координат Лоренца (5.1.7)
Віднімемо рівності (5.2.2), одержимо t0:
тому
З рівності (5.2.3) знайдемо t
Висновок. Якщо v»c, то t0<<t. Час в різних системах відліку протікає не однаково. Одна і та ж подія має різну тривалість у різних системах відліку.
Знайдемо довжину рухомого предмета в різних системах відліку. Нехай стрижень, який має довжину l0 в штрихованій системі координат, рухається разом з цією системою координат з швидкістю u відносно не штрихованої системи координат (рис. 5.2). (Стрижень перебуває у спокої відносно штрихованої системи координат). Як видно з рисунка, довжина стрижня у штриховій системі координат дорівнює:
Рис. 5.2
Координати
Звідки
Висновок. Якщо швидкість руху стрижня для спостерігача, який перебуває у стані спокою в системі координат x, y, z прямує до швидкості світла, то l ®0. Лінійні розміри тіла, яке рухається з швидкістю близькою до швидкості світла, в різних системах відліку будуть різними.
Для знаходження закону складання швидкостей, запишемо перетворення координат Лоренца (5.1.7) через безмежно малі зміни координат x, x’ і часу t і t’, тобто
Поділивши (5.2.7) на (5.2.8), одержимо
Введемо позначення
Нехай швидкість штрихованої системи координат u®c, швидкість матеріальної точки в штрихованій системі
Цей висновок є гарним доказом другого постулату Ейнштейна. Формула (5.2.10) є законом складання швидкостей у напрямі осі х. Аналогічно можна одержати відповідні співвідношення для інших осей координат. Зв’язок маси і енергії Релятивістська маса рухомого тіла залежить від швидкості руху
де m0 - маса спокою тіла; m – маса тіла в процесі руху з швидкістю u. Залежність маси тіла від швидкості руху в релятивістському випадку показана на рис. 5.3. З рисунка видно, що якщо u®c то m®∞.
Рис.5.3
Оскільки реальне тіло при наближенні швидкості його руху до швидкості світла збільшує свою масу до безмежності, то тіла реальної маси такої швидкості досягти не можуть. Швидкість світла мають лише фотони, маса спокою яких дорівнює нулю.
Релятивістський імпульс тіла, швидкість якого наближається до швидкості світла, має вигляд:
Релятивістський імпульс всіх тіл замкнутої системи з часом не змінюється. Цей висновок для закону збереження імпульсу є наслідком однорідності простору.
Релятивістський закон динаміки (другий закон Ньютона) матиме вигляд:
Якщо u<<c, то рівняння (5.3.3) трансформується у класичний закон динаміки
Повна енергія тіла масою m визначається співвідношенням:
де m – маса тіла в процесі руху з швидкістю
Енергія спокою тіла дорівнює Е0 = m0с2, тому співвідношення (5.3.5) перепишеться
Кінетичну енергію руху легко визначити, якщо від повної енергії тіла відняти енергію спокою цього тіла, тобто
Релятивістське співвідношення між повною енергією і релятивістським імпульсом тіла має вигляд
У випадку фотонів, маса спокою яких дорівнює нулю:
E2 - p2c2 =0, або
Тобто
ЛЕКЦІЯ 6 ЕЛЕКТРОСТАТИКА Рис. 6.7
З рисунка видно, що x2 = z2 + r2, а dq = rda drs, й dEz = dEcosj. З урахуванням цих позначень одержуємо:
Але оскільки соsj =
Інтегруємо цей вираз у межах: для r від 0 до
З розрахунків видно, що напруженість електричного поля біля безмежної, рівномірно зарядженої площини з поверхневою густиною зарядів s, визначається досить простою формулою і не залежить від відстані до самої площини
Приклад 2. Визначити напруженість електричного поля на відстані а від тонкої, досить довгої, рівномірно зарядженої, із лінійною густиною зарядів t нитки або циліндра (рис 6.8).
Рис. 6.8
Скористаємось формулою (6.2.6)
dE =
З рисунка видно, що: dq = tdl і dS = rda, а також dS = dl·cosa. З урахуванням цих залежностей одержуємо величину точкового заряду: dq =
Тоді напруженість електричного поля у напрямі осі у Ey – буде дорівнювати
dEy = dEcosa =
Величину радіуса-вектора r виразимо через відстань а і кут a: r =
З урахуванням останнього одержимо:
dEy =
Інтегруємо останній вираз у межах зміни a від 0 до
Таким чином одержано досить просту залежність напруженості електричного поля біля довгої, рівномірно зарядженої нитки або циліндра:
Е =
Паралельна складова напруженості Еx, завдяки симетричності нитки, буде дорівнювати нулю.
Знайдемо потік вектора
Рис. 6.9
де З рисунка видно, що
де Площа поверхні кулі Таким чином одержуємо:
Інтегруємо цей вираз у межах замкнутої поверхні і повного тілесного кута для цієї поверхні, тобто
Одержаний вираз носить назву теореми Гаусса
Якщо замкнута поверхня охоплює систему зарядів, теорема Гаусса набуде вигляду
Потік вектора напруженості електричного поля крізь довільну замкнуту поверхню дорівнює алгебраїчній сумі всіх зарядів у середині цієї поверхні, поділених на ee0. Покажемо на прикладах, як використовується теорема Гаусса у найпростіших випадках. Приклад 1. Електричне поле біля безмежної, рівномірно зарядженої, із поверхневою густиною зарядів σ, площини (рис. 6.10).
Рис. 6.10
На рисунку заряджена площина спроектована перпендикулярно до площини листка. Замкнена поверхня є циліндром із площею торців S. Потік вектора напруженості в даному випадку слід розрахувати лише крізь торці. Лінії напруженості електричного поля паралельні до бокової поверхні, а тому потоку не створюють, тобто
За теоремою Гаусса
Прирівнявши праві сторони (6.3.11) і (6.3.12) одержимо:
Цей висновок збігається з формулою (6.3.3).
Приклад 2. Електричне поле на відстані a від довгої, рівномірно зарядженої з лінійною густиною зарядів τ, нитки (рис. 6.11).
Рис. 6.11
На рисунку замкнуту поверхню вибрано у вигляді циліндра радіусом а і довжиною h. Потік силових ліній слід розглядати лише крізь бокову поверхню, так як торці перпендикулярні до нитки й паралельні до напрямку силових ліній електричного поля. (Потік крізь торці в цьому випадку дорівнює нулю).
За теоремою Гаусса
Прирівнюємо праві частини (6.3.13) і (6.3.14), одержимо
Звідки
що збігається з формулою (6.3.6)
Висновок. Теорема Гаусса значно спрощує розрахунки, але має дуже вузькі рамки використання. Більш загальним, універсальним методом розрахунків напруженості електричного поля є метод суперпозиції, який у кінцевому випадку зводиться до інтегрування.
ЛЕКЦІЯ 7
ПОТЕНЦІАЛ ЕЛЕКТРОСТАТИЧНОГО ПОЛЯ 7. 1. Циркуляція вектора напруженості.Теорема про циркуляцію вектора напруженості. Потенціальна енергія заряду. Рис 7.5
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.229.253 (0.461 с.) |
 до
до  у відповідності з рисунком.
у відповідності з рисунком.
 і
і  змінюється як за величиною, так і за напрямком. З рис.1.4. видно, що
змінюється як за величиною, так і за напрямком. З рис.1.4. видно, що . (1.3.1)
. (1.3.1) . (1.3.2)
. (1.3.2) , де
, де
 . (1.3.3)
. (1.3.3) змінюються з часом, зв’язок між кінематичними величинами знаходять шляхом диференціювання за часом векторного добутку
змінюються з часом, зв’язок між кінематичними величинами знаходять шляхом диференціювання за часом векторного добутку  , тобто
, тобто . (1.3.4)
. (1.3.4)
 . (1.3.5)
. (1.3.5) а також
а також  і
і  є взаємно перпендикулярними.
є взаємно перпендикулярними. , або
, або  . (2.2.1)
. (2.2.1) і переміщення
і переміщення  , називається механічною роботою.
, називається механічною роботою. ^
^  ), (3.1.1)
), (3.1.1)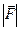 і
і  - модулі векторів сили і переміщення;
- модулі векторів сили і переміщення;  ^
^  силу
силу  можна вважати постійною. В цьому випадку величина елементарної роботи
можна вважати постійною. В цьому випадку величина елементарної роботи  A буде дорівнювати
A буде дорівнювати . (3.1.2)
. (3.1.2) . (3.1.3)
. (3.1.3) = Н·м = Дж.
= Н·м = Дж. . (3.1.4)
. (3.1.4)
 . (3.1.5)
. (3.1.5) . (3.1.6)
. (3.1.6) , (3.1.7)
, (3.1.7) , (3.1.8)
, (3.1.8) вираз для механічної роботи набуде вигляду:
вираз для механічної роботи набуде вигляду: . (3.1.9)
. (3.1.9) , а
, а  , то
, то . (3.1.10)
. (3.1.10) . (3.1.11)
. (3.1.11) називається кінетичною енергією. Таким чином ми довели, що робота сили по переміщенню матеріальної точки дорівнює зміні її кінетичної енергії.
називається кінетичною енергією. Таким чином ми довели, що робота сили по переміщенню матеріальної точки дорівнює зміні її кінетичної енергії.
 (рис.3.3) дорівнює:
(рис.3.3) дорівнює:
 , (3.2.1)
, (3.2.1)
 . (3.2.2)
. (3.2.2) . Тому
. Тому . (3.2.3)
. (3.2.3)
 ,
,  . (3.2.4)
. (3.2.4) . (3.2.5)
. (3.2.5) П, де dП= - (П2 – П1). (3.2.6)
П, де dП= - (П2 – П1). (3.2.6) - потенціальна енергія розтягнутої на величину х пружини (початкова точка х=0);
- потенціальна енергія розтягнутої на величину х пружини (початкова точка х=0); - потенціальна енергія гравітаційного притягання точкових мас m і М.
- потенціальна енергія гравітаційного притягання точкових мас m і М. , звідки
, звідки  . (3.2.7)
. (3.2.7) . (3.2.8)
. (3.2.8) , (3.2.9)
, (3.2.9) - одиничні вектори в напрямках координатних осей х,у, z;
- одиничні вектори в напрямках координатних осей х,у, z;  - частинні похідні потенціальної енергії в напрямку відповідних осей координат.
- частинні похідні потенціальної енергії в напрямку відповідних осей координат. , (3.2.10)
, (3.2.10) - оператор набла.
- оператор набла. і grad мають однаковий фізичний зміст, і відображують одну і ту ж зміну скалярної величини П в напрямку координатних осей х, у, z; тобто
і grad мають однаковий фізичний зміст, і відображують одну і ту ж зміну скалярної величини П в напрямку координатних осей х, у, z; тобто . (3.2.11)
. (3.2.11)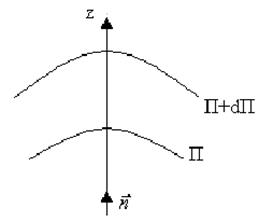

 (3.4.1)
(3.4.1)

 (3.4.2)
(3.4.2)
 . (3.4.3)
. (3.4.3) . (3.4.4)
. (3.4.4) , (3.4.5)
, (3.4.5) - повна кінетична енергія всіх тіл замкненої системи;
- повна кінетична енергія всіх тіл замкненої системи; - повна потенціальна енергія всіх матеріальних точок (тіл) замкненої системи.
- повна потенціальна енергія всіх матеріальних точок (тіл) замкненої системи.
 . (4.2.1)
. (4.2.1)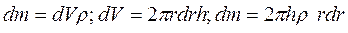 . (4.2.2)
. (4.2.2) ,
, . (4.2.3)
. (4.2.3)
 . (4.2.4)
. (4.2.4) .
.
 , помноживши попередньо весь результат на 2 (дві симетричні частини стержня)
, помноживши попередньо весь результат на 2 (дві симетричні частини стержня) . (4.2.5)
. (4.2.5) .
.
 , (4.2.6)
, (4.2.6) . (4.2.8)
. (4.2.8) [R2-z2] 2dz =
[R2-z2] 2dz =  [ R4 dz -2R2z2dz +Z4 dz ].
[ R4 dz -2R2z2dz +Z4 dz ].
 . (4.2.9)
. (4.2.9)
 (рис. 4.7).
(рис. 4.7).
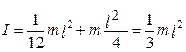 ,
, ; і t = t2 – t1. (5.2.1)
; і t = t2 – t1. (5.2.1)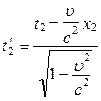 ;
;  . (5.2.2)
. (5.2.2)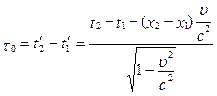 , але t2 - t1 =t, а x2 – x1 = ut,
, але t2 - t1 =t, а x2 – x1 = ut, =
= 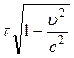 . (5.2.3)
. (5.2.3)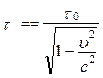 . (5.2.4)
. (5.2.4)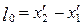 . (5.2.5)
. (5.2.5)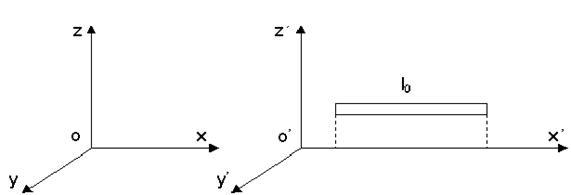
 запишемо з перетворень Лоренца для моменту часу t (в один і той же час)
запишемо з перетворень Лоренца для моменту часу t (в один і той же час)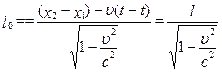 .
.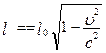 . (5.2.6)
. (5.2.6) , (5.2.7)
, (5.2.7)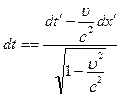 . (5.2.8)
. (5.2.8) . (5.2.9)
. (5.2.9)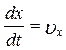 ;
; 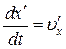 , одержимо
, одержимо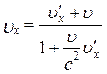 . (5.2.10)
. (5.2.10)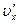 ®c, тоді швидкість цієї точки відносно спостерігача, який перебуває в стані спокою у не штрихованій системі буде дорівнювати:
®c, тоді швидкість цієї точки відносно спостерігача, який перебуває в стані спокою у не штрихованій системі буде дорівнювати: . (5.2.11)
. (5.2.11) , (5.3.1)
, (5.3.1)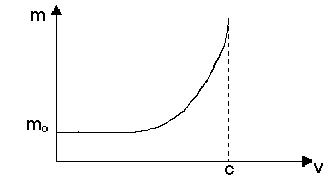

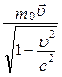 . (5.3.2)
. (5.3.2) . (5.3.3)
. (5.3.3) . (5.3.4)
. (5.3.4) , (5.3.5)
, (5.3.5) ; m0 – маса спокою цього тіла; с – швидкість світла в вакуумі.
; m0 – маса спокою цього тіла; с – швидкість світла в вакуумі.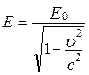 . (5.3.6)
. (5.3.6) . (5.3.7)
. (5.3.7) E2 =m2c4 = mо2с4 + p2c2. (5.3.8)
E2 =m2c4 = mо2с4 + p2c2. (5.3.8)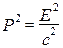 .
.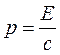 . (5.3.9)
. (5.3.9) . (6.3.2)
. (6.3.2) , тому
, тому .
. ; для a від 0 до 2p, одержимо:
; для a від 0 до 2p, одержимо:
 (6.3.3)
(6.3.3)
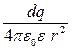 .
. . (6.3.4)
. (6.3.4) =
=  .
. .
. . (6.3.5)
. (6.3.5)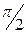 , помноживши весь вираз на 2 (враховується друга, симетрична частина нитки).
, помноживши весь вираз на 2 (враховується друга, симетрична частина нитки). .
. . (6.3.6)
. (6.3.6)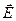 напруженості електричного поля крізь замкнену поверхню (рис. 6.9)
напруженості електричного поля крізь замкнену поверхню (рис. 6.9)
 , (6.3.7)
, (6.3.7) - величина площі заштрихованої поверхні,
- величина площі заштрихованої поверхні,  - нормаль до поверхні (одиничний вектор).
- нормаль до поверхні (одиничний вектор).
 - тілесний кут.
- тілесний кут. (тут
(тут  є тілесним кутом).
є тілесним кутом). . (6.3.8)
. (6.3.8) .
. . (6.3.9)
. (6.3.9) . (6.3.10)
. (6.3.10)
 . (6.3.11)
. (6.3.11) . (6.3.12)
. (6.3.12) .
.
 . (6.3.13)
. (6.3.13)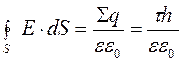 . (6.3.14)
. (6.3.14) =
=  .
. , (6.3.15)
, (6.3.15)


