Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила построения формул реляционного исчисленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В общем виде любое выражение исчисления кортежей записывается как {x(R) | f(x)}, где f – некоторый предикат над переменным кортежем х. Это выражение обозначает отношение r(R), которое состоит из тех кортежей t(R), для которых f(t) истинно. Согласно Д. Мейеру [1] основными строительными блоками для формул типа f(t) являются атомы трёх типов: 1. Если r – имя отношения из домена имён d, а х – переменный кортеж, то r(x) – атом, означающий, что x 2. Если х и у – переменные кортежи (не обязательно различные), θ 3. Если х – переменный кортеж, θ Из атомов строятся рекурсивные формулы с помощью логических связок 1. Каждый атом – формула. 2. Если f- формула, то 3. Если f и g – формулы, то f 4. Если х – переменный кортеж, f –формула, включающая x, а R - подмножество U, то 5. Если x – переменный кортеж, f – формула, включающая x, а R -подмножество U, то 6. Если f – формула, то и (f) – формула. Приоритет связок в выражениях следующий: В реляционном исчислении важными являются понятия – свободные и связанные вхождения переменной в формулу. Они несут такую же семантическую (смысловую) нагрузку, как и глобальные и локальные переменные в программе. Кванторы, т.е. связки Свободные и связанные вхождения переменных определяются рекурсивно одновременно с type (x,f) - типом переменной x в формуле f и men(x,f) – множеством ссылок переменной x в f. И тип переменной type (x,f), и множество ссылок men(x,f) определены только в случае, если x имеет свободное вхождение в f (т.е. «x появляется в f свободно). Понятия свободы, связанности, типа и множества ссылок используются для определения класса разрешённых формул через ограничения на употребление различных связок. Случай, когда f – атомарная формула: § если f = r(x), то x свободно в f, а type (x,f) = men(x,f) =R, где R – схема отношения r. § если f = x(A) θ y(B), то х и у свободны в f, type (x,f) и type (у,f) не определены, а men(x,f) =А, men(у,f) = В. § если f = x(A) θ с или f = с θ x(A), то х свободна в f, type (x,f) не опреде лён, а men(x,f) = А. Атомарные формулы всегда разрешены, если удовлетворяют требованиям на домены и знаки сравнения. Случай, когда f строится из меньших формул, предполагая, что g и h – разрешённые формулы: · если f = · если f = f · если f = · если f = (g), то f разрешена, а свободные вхождения, связанные вхождения, тип и множество ссылок переменных остаются теми же, что и у g. В формулах вида Квантор существования Квантор (quantum-сколько, лат.) – это оператор, формализующий в исчислении предикатов их логические свойства и, в целом, обозначает количество чего-либо. Квантор существования означает, что существует хотя бы один экземпляр определённого типа объектов и в реляционном исчислении используется для задания условия того, что определённый тип строк в отношении существует. Он реализуется оператором EXISTS… IN. Пример 3.13: БД авторемонтного цеха состоит из отношений СБОРКА и ДЕТАЛИ (рис. 3.1). Отношение СБОРКА содержит данные о деталях, необходимых для сборки автомобиля и их требуемом количестве, отношение ДЕТАЛИ – о наличии деталей и их общем количестве. Требуется определить названия деталей, обеспечивающих потребности сборочного процесса. СБОРКА ДЕТАЛИ
Запрос: Определить перечень деталей, имеющихся в достаточном количестве для сборки автомобиля. Решением будет отношение, состоящее из одного столбца и содержащее названия деталей. Если t – строка отношения СБОРКА, а s – строка отношения ДЕТАЛИ, то полное решение в реляционном исчислении, состоящее из целевого списка и определяющего выражения примет вид: { t.Hазв_дет | t IN СБОРКА AND EXISTS s IN ДЕТАЛИ (s.Код_дет = t.Клд_дет AND s. Код-во > t.Кол-во)}. В развёрнутом виде оно читается, как «Поместить в отношение решения строку t атрибута Назв_дет из отношения СБОРКА, если существует строка s в отношении ДЕТАЛИ такая, что значение атрибута Код_дет строки s из ДЕТАЛИ равно значению атрибута Код_дет строки t из СБОРКА и значение атрибута Кол-во строки s больше значения атрибута Кол-во строки t». Действие квантора существенности в решении выражается оператором exists s IN, в котором описывается условие существования описанных в запросе строк отношений. Алгоритм обработки таблиц БД этим выражением аналогичен рассмотренному в п. 3.2.1. для примера 3.11 (последовательный просмотр строк отношений с проверкой для каждого сочетания строк условий определяющего выражения на истинность). В итоге получим результирующее отношение вида:
В реляционной алгебре для выполнения этого запроса требуется операция «Соединение Join». В примере 2.13 показано использование квантора существенности в реляционном исчислении для выполнения функции соединения.
Квантор всеобщности Квантор всеобщности означает, что условие полной записи решения запроса применяется в отношениях БД ко всем или к каждой строке некоторого типа и реализуется оператором FORALL (для всех - англ.). Он соответствует операции деления реляционной алгебры. Рассмотрим его применение в запросе к таблицам БД (пример 3.13). Пример 3.14. Даны отношения: БД: r МНОГОБОРЦЫ р вИДЫ СПОРТА
Определить фамилии спортсменов, участвовавших во всех видах соревнований из отношения вИДЫ СПОРТА. Условие выбора спортсмена содержит слово каждый вид спорта, поэтому в полном решении целесообразно использование квантора FORALL: {t.Фамилия | t IN МНОГОБОРЦЫ AND s IN вИДЫ СПОРТА AND FORALL s (t. Вид_спорта = s. Вид_спорта)} где t - кортеж отношения МНОГОБОРЦЫ; S – кортеж отношения вИДЫ СПОРТА. Результирующее отношение примет вид:
В нём записан спортсмен Панов, поскольку он присутствует в строках t1 и t 2 причём t1 соответствует s1 и s2, и t2 соответствует s1 и s2, т.е. перебирается каждое сочета ние атрибутов строк t и s. По этой же причине в отношении решения присутствует Рогов, а Селина в отношении нет, поскольку он присутствует только в строке t5, которая соответствует строке s1, но не соответствует строке s2. Таким образом, полное соответствие всем строкам отношения вИДЫ СПОРТА есть только у спортсменов Панов и Рогов.
ЛЕКЦИЯ 11 ТЕМА: ОСНОВЫ ФРАКТАЛОВ. ПЛАН
1Типы фракталов 2 Фрактальные методы в архивации 3 Сжатие данных
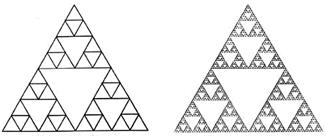
Типы фракталов Всё множество фракталов можно разделить на три основные группы: · геометрические (конструктивные) фракталы; · алгебраические (динамические) фракталы и · стохастические фракталы. Геометрические фракталы являются самыми наглядными. Их получают с помощью генератора в виде некоторой ломаной в двумерной топологии или в виде поверхности в трехмерном случае. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал. Типичные конструктивные фракталы показаны на рис. 4.1-4.7.
Образующим элементом является Т-образный элемент, который на каждом шаге уменьшается вдвое и присоеди-няется к концам ветви предыдущего поколения, показатель уменьшения 1/2 Рис. 4.1 Двоичное дерево (дендрит)
Рис. 4.2 Кривая Кох и её вариант – «снежинка» Кох Знаменитая кривая Кох придумана Хельгой фон Кох в 1904 г. – на основе средней трети строится равносторонний треугольник, процесс также бесконечно повторяется, сумма отрезков в пределе равна бесконечности, фрактальная размерность: lg 4/lg3 = 1,2618…. Это пример кривой, которая нигде не имеет касательной. Она состоит из частей, каждая из которых имеет бесконечную длину. Построение квадратов на сторонах правильного пятиугольника дает в сумме подобный ему пятиугольник больших размеров:
Рис. 4.3 Пятиугольник Альбрехта Дюрера (начало 16 в.) Кантор (1845-1918) - один из основателей теории множеств. Топологическая размерность конструкции фрактала равна 0 (т.к. общая длина всех отрезков в пределе равна 0), показатель уменьшения составляет 1/3, а фрактальная размерность– 0,6309…
Рис. 4.4 Конструкция фрактала Кантора
Рис. 4.5 Гребень Кантора Гребень Кантора(1883 г.) выполнен на основе удаления средней трети отрезка – повторение подобной операции до бесконечности ведет к образованию так.называемой канторовской пыли, длина которой в сумме равна 0.
Рис. 4.6 Схема решета Серпинского и Решето Серпинского Решето Серпинского (1915) (Вацлав Серпинский – польский математик) построено на основе равностороннего треугольника.
Рис. 4.7 Кривая дракона (автор – Дж. Хайвер) Кривая дракона – это ломаная линия, нигде не пересекает саму себя, постепенно заполняющая плоскость. Алгебраические (динамические) фракталы - самая крупная группа фракталов.. Одним из первых их описал французский математик Гастон Жюлиа в 1918 году. Примерами фрактальной структуры в природе являются линия морского берега, многие естественные границы, которые становятся явно тем длиннее, чем более мелкий масштаб используется для их измерения. Границы такого рода в математике и называют множествами Жулиа (Julia). Динамические фракталывозникают в нелинейных динамических системах, в первую очередь – в дискретных. Их построение сложнее, чем у конструктивных фракталов, и самоподобность в них может проявляться только приближённо. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Нелинейные динамические системы обладают несколькими устойчивыми состояниями (аттракторами). То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. При этом можно с помощью несложных алгоритмов порождать очень сложные нетривиальные структуры (рис. 4.8).
Рис. 4.8 Алгебраический фрактал Исследования Мандельброта состояли в обобщении множеств Жюлиа-Фату. Множество Жулиа-Фату – это множество с обратной связью, когда следующее значение функции вычисляется на основе предыдущего: xn+1 = f(xn), но при этом существует нелинейная зависимость между результатами функции – например, в виде xn+1 = xn2 + c).
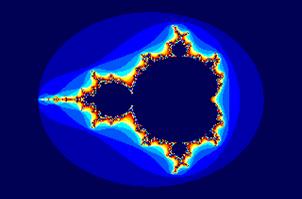
Рис. 4.9 Множества Жюлиа При определенных начальных условиях значение функции быстро стабилизируется на каком-то одном значении (аттракторе), а в других случаях – уходит в бесконечный хаос. Наибольший интерес представляла граница перехода функции от порядка к хаосу. На рис. 4.9. показаны множества Жюлиа (очертания границ фазового перехода на комплексной плоскости) Мандельброт также построил универсальное множество, описывающее свойства фазового перехода для всех множеств Жюлиа вида x=x2 + c (рис. 4.10).
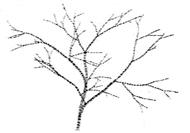
Рис. 4.10 Множество Мандельброта (Mandelbrot) Стохастические фракталы получаются, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты, очень похожие на природные - несимметричные деревья, скалы, изрезанные береговые линии и др. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
Рис. 4.8 Стохастический фрактальный дендрит и мистический лес Ввод случайного возмущения в регулярный математический древовид ный фрактал(дендрит – рис. 4.1) позволяет добиться сходства с настоящим деревом (рис.4.8) В настоящее время фракталы используются в ряде прикладных областей: динамическое моделирование (и их графическое отображение) различных процессов - турбулентности в жидкостях, колебаний в электросетях и химических средах, множество биологических процессов и др. В музыке (припев в песне – типичный фрактальный элемент) приложение элементов фрактальной геометрии используются в трех основных областях: композиция, синтез звука и аналитические исследования. Основными свойствами фрактальных множеств (F) являются: 1. Тонкая структура, т.е. F содержит произвольно малые масштабы и допускается бесконечное увеличение. 2. Нерегулярность, т.е. F не может быть описано на традиционном геометрическом языке. 3. F имеет некоторою форму самоподобия, статистическую – для крнструктивных и приближённую – для алгебраических, но в целом каждый уровень подобен всему F. 4. F множества имеют свою, «фрактальную размерность», большую, чем его топологическая размерность 5. F теоретически многомерно, т.е. можно изменять его в любом количестве измерений. 6. Простота определения F, чаще всего – рекурсивно
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-27; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.188.105 (0.015 с.) |

 r.
r. (НЕ),
(НЕ),  (И),
(И),  (ИЛИ),
(ИЛИ),  (Существует) и
(Существует) и 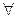 (для каждого). Построение выражений производится по шести правилам:
(для каждого). Построение выражений производится по шести правилам: f – формула.
f – формула. или
или  и
и  men(x,h). В обоих случаях type (x,f) = type (x,g). Если тип х не определён в обеих подформулах, то type (x, f) не определён. В любом случае men(x,f) = men(x, g) U men(x, h).
men(x,h). В обоих случаях type (x,f) = type (x,g). Если тип х не определён в обеих подформулах, то type (x, f) не определён. В любом случае men(x,f) = men(x, g) U men(x, h).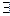 x(R) g или f =
x(R) g или f =  Эта конструкция (дендрит – от dendron - греч. – дерево) имеет сходство с двоичной системой счисления.
Эта конструкция (дендрит – от dendron - греч. – дерево) имеет сходство с двоичной системой счисления.