
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление функции нескольких переменныхСодержание книги
Поиск на нашем сайте
14. Дайте определение расстояния 15. Дайте определение открытого множества в 16. Дайте определение замкнутого множества в 17. Дайте определение открытого множества в 18. Дайте определение предельной точки множества. Приведите примеры: а) множества, содержащего все свои предельные точки, б) множества, для которого существует предельная точка, ему не принадлежащая. 19. Дайте определение сходящейся последовательности точек в 20. Дайте определение сходящейся последовательности точек в 21. Дайте определение предела функции двух переменных в точке. Найдите предел функции 22. Дайте определение предела функции двух переменных в точке. Докажите, что функция 23. Дайте определение функции двух переменных, непрерывной в точке. Является ли функция 24. Докажите, что функция 25. Дайте определение частной производной функции 26. Дайте определение частных производных функции 27. Дайте определение дифференцируемости функции 28. Дайте определение дифференциала функции 29. Как связаны производная по направлению и градиент дифференцируемой функции 30. Дайте определение градиента функции 31. Дайте определение однородной функции степени 32. Дайте определение однородной функции нескольких переменных. Приведите пример однородной функции 33. Дайте определение однородной функции степени 34. Дайте определение локального экстремума функции двух переменных. Является ли равенство нулю частных производных функции в некоторой точке достаточным условием ее локального экстремума в этой точке? 35. Дайте определение локального экстремума функции двух переменных. Имеет ли функция 36. Дайте определение локального экстремума функции двух переменных. Имеет ли функция 37. Сформулируйте достаточное условие локального экстремума функции двух переменных. Имеет ли функция 38. Докажите, что функция 39. Найдите наименьшее значение функции 40. Рассмотрев линии уровня функции
Интегральное исчисление функций нескольких переменных
41. Вычислите интеграл от функции 42. Докажите, что 43. Сформулируйте теорему о замене переменных в двойном интеграле. Вычислите интеграл, перейдя к полярным координатам, Ряды
44. Дайте определение числового ряда и его суммы. Найдите, исходя из определения, сумму ряда 45. Дайте определения числового ряда и его суммы. Исходя из определения докажите, что сумма ряда 46. Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример расходящегося ряда, для которого это условие выполнено. 47. Докажите, что если ряд 48. Докажите, что для сходимости ряда 49. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами. 50. Сформулируйте признак Даламбера в предельной форме для числовых рядов с положительными членами. Приведите пример сходящегося ряда с положительными членами, к которому этот признак не применим. 51. Сформулируйте признаки сравнения для числовых рядов с неотрицательными членами. Используя этот признак, докажите, что ряд 52. Сформулируйте интегральный признак сходимости числового ряда с положительными членами. При каких положительных значениях 53. Какой числовой ряд называется гармоническим? Докажите, что гармонический ряд расходится. 54. Сформулируйте признак Лейбница для знакочередующихся числовых рядов. Приведите пример знакочередующегося ряда, сходящегося условно.
Примеры задач 1.Интегральное исчислениефункции одной переменной Найти интеграл: 1.1. 1.3. 1.5. 1.7. 1.9. 1.11. 1.13. 1.15. 1.17. 1.19.
Найти несобственный интеграл: 1.21. 1.23. 1.25. Найти площадь фигуры, ограниченной линиями: 1.27. 1.28. 1.29. 1.30. 1.31. Найти объем тела, образованного вращением вокруг оси 1.32. 1.33. 2.Дифференциальное исчисление функции нескольких переменных Найдите первый и второй дифференциалы функции 2.1. 2.2. 2.3. 2.4. 2.5.
2.6. Найдите производную функции 2.7. Найдите производную функции 2.8. Найдите производную функции 2.9. Найдите производную функции 2.10. Найдите производную функции 2.11. Найдите производную функции 2.12. Найдите производную функции
Найдите точки локального экстремума функции: 2.13. 2.14. 2.15. 2.16. 2.17. 2.18. 2.19. Найдите наибольшее и наименьшее значения функции 2.20. 2.21. 2.22. 2.23. 2.24.
Найти условные экстремумы функции: 2.25. 2.26.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 296; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.93 (0.006 с.) |

 между точками
между точками  . Сформулируйте и докажите свойства функции
. Сформулируйте и докажите свойства функции  . Является ли множество
. Является ли множество  открытым? Ответ обоснуйте.
открытым? Ответ обоснуйте. замкнутым? Ответ обоснуйте.
замкнутым? Ответ обоснуйте. открытым? Ответ обоснуйте.
открытым? Ответ обоснуйте. . К какой точке в
. К какой точке в  ? Ответ обоснуйте.
? Ответ обоснуйте. . К какой точке в
. К какой точке в  ? Ответ обоснуйте.
? Ответ обоснуйте. в точке
в точке  . Ответ обоснуйте.
. Ответ обоснуйте. не имеет предела в точке
не имеет предела в точке  .
. непрерывной в точке
непрерывной в точке  непрерывна в точке
непрерывна в точке  .
. по
по  в точке
в точке  . Найдите
. Найдите  , если
, если  .
. в точке
в точке  .
. . Является ли функция
. Является ли функция  однородной? Если да, то какой степени?
однородной? Если да, то какой степени? локальный экстремум в точке
локальный экстремум в точке  локальный экстремум в точке
локальный экстремум в точке  в точке
в точке  : а) не имеет локального экстремума в точке
: а) не имеет локального экстремума в точке 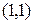 , б) имеет в этой точке условный локальный экстремум при наличии связи
, б) имеет в этой точке условный локальный экстремум при наличии связи  .
. .
. она принимает наибольшее и наименьшее значения, найти эти значения.
она принимает наибольшее и наименьшее значения, найти эти значения. по области D, ограниченной прямыми
по области D, ограниченной прямыми  ,
,  и параболой
и параболой  .
. , где
, где  .
. , где
, где  .
. при
при  .
. равна числу 1.
равна числу 1.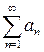 сходится, а ряд
сходится, а ряд  расходится, то ряд
расходится, то ряд  расходится.
расходится. , необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.
, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена. расходится.
расходится. сходится, а при каких расходится? Ответ обоснуйте.
сходится, а при каких расходится? Ответ обоснуйте. 1.2.
1.2. 
 . 1.4.
. 1.4.  .
. . 1.6.
. 1.6.  .
.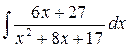 . 1.8.
. 1.8. 
 . 1.10.
. 1.10. 
 . 1.12.
. 1.12.  .
. . 1.14.
. 1.14.  .
. . 1.16.
. 1.16. 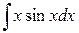 .
. . 1.18.
. 1.18.  .
. . 1.20.
. 1.20.  .
.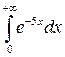 . 1.22.
. 1.22.  .
. . 1.24.
. 1.24.  .
. . 1.26.
. 1.26.  .
.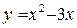 и
и  .
. и
и  .
. и
и  .
. и
и  .
. ,
,  и
и  плоской фигуры, ограниченной линиями:
плоской фигуры, ограниченной линиями: и
и  .
. ,
,  и
и  .
.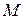 :
: в точке
в точке  .
. в точке
в точке  .
.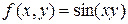 в точке
в точке  .
. в точке
в точке  .
. в точке
в точке  .
. в точке
в точке 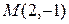 по направлению, составляющему угол
по направлению, составляющему угол  с осью
с осью  .
. в точке
в точке  по направлению вектора
по направлению вектора 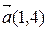 .
. в точке
в точке  по направлению, составляющему угол
по направлению, составляющему угол  в точке
в точке  по направлению, составляющему угол
по направлению, составляющему угол  в точке
в точке 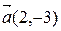 .
. в точке
в точке  по направлению, составляющему угол
по направлению, составляющему угол  в точке
в точке  по направлению вектора
по направлению вектора  .
. .
. .
. .
.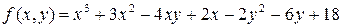 .
.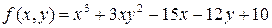
 .
. .
. :
: ,
,  .
. ,
,  .
. ,
,  .
. ,
,  с вершинами
с вершинами 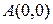 ,
,  ,
,  .
.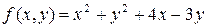 ,
,  .
. при
при  .
. при
при  .
.


