
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика расчета зачетных балловСодержание книги
Поиск на нашем сайте
Письменный зачет (максимум 80 баллов) + работа в триместре (максимум 20 баллов).
80-балльная оценка за письменный зачет получается суммированием оценок за ответ на каждый вопрос зачета. 20-балльная оценка за работу в триместре складывается из 10-балльной оценки за первую половину триместра и 10-балльной оценки за вторую половину триместра. 10-балльная оценка за половину триместра получается преобразованием 100-балльной оценки по следующей таблице:
III. СОДЕРЖАНИЕ ЗАЧЕТА Теоретические вопросы (А) (определения, свойства и теоремы на уровне формулировок) 1. Определение первообразной для функции 2. Определение неопределенного интеграла. 3. Свойства неопределенного интеграла. 4. Таблица основных интегралов. 5. Формула замены переменной в неопределенном интеграле. 6. Формула интегрирования по частям для неопределенного интеграла. 7. Определение определенного интеграла Римана. 8. Достаточное условие интегрируемости. 9. Геометрический смысл определенного интеграла. 10. Свойства определенного интеграла. 11. Формула Ньютона-Лейбница. 12. Формула замены переменной в определенном интеграле. 13. Формула интегрирования по частям для определенного интеграла. 14. Определение несобственного интеграла с бесконечным верхним пределом. 15. Определение несобственного интеграла с бесконечным нижним пределом. 16. Определение несобственного интеграла от неограниченной функции на ограниченном промежутке. 17. Пространство 18. Расстояние в 19. Окрестность точки в 20. Внутренние и граничные точки множества. 21. Открытые и замкнутые множества. 22. Изолированные и предельные точки множества. 23. Ограниченные множества. 24. Сходимость последовательности точек в 25. Функция нескольких переменных. 26. Поверхности (линии) уровня функции нескольких переменных. 27. Предел функции нескольких переменных. 28. Непрерывность функции нескольких переменных. 29. Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значений. 30. Частные производные функции нескольких переменных. 31. Дифференцируемость функции нескольких переменных. 32. Дифференциал функции нескольких переменных. 33. Достаточное условие дифференцируемости функции нескольких переменных. 34. Непрерывность дифференцируемой функции. 35. Производная сложной функции. 36. Производная по направлению. 37. Градиент. Свойства градиента. 38. Эластичность функции нескольких переменных. 39. Однородные функции. 40. Формула Эйлера для однородной функции. 41. Частные производные высших порядков. 42. Теорема о равенстве смешанных производных. 43. Локальные экстремумы функций нескольких переменных. 44. Необходимое условие локального экстремума функций нескольких переменных. 45. Достаточное условие локального экстремума функций нескольких переменных. 46. Условный экстремум. 47. Метод Лагранжа. 48. Наибольшее и наименьшее значения непрерывной функции на замкнутом ограниченном множестве. 49. Кратные интегралы и их свойства. Условия интегрируемости функции. 50. Сведение кратного интеграла к повторному интегралу. 51. Формула замены переменных в двойном интеграле. Использование полярных координат для вычисления двойных интегралов. 52. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур и объемов пространственных тел. 53. Несобственные кратные интегралы. Интеграл Эйлера-Пуассона. 54. Числовые ряды. 55. Последовательность частичных сумм. Сумма ряда. Сходящиеся ряды. 56. Свойства сходящихся рядов. 57. Необходимое условие сходимости числового ряда. 58. Числовые ряды с неотрицательными членами. 59. Критерий сходимости числовых рядов с неотрицательными членами. 60. Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами. 61. Знакопеременные ряды. Абсолютная и условная сходимость. 62. Признак Лейбница для знакочередующихся числовых рядов. Теоретические вопросы (Б) Интегральное исчисление 1. Докажите, что если 2. Докажите, что 3. Докажите формулу интегрирования по частям для неопределенного интеграла. 4. Докажите формулу замены переменной для неопределенного интеграла. 5. Докажите, что если функция 6. Используя свойство интеграла с переменным верхним пределом, докажите формулу Ньютона-Лейбница. 7. Применив замену переменной в определенном интеграле, докажите, что для любой четной непрерывной на отрезке 8. Применив замену переменной в определенном интеграле, докажите, что для любой нечетной непрерывной на отрезке 9. Сходится ли интеграл 10. Сходится ли интеграл 11. При каких значениях 12. Сходится ли интеграл 13. При каких значениях
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.115.187 (0.006 с.) |

 на промежутке
на промежутке 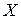 .
. .
. и
и  – первообразные функции
– первообразные функции  на интервале
на интервале  , то
, то 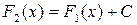 , где
, где  – некоторая постоянная.
– некоторая постоянная.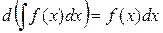 .
. , то функция
, то функция 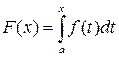 ,
,  , является ее первообразной на этом отрезке.
, является ее первообразной на этом отрезке. функции
функции 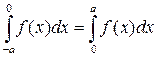 . В чем состоит его геометрический смысл?
. В чем состоит его геометрический смысл?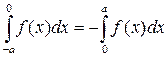 . В чем состоит его геометрический смысл?
. В чем состоит его геометрический смысл? ? Ответ обоснуйте.
? Ответ обоснуйте. ? Ответ обоснуйте.
? Ответ обоснуйте. сходится интеграл
сходится интеграл  ? Ответ обоснуйте.
? Ответ обоснуйте. ? Ответ обоснуйте.
? Ответ обоснуйте. сходится интеграл
сходится интеграл  ? Ответ обоснуйте.
? Ответ обоснуйте.


