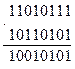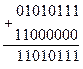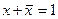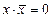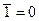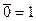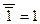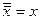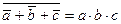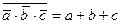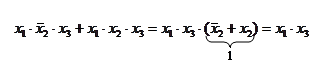Глава 6. Комбинационные цифровые схемы

Комбинационными цифровыми схемами называют схемы, выходные сигналы которых зависит только от сигналов, поданных на их входы в данный момент, и не зависят от состояния схемы в предыдущий момент времени. К комбинационным схемам обычно относят такие микросхемы, как дешифраторы, шифраторы, мультиплексоры и демультиплексоры.

Создание цифровых комбинационных устройств в настоящий момент в значительной степени формализовано, при этом для создания их принципиальных схем могут оказаться полезны некоторые законы алгебры логики. Несмотря на то, что все эти законы получены из таблиц истинности простейших логических элементов, применение этих законов оказывается более удобным при создании принципиальной схемы цифрового устройства.

Законы алгебры логики

Законы алгебры логики базируются на аксиомах и позволяют преобразовывать логические функции. Логические функции преобразуются с целью их упрощения, что приводит к упрощению схемы цифрового устройства.

АКСИОМЫ алгебры логики описывают действие логических функций "И" и "ИЛИ" и записываются следующими выражениями:

функция "И" функция "ИЛИ"

0 × 0 = 0 0 + 0 = 0

0 × 1 = 0 0 + 1 = 1

1 × 0 = 0 1 + 0 = 1

1 × 1 = 1 1 + 1 = 1

В данных выражениях знак ‘×’ используется для обозначения операции логического умножения, а знак ‘+’ — для обозначения операции логического суммирования. Всего при разработке цифровых комбинационных устройств используется пять законов алгебры логики:

Закон одинарных элементов.

1 × X = X

0 × X = 0

1 + X = 1

0 + X = X

Этот закон непосредственно следует из приведенных выше выражений аксиом алгебры логики (таблицы истинности логических элементов). Верхние два выражения могут быть полезны при построении коммутаторов, ведь подавая на один из входов элемента "2И" логический ноль или единицу можно либо пропускать сигнал на выход, либо формировать на выходе нулевой потенциал.

Второй вариант использования этих выражений заключается в возможности избирательного обнуления определенных разрядов многоразрядного числа. При поразрядном применении операции "И" можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды единичный или нулевой потенциал. Например, в восьмиразрядном двоичном числе требуется обнулить 6, 3 и 1 разряды. Тогда, при выполнении операции поразрядного логического умножения получим:

В приведенном примере отчетливо видно, что для обнуления необходимых разрядов в маске (нижнее число) на месте соответствующих разрядов записаны нули (не забываем, что счет начинается с нулевого разряда), в остальных разрядах записаны единицы. В исходном числе (верхнее число) на месте 6 и 1 разрядов находятся единицы. После выполнения операции "И" на этих местах появляются нули. На месте третьего разряда в исходном числе находится ноль. В результирующем числе на этом месте тоже присутствует ноль. Остальные разряды исходного числа, как и требовалось по условию задачи, не изменены.

Записывать логические единицы в нужные нам разряды многоразрядного двоичного числа можно точно таким же образом. В этом случае необходимо воспользоваться нижними двумя выражениями закона одинарных элементов. При поразрядном применении операции "ИЛИ" можно либо оставлять прежнее значение разряда, либо заносить в него единичное значение, подавая на соответствующие разряды нулевой или единичный потенциал. Пусть требуется записать единицы в 7 и 6 биты восьмиразрядного числа.

Тогда, при выполнении операции поразрядного логического суммирования исходного числа с маской устанавливаемых бит, получим:

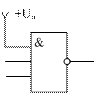
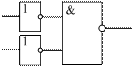
Здесь в маску (нижнее число) мы записали единицы в седьмой и шестой биты. Остальные биты содержат нули, и, следовательно, не могут изменить первоначальное состояние исходного числа, что мы и видим в соответствующих разрядах результирующего числа под чертой.

Первое и последнее выражения закона одинарных элементов позволяют использовать логические элементы с большим количеством входов в качестве элементов с меньшим количеством входов, если в схеме уже есть такие свободные элементы и не хочется вводить в состав принципиальной схемы дополнительные микросхемы. Для этого неиспользуемые входы логического элемента "И" должны быть подключены к источнику питания, как это показано на рис. 6.1.

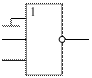
Рис. 6.1. Схема "2И-НЕ", реализованная на элементе "3И-НЕ"

В схеме логического элемента "ИЛИ", согласно закону одинарных элементов, для уменьшения количества входов логического элемента, неиспользуемые входы должны быть подключены к общему проводу схемы, как это показано на рис. 6.2.

Рис. 6.2. Схема"2ИЛИ-НЕ", реализованная на элементе "3ИЛИ-НЕ"

Законы отрицания.

q Закон дополнительных элементов:

q Двойное отрицание:

Выражения, примененные в этих законах, широко используется для минимизации логических схем. Если удается выделить из общего выражения логической функции цифрового комбинационного устройства такие подвыражения, то можно сократить необходимое количество входов логических элементов в составе цифровой схемы, а иногда и вообще свести все выражение к логической константе.

q Закон отрицательной логики:

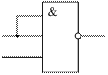
Закон отрицательной логики справедлив для любого числа переменных. Этот закон позволяет реализовывать логическую функцию "И" при помощи логических элементов "ИЛИ" и наоборот: реализовывать логическую функцию "ИЛИ" при помощи логических элементов "И". Это особенно полезно в ТТЛ схемотехнике, так как там легко реализовать логические элементы "И", но при этом достаточно сложно реализуются логические элементы "ИЛИ". Благодаря закону отрицательной логики можно достаточно просто реализовывать элементы "ИЛИ" на логических элементах "И". На рис. 6.3 показана реализация логического элемента "2ИЛИ" на элементе "2И-НЕ" и двух инверторах.

Рис. 6.3. Логический элемент "2ИЛИ", реализованный на элементе "2И-НЕ"

То же самое можно сказать и о схеме монтажного "ИЛИ". В случае необходимости его можно превратить в монтажное "И", применив инверторы на входе и выходе этой схемы.

Комбинационные законы.

При применении комбинационных законов можно значительно упростить логическое выражение, описывающее цифровую схему и, тем самым, упростить ее принципиальную схему. Это позволяет сократить занимаемую цифровой схемой площадь на кристалле и потребляемый ею ток. Комбинационные законы алгебры логики во многом соответствуют комбинационным законам обычной алгебры, но есть и отличия.

q Закон тавтологии (многократное повторение):

x × x × x × x = x

x + x + x + x = x

Применение этого закона зависит от цели. Его можно использовать для минимизации схемы, если такое выражение получается в результате преобразований исходного логического выражения.

Этот же закон позволяет использовать логические элементы с большим количеством входов в качестве элементов с меньшим количеством входов. Например, можно реализовать двухвходовую схему "2И" на элементе "3И", как это показано на рис. 6.4. или использовать схему "2И‑НЕ" в качестве обычного инвертора, как это показано на рис. 6.5.

Рис. 6.4. Схема "2И-НЕ", реализованная на элементе "3И-НЕ"

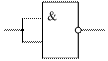
Рис. 6.5. Схема "НЕ", реализованная на элементе "2И-НЕ"

Однако следует предупредить, что объединение нескольких входов увеличивает входные токи логического элемента и его входную емкость, что увеличивает ток потребления предыдущих элементов и отрицательно сказывается на быстродействии цифровой схемы в целом. Для уменьшения числа входов в логическом элементе лучше воспользоваться законом одинарных элементов, как это было показано выше.

q Закон переместительности.

a + b + c + d = a + c + b + d

В случае применения этого закона можно сократить площадь печатной платы за счет того, что в ряде случаев можно одни выводы логического элемента заменить на другие. В результате при разработке конструкции цифрового устройства можно избежать переходов проводника на другой слой печатной платы или сократить общую длину проводников.

q Закон сочетательности.

a + b + c + d = a + (b + c) + d = a + b + (c + d)

Этот закон позволяет составлять многовходовые логические элементы из логических элементов с меньшим количеством входов. Причем комбинации элементов могут быть самыми разнообразными

q Закон распределительности.

х₁×(х₂ + х₃) = х₁×х₂ + х₁×х₃

х₁ + х₂×х₃ =(х₁+х₂)×(х₁+х₃)

Докажем это выражение путем раскрытия скобок в правой части равенства:

(х₁+х₂) (х₁+х₃)=х₁х₁+х₁х₃+х₁х₂+х₂ х₃== х₁ (1+ х₃ + х₂)+ х₂х₃ = х₁+х₂х₃

13. Правило поглощения.

х₁ + х₁×х₂×х₃ = х₁×(1 + х₂×х₃) = х₁

Одна переменная (в данном случае логическая переменная x₁) поглощает другие.

14. Правило склеивания.

Обратите внимание, что это правило выполняется только по одной переменной.

Также как в обычной математике, в алгебре логики имеется старшинство операций. При выполнении логических выражений первым выполняется:

1. Действие в скобках.

2. Операция с одним операндом (одноместная операция) — "НЕ".

3. Конъюнкция — "И".

4. Дизъюнкция — "ИЛИ".

5. Сумма по модулю два.

Операции одного ранга выполняются слева направо в порядке написания логического выражения. Алгебра логики линейна и для нее справедлив принцип суперпозиции.