Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условные законы распределения составляющих системы
непрерывных случайных величин. Пусть (Х,У) непрерывная двумерная случайная величина. Условной плотностью вероятности одной из одномерных составляющих двумерной случайной величины называется отношение ее совместной плотности к плотности вероятности другой составляющей, т.е.
Эти соотношения, записанные в виде
называются теоремой (правилом) умножения плотностей распределения. Отличие, например, условной плотности f(x/y) от безусловной плотности f(x) состоит в том, что функция f(x/y) дает распределение Х при условии, что составляющая У приняла значение У = у, а функция f(x) дает распределение Х независимо от того, какие из возможных значений приняла составляющая У. Если известна плотность совместного распределения f(x,y), то условные плотности составляющих могут быть найдены по формулам
Как и любая плотность распределения, условные плотности обладают следующими свойствами
Условное математическое ожидание. Условным математическим ожиданием дискретной случайной величины У при Х = х называется произведение возможных значений У на их условные вероятности, т.е.
Для непрерывных величин
где f(y/x) условная плотность случайной величины У при Х = х. Если M(Y/(X = x)) меняется в зависимости от х, то говорят о регрессионной зависимости У на Х, при этом сама эта зависимость называется регрессией У на Х. Аналогично определяются условное математическое ожидание случайной величины Х и регрессия Х на У. Пример. Дискретная двумерная случайная величина задана таблицей
Найти условное математическое ожидание У при Х = х1, где х1 = 1. ▼ р(х1) = 0,15 + 0,30 = 0,45. Найдем условные распределения вероятностей У при Х = х1
Тогда
Зависимые и независимые случайные величины. Две случайные величины независимы, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых величин равны их безусловные распределения Условие независимости случайных величин Х, У, рассматриваемых совместно, заключается в выполнении следующих равенств:
Или для вероятностей:
Из соотношения для вероятностей можно дать следующее определение независимых дискретных случайных величин. Дискретные случайные величины Х, У называются независимыми, если Дадим общее определение независимости случайных величин. Случайные величины Х, У называются независимыми, если их совместная функция распределения F(x,y) равна произведению функций распределения составляющих, т.е.
Следствие. Непрерывные случайные величины Х, У являются независимыми, если их совместная плотность распределения равна произведению плотности распределения составляющих, т.е.
В общем случае две случайные величины могут быть независимыми, функционально зависимыми и статистически (вероятностно) зависимы. Функциональная зависимость между Х, У задается в виде точной формулы, в которой каждому значению одной переменной соответствует строго определенное значение другой. Статистическая (вероятностная) зависимость между Х, У задается в виде, когда каждому значению одной из них соответствует определенное (условное) распределение другой. Если М(У/(X = x)) изменяется при изменении х, то статистическая зависимость М(У/x) = g(x) называется функцией регрессии У на Х.
Ковариация и коэффициент корреляции. Ковариацией случайных величин Х, У называется математическое ожидание произведения отклонений этих величин от своих средних, т.е.
Для дискретных случайных величин или Для непрерывных случайных величин
Заметим, что cov(X,X) = D(X), cov(Y,Y) = D(Y). Пример. Закон распределения дискретной двумерной случайной величины задан таблицей
Найти ковариацию случайных величин Х, У. ▼ μx = M(X) = ΣΣxipij = 1∙(0,35 + 0,30 + 0,15) + 2∙(0,05 + 0,10 + 0,05) =1,2; μy = M(Y) = ΣΣyjpij = 1∙(0,30 + 0,10) + 2∙(0,15 + 0,05) =0,8; M(XY) = ΣΣxiyjpij = 1∙1∙0,30 + 1∙2∙0,15 + 2∙1∙0,10 + 2∙2∙0,05 = 1,0; с ov(X,Y) = M(XY) – μxμy = 1,0 – 1,2∙0,8 = 0,04.
Свойства ковариации. 1. Ковариация двух независимых случайных величин равна нулю, т.е. если Х,У независимы, то с ov(X,Y) = 0.
2. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений
Ковариация служит для характеристики связи между величинами Х,У. Если ковариация не равна нулю, то Х, У – зависимы. Ковариация – размерная величина, что затрудняет ее использование для оценки степени зависимости различных случайных величин. Чтобы устранить этот недостаток, вводят новую числовую характеристике - коэффициент корреляции. Коэффициентом корреляции двух случайных величин называется отношение их корреляции к произведению средних квадратических отклонений этих величин, т.е.
Коэффициент корреляции является безразмерной величиной, изменяющийся в пределах -1 ≤ ρ ≤ 1. Коэффициент корреляции показывает степень (тесноту) линейной связи двух случайных величин, причем: r> 0 при положительной связи и r = 1 при строгой положительной линейной связи; r < 0 при отрицательной связи и r = -1 при строгой отрицательной линейной связи; r = 0 при отсутствии линейной связи. Случайные величины X, Y называются некоррелированными, если r =0, и коррелированными, если r Независимость случайных величин X, Y означает отсутствие любой связи (линейной и нелинейной), а некоррелированность – отсутствие только линейной связи. Свойство. Если случайные величины X, Y независимы, то они некоррелированы (r = 0), но из некоррелированности не следует их независимость, т.е. равенство r = 0 указывает на отсутствие линейной связи между величинами, но не на отсутствие связи между ними вообще. Пример. Закон распределения двумерной случайной величины задан таблицей
Найти ковариацию и корреляцию случайных величин Х, У. ▼ μx = M(X) = 1∙(0,10 + 0,20) + 2∙(0,15 + 0,22) + 3∙(0,12 + 0,21) =2,03; M(X2) = 1 2 ∙(0,10 + 0,20) + 2 2 ∙(0,15 + 0,22) + 3 2 ∙(0,12 + 0,21) =4,75;
μy = M(Y) = 1∙(0,10 + 0,15 + 0,12) + 2∙(0,20 + 0,22 + 0,21) = 1,63; M(Y2) = 1 2 ∙(0,10 + 0,15 + 0,12) + 2 2 ∙(0,20 + 0,22 + 0,21) = 2,89;
M(XY) = 1∙1∙0,10 + 1∙2∙0,20 + 2∙1∙0,15 + 2∙2∙0,22 + 3∙1∙0,12 + + 3∙2∙0,21 = 3,3; с ov(X,Y) = M(XY) – μxμy = 3,3 – 2,03∙1,63 =- 0,0089;
Некоторые свойства М(ХУ), D(X + Y). 1. M(XY) = M(X)M(Y) + cov(X,Y) 2. D(X + Y) = D(X) + D(Y) + 2cov(X,Y) ▼ 1. Вытекает из определения ковариации. ▼ 2.
Следствие. Для независимых случайных величин имеем: М(ХУ) = М(Х)М(У), D(X+ Y) = D(X) + D(Y).
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.48.62 (0.013 с.) |
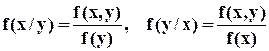 .
.
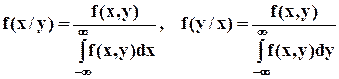 .
. .
.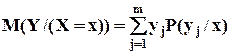 .
. ,
, ,
, 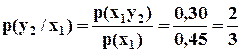 ,
,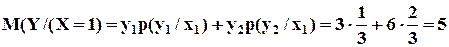 .
.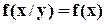 при любых наблюдаемых у;
при любых наблюдаемых у;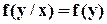 при любых наблюдаемых х.
при любых наблюдаемых х.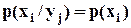 при любых наблюдаемых j;
при любых наблюдаемых j; при любых наблюдаемых i.
при любых наблюдаемых i. при всех i, j.
при всех i, j.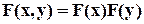 .
.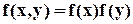 .
.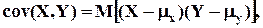 где
где 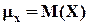 ,
, 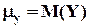 .
.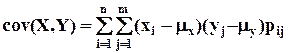 ,
,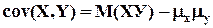 , где
, где 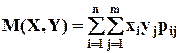 .
.
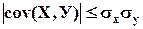 .
.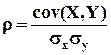 .
. 0.
0.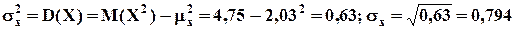 ;
; ;
;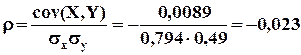 /
/