
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы математической статистики.
Вариационные ряды и их характеристик. Пусть требуется изучить совокупность однородных объектов относительно некоторого признака. Признак – характеристика объекта, рассматриваемая как случайная величина. Совокупность – множество объектов, объединенных по определенному признаку. Признак любой совокупности при наблюдении принимает ряд значений, число которых конечно. Обозначим признак совокупности через Х (случайная величина), а его значения при наблюдении через х1, х2,…, хn (числа). Числа х1, х2,…, хn образуют несгруппированные данные. Объемом совокупности (n) называется число объектов совокупности. Пример 1. В магазине за день было продано 20 пар мужской обуви. Случайная величина Х (размер обуви) приняла следующие значения 36 38 37 41 37 41 38 42 39 40 38 42 39 42 39 40 40 39 40 39 Исходные данные из n = 20 наблюдений представляют собой несгруппированные данные. Произведем группировку исходных данных. Группировка состоит в объединении данных с одинаковыми или близкими значениями признака в группы и подсчете частоты каждой группы. Для осуществления группировки ранжируем исходные данные, т.е. расположим их в возрастающем порядке. В результате получим следующий ранжированный ряд: 36 37 37 38 38 38 39 39 39 39 39 40 40 40 40 41 41 42 42 42. Некоторые данные принимают одни и те же значения, причем одни значения встречаются чаще, другие реже. Вариантами xi называются различные значения признака, встречающие в совокупности. Частотой варианты xi называется число mi, показывающее, сколько раз эта варианта встречается в совокупности., причем Σ mi = n. Частостью (относительной частотой, долей) варианты называется отношение частоты варианты к объему совокупности, т.е.
В рассматриваемом примере: - варианты xi: 36 37 38 39 40 41 42; - частоты mi: 1 2 3 5 4 2 3; - частости w i: 0,05 0,10 0,15 0,25 0,20 0,10 0,15. Вариационным рядом называется ранжированный в порядке возрастания ряд вариантов с соответствующими им весами (частотами или частостями). Вариационный ряд называется дискретным, если его варианты принимают конкретные изолированные значения, и – интервальным, если его варианты принимают любые значения из некоторого числового промежутка. Общий вид дискретного вариационного ряда
Таким образом, дискретный вариационный ряд состоит из двух элементов: варианты и частоты (частости). При изучении вариационных рядов используются также понятие накопленной частоты. Накопленная частота Накопленные частоты (частости) для каждого интервала находятся последовательным суммированием частот (частостей) всех предшествующих интервалов, включая данный, т.е
Представим сгруппированные данные рассматриваемого примера в виде таблицы
Эмпирической функцией распределения Fn(x) называется частость того, что признак (случайная величина Х) примет значение, меньше заданного х, т.е. Fn(x) = w(X < x) = Для дискретного вариационного ряда эмпирическая функция распределения представляет собой разрывную ступенчатую функцию. Для рассматриваемого примера
Для графического изображения дискретного вариационного ряда используется полигон частот (частостей) и кумулятивная кривая. Полигоном частот ( частостей) называют ломанную, отрезки которой соединяют точки (xi, mi), или (xi, wi), i = 1,2,… Кумулятивная кривая (кумулята) – кривая накопленных частот (частостей). Для дискретного ряда кумулята представляет ломанную, соединяющую точки (xi, На рис. представлены графики полигона частот и кумуляты для рассматриваемого примера.
Интервальный ряд. При построении интервального ряда произведем следующую группировку данных. Весь диапазон изменения признака в совокупности разбивают на равные интервалы шириной Δх, равной
где xmin, xmax – наименьшее и наибольшее значение признака в совокупности, а к – число интервалов. Число интервалов следует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень малым, чтобы не потерять особенности распределения признака. Рекомендуемое число интервалов определяется по формуле: k = 1 + 3,322lgn. Если окажется, что Δх - дробное число, то за длину интервала берут либо ближайшее целое число, либо ближайшую простую дробь.
За начало первого интервала рекомендуется брать величину xнач = xmin – Δх/2. Конец последнего интервала должен удовлетворять условию xкон – Δх ≤ xmax < xкон. Промежуточные интервалы получают, прибавляя к концу предыдущего интервала величину Δх. Объединяют данные, попавшие в соответствующие интервалы группировки. Если значение признака находится на границе интервала, то его присоединяют к правому интервалу. Частотой интервала называется число данных, попавших в соответствующий интервал. Частота интервала относится ко всему интервалу группировки. Иногда интервальный вариационный ряд условно заменяют дискретным, В этом случае серединное значение i – го интервала принимают за вариант xi, а соответствующую интервальную частоту mi – за частоту этого варианта.. Пример 2. Массив данных представлен следующим ранжированным рядом 10 12 14 16 17 18 19 21 22 24 24 25 25 26 26 27 27 28 29 29 31 32 32 33 33 34 34 35 36 37 38 39 39 40 41 42 43 44 45 47 Случайная величина Х приняла n = 40 значений, причем xmin = 10, xmax = 47. Произведем группировку исходных данных.
Для графического изображения интервального вариационного ряда используются гистограмма и кумулятивная кривая. Гистограмма имеет ступенчатой фигуры из прямоугольников с основаниями, равными ширине интервала Δх и высотами, равными частоте mi соответствующего интервала. При построении кумуляты интервального ряда по оси абсцисс откладываются интервалы ряда, а по оси ординат – накопленные частости. При этом необходимо помнить, что накопленная частость интервала группировки относится к верхней границе интервала. График эмпирической функции распределения Fn(x) интервального вариационного ряда совпадает с кумулятой. На рис. представлены графики гистограммы и кумуляты
Вариационный ряд является статистическим аналогом (реализации) распределения признака (случайной величины Х). В этом смысле полигон (гистограмма) аналогичен кривой распределения f(x), а эмпирическая функция распределения – функции распределения F(x) случайной величины Х.
Числовые характеристики вариационного ряда.
Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие им частоты, деленная на cуvму частот, т.е.
где xi – варианты дискретного ряда или середины интервалов интервального ряда, mi – соответствующие им частоты, n – объем ряда. Среднее арифметическое вариационного ряда характеризует значение признака, вокруг которого концентрируются наблюдения. Дисперсией σ2 вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической, т.е.
Дисперсия вариационного ряда определяет меру рассеяния признака в совокупности относительно средней арифметической. Формулу для расчета дисперсии можно преобразовать к виду
Средним квадратическим отклонением называется корень квадратный из дисперсии, т.е.
Среднее квадратическое отклонение показывает, насколько в среднем отклоняется случайная величина в совокупности относительно средней арифметической. Пример. Вычислить ▼ Исходные данные и расчетные показатели представим в виде расчетной таблицы.
Окончательно имеем
Пример. Вычислить ▼ Исходные данные и расчетные показатели представим в виде расчетной таблицы.
Окончательно имеем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.104.120 (0.029 с.) |
 , причем Σw i = 1.
, причем Σw i = 1. показывает, сколько наблюдалось вариантов со значением признака Х < х. Отношение накопленной частоты
показывает, сколько наблюдалось вариантов со значением признака Х < х. Отношение накопленной частоты  .
. .
.
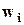
 .
.


 ,
, . Примем Δх = 6. За начало первого интервала возьмем xнач = 10 – 3 = 7, тогда получим следующие интервалы: [7; 13), [13; 19),…, [43; 49). Подсчитываем число данных, попавших в каждый интервал группировки (частоту). Результаты группировки представим в таблице
. Примем Δх = 6. За начало первого интервала возьмем xнач = 10 – 3 = 7, тогда получим следующие интервалы: [7; 13), [13; 19),…, [43; 49). Подсчитываем число данных, попавших в каждый интервал группировки (частоту). Результаты группировки представим в таблице

 ,
, .
. , где
, где  .
. .
. по данным примера 1.
по данным примера 1.


 ;
; 
 ,
,  .
.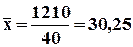 ;
; 
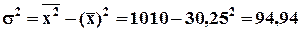 ,
,  .
.


