
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Начальные и центральные моменты.
Начальным моментом к-го порядка случайной величины Х называется математическое ожидание к-ой степени этой величины, т.е. νк = М(Хк). Для дискретной случайной величины νк = Для непрерывной случайной величины νк = Центральным моментом к-го порядка случайной величины Х называется математическое ожидание к-ой степени отклонения случайной величины от ее математического ожидания, т.е. μк = М(Х – а)к, где а = М(Х). Для дискретной случайной величины μ к = Для непрерывной случайной величины μ к = Заметим, что ν1 = М(Х) = а, μ 2 = D(Х) = σ2, Центральные моменты μ к могут быть выражены через начальные моменты νк по формулам:
Для симметричного распределения все нечетные центральные моменты равны нулю, т.е. μ1 = μ2 =…= 0, т.к. положительные и отрицательные отклонения относительно центра распределения взаимно погашаются. Моменты распределения различных порядков используются для характеристики распределения. Начальный момент 1-го порядка ν1 = М(Х) характеризует среднее значение или положение центра распределения случайной величины Х. Центральный момент 2-го порядка μ2 = D(Х) характеризует степень рассеяния Х относительно центра распределения. Центральный момент 3-го порядка μ3 характеризует отклонение распределения от симметричного Для симметричного распределения μ3 = 0.. Мерой отклонения распределения от симметричного является коэффициент асимметрии: As = μ3/σ3, -∞ < As < ∞, причем: As = 0 для симметричного распределения; As > 0 для распределения, скошенного влево; As < 0 для распределения, скошенного вправо. Центральный момент 4-го порядка μ4 характеризует отклонение симметричного распределения от нормального. Ддя нормального распределения μ4 = 3σ4. Мерой отклонения формы строения вершины симметричной кривой от нормальной является показатель эксцесса Ех = μ4 / σ4 – 3, -∞ < Ех < ∞, причем: Ех = 0 для нормального распределения; Ех > 0 для островершинного распределения; Ех < 0 для плосковершинного распределения. Пример. Определите асимметрию и эксцесс распределения случайной величины Х, заданной таблицей
▼ ν1= 1∙0,1 + 3∙0,4 + 5∙0,2 + 7∙0,2 + 9∙0,1 = 4,6; M(X) = 4,6;
ν2= 12∙0,1 + 32∙0,4 + 52∙0,2 + 72∙0,2 + 92∙0,1 = 26,6; ν3= 13∙0,1 + 33∙0,4 + 53∙0,2 + 73∙0,2 + 93∙0,1 = 177,4; ν4= 14∙0,1 + 34∙0,4 + 54∙0,2 + 74∙0,2 + 94∙0,1 = 1293,8. μ2 = ν2 -
Закон больших чисел.
Неравенство Маркова. Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, Тл для любого положительного числа А выполняется неравенство
▼ Пусть Х непрерывная случайная величина с плотностью распределения f(x). Из условия теоремы следует, что f(x)= 0 при х < 0, и f(x) ≥ 0 при х ≥ 0.
Неравенство Маркова применима к любым неотрицательным случайным величинам. Пример. Средний срок службы изделия 4 года. Оценить вероятность того, что данное изделие не прослужит более 20 лет. ▼ Случайная величина Х – срок службы изделия. По условию М(Х) = 4, А = 20, тогда Неравенство Чебышева. Для произвольно распределенной случайной величины Х с известными средним М(Х) и дисперсией D(X), вероятность ее отклонения от среднего оценивается выражением:
▼ Рассмотрим случайную величину Y = (X – M(X))2 ≥ 0. M(Y) = M(X – M(X))2 = D(X). Применим к У неравенство Маркова, получим;
Пользуясь неравенством Чебышева, можно оценить вероятность тех или иных отклонений от среднего значения независимо от природы случайной величины (грубая оценка). Пример. Оценить вероятность того, что отклонение любой случайной величины Х от ее математического ожидания по модулю будет меньше трех стандартных отклонений этой величины. ▼ Пусть Х – случайная величина, D(X) = σ2, тогда
В случае нормального распределения эта вероятность
Следствие. Если случайная величина Х = m распределена по биномиальному закону, то вероятность отклонения частоты m от среднего M(m) = np и частости m/n от среднего M(m/n) = p оценивается выражением:
Пример. В среднем 70% покупателей магазина делают покупку. Оценить с помощью неравенства Чебышева вероятность того, что из 1000 человек, посетивших магазин, число покупателей, сделавших покупку, заключено в границах от 620 до 780.
▼ Считаем, что случайная величина Х = m (число покупателей, сделавших покупку) распределено по биномиальному закону. По условию n = 1000, p = 0,7; q = 0,3; 620 < m < 780. Требуется оценить вероятность Р(620 < m < 780). Заметим, что M(m) = np = 1000∙0,7 = 700, а неравенство 620 < m < 780 можно записать как | m - 700| < 80, т.е. ε = 80. Используя неравенство Чебышева, получим
Более точный результат получим при использовании следствия из интегральной теоремы Муавра – Лапласа:
Теорема Чебышева. При достаточно большом числе nпопарно независимых случайных величин Х1, Х2,…, Хn с дисперсиями, ограниченными одной и той же постоянной, вероятность того, что сколь угодно мало отклонение среднего арифметического этих величин от среднего арифметического их математических ожиданий, стремится к единице, т.е.
▼ Пусть
Следствие. Если независимые случайные величины Х1, Х2,…, Хn имеют одинаковые математические ожидания, равные μ, и их дисперсии ограничены одной и той же постоянной, то
Согласно этой теореме среднее арифметическое достаточно большого числа случайных величин утрачивает характер случайной величины и ведет себя почти как постоянная величина. Эта теорема имеет важное значение для статистики, обосновывая выбор среднего арифметического выборочных величин в качестве оценки математического ожидания (среднего значения) всей совокупности. Пример. Сколько надо провести измерений данной величины, чтобы с вероятностью 0,95 гарантировать отклонение средней арифметической этих величин от истинного значения не более, чем на 1 (по абс. величине), если дисперсия каждого измерения не превосходит 25. ▼ Пусть Х1, Х2,…, Хn – результаты измерений. По условию М(Хi) = μ – истинное значение, D(Хi) = 25. Необходимо найти n, при котором
Из следствия теоремы Чебышева Теорема Бернулли. При достаточно большом числе n независимых испытаний вероятность того, что сколь угодно малым будет отклонение частости m/n события от вероятности р наступления этого события, при условии, что она постоянно в каждом испытании, стремится к единице, т.е.
Эта теорема имеет важное значение для статистики, обосновывая выбор частости события в качестве оценки вероятности этого события. Центральная предельная теорема. Распределение суммы n произвольно распределенных и взаимно независимых случайных величин при n → ∞ стремится к нормальному, если вклад отдельных слагаемых в сумму равномерно мал. Множество факторов, определяющих тот или иной экономический показатель достаточно велико, и при выполнении условий теоремы, отклонение этого показателя от среднего значения может быть приближенно описано нормальным распределением.
Двумерные случайные величины.
Двумерной называют случайную величину (Х,У), возможные значения которой есть пары чисел (х,у). Геометрически двумерную величину можно рассматривать как случайную точку М(Х,У) на плоскости, либо как случайный вектор ОМ. Дискретной называют двумерную величину, составляющие Х, У которой дискретны. Непрерывной называют двумерную величину, составляющие которой непрерывны.
Законом распределения вероятностей двумерной случайной величины называют соответствие между возможными значениями (Х, У) и их вероятностями.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 6233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.168.172 (0.023 с.) |
 .
. .
. .
. .
.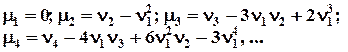
 = 26,6 – 4,62 = 5,44; D(X) = 5,44;
= 26,6 – 4,62 = 5,44; D(X) = 5,44;  ;
; = 177,4 -3∙4,6∙26,6 + 2∙4,63 = 4,992;
= 177,4 -3∙4,6∙26,6 + 2∙4,63 = 4,992; = 64,95;
= 64,95; ,
,  .
.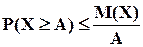 , или
, или  .
.
 . Получили
. Получили  , или
, или  .
. .
. , или
, или  .
. . Подставим в это неравенство выражение У через Х и А = ε2, получим
. Подставим в это неравенство выражение У через Х и А = ε2, получим  , или
, или , или
, или  .
. , что не противоречит полученному результату.
, что не противоречит полученному результату. ,
,  .
.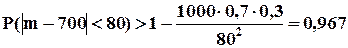 .
.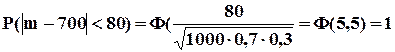 .
. .
.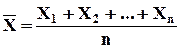 , тогда
, тогда ,
,  . Применяя к величине
. Применяя к величине  неравенство Чебышева, получим:
неравенство Чебышева, получим: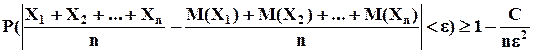 , или
, или , и
, и  .
. .
. , т.е.
, т.е.  , где ε =1, С = 25, тогда
, где ε =1, С = 25, тогда  , n ≥ 500.
, n ≥ 500. .
.


