
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гипотеза о неизвестном среднем при неизвестной дисперсии.
Если дисперсия генеральной совокупности неизвестна, то в качестве критерия проверки нулевой гипотезы принимают случайную величину
где S – исправленное стандартное отклонение в выборке. Величина t имеет распределение Стьюдента с ν = n – 1 степенями свободы. Критическая область строится в зависимости от вида конкурирующей гипотезы. Критическую точку t кр находят по таблице распределения Стьюдента из условия:
Если | tнаб | < t кр, то H0 принимается, если | tнаб | > t кр, то H0 отклоняется. Замечание. В Excel имеется функция
а) H1: ▼ Найдем наблюдаемое значение критерия
а) По условию H1: Поскольку | tнаб | = 2 < t кр= 2,13,то H0 принимается, т.е. выборочная средняя б) По условию H1: Поскольку | tнаб | = 2 > t кр= 1,75,то H0 отклоняется, т.е. различия между выборочной и предполагаемой средними - значимое. Пример. Производитель утверждает, что средний вес пачки чая не меньше 100 г. Инспектор отобрал 10 пачек чая и взвесил. Их вес оказался равным 97 102 103 98 96 105 98 100 101 98. При заданном уровне значимости 0,01 проверить утверждение производителя. ▼ Гипотезы Найдем выборочные
Найдем наблюдаемые значения критерия
По условию H1: Поскольку | tнаб | = 0,111 < t кр= 2,82,то H0 принимается, т.е. утверждение производителя справедливо.
Гипотеза о неизвестной частоты появления события. Пусть по достаточному большому числу n независимых испытаний, в каждом из которых вероятность р появления события постоянно, но неизвестна, найдена относительная частота w = m/n.
Пусть имеется основание предполагать, что неизвестная вероятность равна р0. Требуется при заданном уровне значимости α проверить нулевую гипотезу, что неизвестная вероятность р равна предполагаемой вероятности р0, т.е. Н0: р = р0. В качестве критерия проверки нулевой гипотезы принимается случайная величина
Величина z при справедливости нулевой гипотезы приближенно нормально. Критическая область строится в зависимости от вида конкурирующей гипотезы. Пример. Партия изделий принимается, если доля брака составляет менее 2%. Среди случайно отобранных 500 изделий оказалось 13 бракованных. Следует ли на уровне значимости 0,05 принять партию. ▼ По условию n = 500, m = 13, р0 = 0,02, α = 0,05. Гипотезы Относительная частота (частость) составляет Найдем наблюдаемое значение критерия
По условию H1: р < 0,02, поэтому критическая область – односторонняя. По таблице функции Лапласа найдем критическую точку zкр = zкр (1 - 2α) = zкр (0,9) = 1,65. Поскольку | zнаб | = 0,96 < zкр= 1,65,то H0 принимается, т.е. партия изделий принимается. Пример. Торговец утверждает, что он получает заказы в среднем от 30% предполагаемых клиентов. Можно ли при 5% - ом уровне значимости считать, что утверждение верно, если он получил заказы от 20 из 100 клиентов. ▼ По условию n = 100, m = 20, р0 = 0,3, α = 0,05. Гипотезы Относительная частота (частость) составляет Найдем наблюдаемое значение критерия
По условию H1: р ≠ 0,3, поэтому критическая область – двусторонняя. По таблице функции Лапласа найдем критическую точку zкр = zкр (1 - α) = zкр (0,95) = 1,96. Поскольку | zнаб | = 2,18 > zкр= 1,96,то H0 отклоняется, т.е. утверждение торговца неверно.
Гипотеза о значимости выборочного коэффициента корреляции. Пусть по данным выборки объема n получен выборочный коэффициент корреляции r ≠ 0. Требуется проверить гипотезу о равенстве нулю истинного значения коэффициента корреляции ρ. Выдвигаются гипотезы В качестве критерия проверки нулевой гипотезы принимается случайная величина
которая имеет распределение Стьюдента с ν = n – 2 степенями свободы. Поскольку Н1: ρ ≠ 0, то критическая область – двусторонняя.
Критические точки определяются по таблице распределения Стьюдента из условия: t кр= t кр(1 – α; ν). Если | tнаб | < t кр, то H0 принимается, т.е. r незначим, если | tнаб | > t кр, то H0 отклоняется, т.е. r значим. Пример. Пусть по выборке объема n = 122, извлеченной из нормальной совокупности, получен выборочный коэффициент корреляции r = 0,4. При уровне значимости 0,05 установить значимость выборочного коэффициента корреляции. ▼ Найдем наблюдаемое значение критерия
Критическую точку определяются по таблице распределения Стьюдента из условия: t кр= t кр(1 – α; ν) = t кр( 0,95;120 ) = 1,98. Поскольку| tнаб | = 4,78 > t кр= 1,98, то H0 отклоняется, т.е. выборочный коэффициент корреляции r = 0,4значимо отличается от нуля.
Гипотеза о неизвестной генеральной дисперсии.
Пусть из генеральной совокупности, распределенной нормально, извлечена выборка объема n и по ней найдена исправленная выборочная дисперсия S2. Требуется по исправленной дисперсии при заданном уровне значимости проверить нулевую гипотезу, что неизвестная генеральная дисперсия равна предполагаемому значению В качестве критерия проверки нулевой гипотезы принимают случайную величину (хи – квадрат):
которая имеет распределение хи – квадрат с ν = n – 1 степенями свободы. Распределение хи – квадрат не симметричное. Критическая область строится в зависимости от вида конкурирующей гипотезы. В случае Н1: М (S2) < По таблице критических точек распределения хи – квадрат находят левую критическую точку Если В случае Н1: М (S2) > По таблице критических точек распределения хи – квадрат находят правую критическую точку Если В случае Н1: М (S2) ≠ По таблице критических точек распределения хи – квадрат находят левую критическую точку Если Замечание. В Excel имеется функция
а для двусторонней критической области:
Пример. Из нормальной генеральной совокупности извлекается выборка объема n = 13 и по ней найдена исправленная выборочная дисперсия S2 =10,3. Требуется при уровне значимости 0,02 проверить гипотезу Н0: М (S2) = 12 при конкурирующей гипотезе: а) Н1: М (S2) ≠ 12; б) Н1: М (S2) > 12. ▼ Найдем наблюдаемое значение критерия
а) Поскольку Н1: М (S2) ≠ 12, то критическая область двусторонняя. По таблице критических точек распределения хи – квадрат найдем Поскольку б) Поскольку Н1: М (S2) > 12, то имеем правостороннюю критическую область. По таблице критических точек распределения хи – квадрат найдем правую критическую точку Поскольку
Критерий согласия Пирсона. Критерий согласия – это критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Пусть требуется проверить гипотезу, что случайная величина Х распределена по нормальному закону, т.е. Х ~ N( На основании выборки x1, x2,…,xn объема n эту гипотезу надо принять или опровергнуть при заданном уровне значимости. Разобьем весь интервал наблюдаемых значений Х на к – равных интервалов, а в качестве эмпирической частоты mi принимаем число значений случайной величины Х, попавших в i –ый интервал. В результате получим следующий ряд распределения
Вычисляем выборочные среднюю Неизвестные параметры (
Поскольку объем выборочной совокупности равен n, то теоретическая частота соответствующего интервала определяется как В качестве критерия проверки нулевой гипотезы принимается случайная величина
где Наблюдаемое значение критерия Если Пример. По данным распределения объема товарооборота магазинов района проверить гипотезу о нормальности распределения. ▼ Случайная величина Х – объемы товарооборота магазинов. Исходные данные и расчетные показатели представим в расчетной таблице.
Окончательно имеем
Полагаем
причем полагают α1 = - ∞, βк = ∞. Результаты расчета представим в таблице
Сравним эмпирические и теоретические частоты
Получили По таблице Поскольку
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.18.48 (0.063 с.) |
 ,
,
 Пример. По выборке объема n = 16 найдены выборочная средняя
Пример. По выборке объема n = 16 найдены выборочная средняя 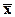 = 18,2 и исправленное стандартное отклонение S = 3,6. Требуется по уровню значимости 0,05 проверить нулевую гипотезу H0:
= 18,2 и исправленное стандартное отклонение S = 3,6. Требуется по уровню значимости 0,05 проверить нулевую гипотезу H0:  = 120 при конкурирующей гипотезе:
= 120 при конкурирующей гипотезе: .
.
 ;
;  ;
;  .
.
 , где
, где  .
. .
. .
. .
. .
. .
. .
. .
. ,
, .
. , т.е Н0: М (S2) =
, т.е Н0: М (S2) =  ,
, .
. <
<  , то H0 отвергается, если
, то H0 отвергается, если  .
. и правую
и правую  .
. <
<  , то H0 принимается, иначе отвергается.
, то H0 принимается, иначе отвергается. .
. ,
,  .
. .
. ).
).





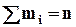



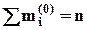
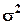 .
. .
. .
. ,
, - эмпирические и теоретические частоты в i –ом интервале; к – число интервалов. Этот критерий согласия был предложен Пирсоном.
- эмпирические и теоретические частоты в i –ом интервале; к – число интервалов. Этот критерий согласия был предложен Пирсоном. , определяемое по таблице при заданном уровне значимости α и числу степеней свободы ν = k – r – 1, где r – число параметров распределения, к – число интервалов.
, определяемое по таблице при заданном уровне значимости α и числу степеней свободы ν = k – r – 1, где r – число параметров распределения, к – число интервалов.



 ;
; 
 ,
,  .
.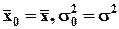 . Теоретические частоты
. Теоретические частоты  в i –ом интервале определяются из выражения:
в i –ом интервале определяются из выражения: 




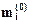

 .
.


