Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимизация конъюнктивных нормальных формСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для построения минимальной конъюнктивной нормальной формы (МКНФ) функции f нужно построить минимальную ДНФ функции Пример. Построить минимальную КНФ функции f из примера (*). Решение: Построим таблицу истинности для функции
Строим СДНФ функции СДНФ Строим СКНФ функции СКНФ Раскроем скобки в выражении для СКНФ функции
Составим таблицу покрытий.
Решеточное выражение равно 34(2 = 34(1 Выражению 134 соответствует тупиковая ДНФ функции Выражению 234 соответствует тупиковая ДНФ функции Так как обе тупиковые ДНФ функции В формуле Минимизация в классе нормальных форм Для того, чтобы построить минимальную нормальную форму (МНФ) функции f, необходимо выполнить следующие действия: 1. Построить все минимальные ДНФ функции f. 2. Найти все минимальные КНФ функции f. 3. Из полученных форм нужно выбрать форму с наименьшим числом переменных и отрицаний переменных. Это и есть минимальная нормальная форма (МНФ) функции f. Пример. Построить минимальную нормальную форму (МНФ) функции f из примера (*) Решение: Минимальная ДНФ функции f равна
Задачи для самостоятельного решения 1. Построить СДНФ, СКНФ, сокращённую ДНФ, тупиковую и минимальную ДНФ, минимальную КНФ, минимальную нормальную форму для функции f, таблица истинности которой имеет следующий вид:
а).
б).
в).
г).
д).
Практическое занятие №4 Основные понятия теории графов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 1068; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.67.228 (0.01 с.) |

 и в полученной минимальной ДНФ заменить знак & на знак
и в полученной минимальной ДНФ заменить знак & на знак  , знак
, знак  (
( - двойное отрицание).
- двойное отрицание).
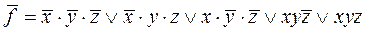 .
. .
.



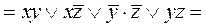 сокр. ДНФ
сокр. ДНФ 

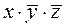






 3)(1
3)(1  , которая содержит 6 переменных и отрицаний переменных.
, которая содержит 6 переменных и отрицаний переменных.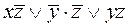 , которая содержит 6 переменных и отрицаний переменных.
, которая содержит 6 переменных и отрицаний переменных. . Это и будет минимальная КНФ функции f.
. Это и будет минимальная КНФ функции f. . Это минимальная КНФ функции f.
. Это минимальная КНФ функции f. и содержит 5 переменных и отрицаний переменных. Обе минимальные КНФ функции f (
и содержит 5 переменных и отрицаний переменных. Обе минимальные КНФ функции f (