
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волгоградский кооперативный институт (филиал)Стр 1 из 5Следующая ⇒
Волгоградский кооперативный институт (филиал) Кафедра естественнонаучных и математических дисциплин И.А. Генералова
ДИСКРЕТНАЯ МАТЕМАТИКА
Учебно-методический комплекс для студентов направления 230700.62 «Прикладная информатика» заочной формы обучения
Волгоград 2012
Рецензент: Акопян Р.С. к.ф.м.н., доцент кафедры естественнонаучных и математических дисциплин Волгоградского кооперативного института (филиала) Российского университета кооперации
Генералова И.А. Учебно-методический комплекс для студентов направления 230700.62 «Прикладная информатика» заочной формы обучения. - Волгоградский кооперативный институт. Волгоград 2012. - 56 с.
Данное издание ориентировано на студентов направления 230700.62 «Прикладная информатика» заочной формы обучения, составлено на основании лекционного курса, содержит краткую теорию, примеры решения задач по разделам курса «Дискретная математика», задачи для самостоятельного решения.
Рассмотрено и одобрено на заседании кафедры естественнонаучных и математических дисциплин, протокол № 1 от 29.08. 2011 г.
© АНО ВПО ЦС РФ Волгоградский кооперативный институт (филиал) Российского университета кооперации, 2012 © Генералова И.А., 2012
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Дискретная математика – область математики, занимающаяся изучением свойств дискретных структур, которые возникают как внутри математики, так и в ее приложениях. К числу таких структур могут быть отнесены, например, конечные группы, конечные графы, а также некоторые математические модели преобразователей информации. Для многих задач дискретной математики средства классической математики оказываются мало приемлемыми. Это объясняется необходимостью отказа в дискретной математике от основополагающих понятий классической математики – предела и непрерывности. Вместе с задачами о существовании, имеющими общематематический характер, важное место в дискретной математике занимают задачи, связанные с алгоритмической разрешимостью и построением конкретных алгоритмов. Цели и задачи освоения учебной дисциплины Преподавание дисциплины «Дискретная математика» при подготовке специалиста имеет цель: - изучение свойств объектов конечного характера, различных аспектов построения математических моделей, возникающих при исследовании информационных процессов и процессов управления в различных областях практической деятельности; - развить логическое мышление, общий уровень математической культуры; - сформировать компетенции обучающегося в области применения математических методов и средств при решении прикладных задач, связанных с алгоритмической разрешимостью и построением конкретных алгоритмов. В результате изучения дисциплины студент должен: знать: - основные определения и теоремы из комбинаторики, теории графов и алгебры логики; иметь представление о методах дискретной математики; знать о новейших достижениях в дискретной математике; уметь: - строить математические модели дискретных структур; - выбирать подходящий математический метод и алгоритм для решения сложных задач исследования информационных процессов и процессов управления;
- выработать, на основе проведенного математического анализа, практические рекомендации для решения прикладных задач; владеть: - навыками моделирования прикладных задач методами дискретной математики. Методические указания студентам: - при подготовке к практическим занятиям студентам следует использовать литературу из приведённого списка, а также руководствоваться указаниями и рекомендациями преподавателя; - перед каждым практическим занятием студент изучает план занятия с перечнем тем и вопросов по вынесенному на семинар материалу. Студенту рекомендуется следующая схема подготовки к практическому занятию: - проработать конспект лекций; - изучить решения типовых задач; - решить заданные домашние задания; - при затруднениях сформулировать вопросы к преподавателю. Домашние задания необходимо выполнять к каждому практическому занятию. Сложные вопросы можно вынести на обсуждение на семинар или на индивидуальные консультации. На практических занятиях приветствуется способность на основе полученных знаний находить наиболее эффективное решение поставленных проблем. ТЕМАТИЧЕСКИЙ ПЛАН
нормативная заочная форма обучения
сокращенная заочная форма обучения (на базе СПО)
ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ, МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИЗУЧЕНИЮ ТЕМ И ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ Практическое занятие №1 Размещения Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число размещений из n элементов по m элементов обозначают
Понятие факториала Произведение n натуральных чисел от 1 до n обозначается символом n! (n факториал), то есть Например, 2!= 3!= 5!= Заметим, что удобно рассчитывать 0!, полагая по определению, 0!=1. Примеры:
Из последних двух формул следует, что
Пример. В однокруговом турнире по футболу участвуют 8 команд. Сколько существует вариантов призовой тройки? Решение: Так как порядок команд в призовой тройке важен, то мы имеем дело с размещениями. Тогда
Пример. Сколькими способами можно выбрать три лица на три различные должности из десяти кандидатов? Решение:
Пример. Сколько можно составить телефонных номеров из 5 цифр так, чтобы в каждом отдельно взятом номере все цифры были различными? Решение:
Перестановки Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок из n элементов обозначают Pn (P – первая буква французского слова permutation, что означает перестановка) и вычисляют по формуле:
Пример. В финальном забеге на 100 метров участвуют 8 спортсменов. Сколько существует вариантов протокола забега? Решение: В данном случае речь идёт обо всех перестановках из 8 элементов. Тогда
Пример. Сколькими различными способами могут разместиться на скамейке10 человек? Решение:
Пример. Сколькими способами можно разместить 7 лиц за столом, на котором поставлено 7 столовых приборов? Решение:
Сочетания Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний вычисляют по формуле: Пример. Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов? Решение:
Пример. Сколькими способами можно выбрать три детали из ящика, содержащего 15 деталей? Решение:
Другой вид формул числа размещений и числа сочетаний
Свойства числа сочетаний: 1) 2) 3) 4) 5) При решении задач комбинаторики используют следующие правила: Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В – k способами, то объект «либо А, либо В» можно выбрать n+k способами.
Правило произведения. Если некоторый объект А может быть выбран из совокупности объектов n способами и после каждого такого выбора другой объект В – k способами, то пара объектов (А, В) в указанном порядке может быть выбрана n×k способами.
Если некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Размещения с повторениями Число размещений по m элементов с повторениями из n различных элементов равно nm,то есть Пример. Из цифр 1,2,3,4,5 можно составить 53 =125 трехзначных чисел, если в одном и том же числе могут попадаться и одинаковые цифры. Перестановки с повторениями Если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., то число перестановок с повторениями
Пример. Сколько различных перестановок букв можно сделать в слове «математика»? Решение:
Сочетания с повторениями Число сочетаний с повторениями из n различных элементов по m элементов равно числу сочетаний без повторений из (n + m -1) различных элементов по m элементов:
Пример. Найти число сочетаний с повторениями из четырех элементов a, b, c, d по 3 элемента. Решение: Искомое число будет Бином Ньютона Для произвольного положительного целого числа n справедлива следующая формула:
Это бином Ньютона. Коэффициенты При n = 2 получим формулу При n = 3 получим формулу Пример. Определить разложение Решение:
Биномиальные коэффициенты обладают рядом свойств: 1. 2. 3. 4. Рассмотрим следующий треугольник:
…………………………. Строка под номером n содержит биномиальные коэффициенты разложения 1 1 1 2 1 1 3 3 1 1 4 6 4 1 ………………………. Это треугольник Паскаля. Он позволяет быстро найти значения биномиальных коэффициентов. Решение примеров рекомендуется выполнять в среде табличного процессора MS Excel. При этом надо учитывать некоторую терминологическую путаницу. В русскоязычной литературе перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются либо составом элементов, либо их порядком, обычно называют размещениями, а под перестановками понимают всю совокупность комбинаций, состоящих из одних и тех же n различных элементов и отличающихся только порядком их расположения. В этом смысле число всех возможных перестановок для множества из n различных элементов считается по формуле факториала Pn = n! или в Excel «=ФАКТР(N)» (см. рис. № 1)
Рис. 1
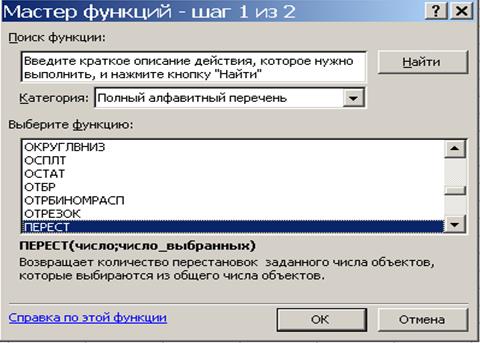
В Excel считать «перестановки», т.е. размещения, очень удобно, не нужно даже вычислять факториалы (см. рис. №2 и №3): «=ПЕРЕСТ(N;K)». Вместо N и K задаются целые положительные числа, N≥K.
Рис. 2
Рис. 3
Например, если ввести «=ПЕРЕСТ(3;2)», получим 6. Это 6 комбинации: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2). А вот встроенная функция «=ЧИСЛКОМБ(N;K)» выдает комбинаторную формулу, называемую у нас «Число сочетаний». В русскоязычной литературе так именуют перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются только составом элементов, а порядок их выбора безразличен (см. рис, №4)
Рис. 4
При использовании встроенных функций пользуйтесь «Справкой по этой функции». Например:
Задачи для самостоятельного решения 1. Вычислить: 2. Вычислить: 3. Вычислить: 4. Найти n, если 5Сn3 = 5. Найти n, если
6. Найти n, если
7. Найти n, если
8. Найти n, если
9. Решить уравнение
10. Решить систему 11. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
12. Сколькими способами можно выбрать четыре лица на четыре различные должности из девяти кандидатов?
13. Сколько можно составить телефонных номеров из 6 цифр так, чтобы в каждом отдельно взятом номере все цифры были различны?
14. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в один день?
15. Сколько можно записать четырёхзначных чисел, используя без повторения все 10 цифр?
16. Фирма производит выбор из девяти кандидатов на три различные должности. Сколько существует способов такого выбора?
17. В восьмом классе изучается 15 предметов. Сколькими способами можно составить расписание на среду, если известно, что в этот день должно быть 6 уроков?
18. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?
19. Сколькими способами можно разместить 9 лиц за столом, на котором поставлено 9 приборов?
20. На собрании выступят 6 ораторов. Сколькими способами их фамилии можно расположить в списке?
21. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
22. Сколькими различными способами можно расставить 10 различных книг на полке, чтобы определённые 4 книги стояли рядом?
23. В однокруговом турнире по футболу участвуют 8 команд. Сколько всего матчей будет сыграно?
24. Из 25 студентов нужно выбрать трех делегатов на конференцию. Сколькими способами это можно сделать?
25. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
26. В колоде 36 карт, из них 4 туза. Сколькими способами можно извлечь 6 карт так, чтобы среди них было 2 туза?
27. Комплексная бригада состоит из двух маляров, трёх штукатуров и одного столяра. Сколько различных бригад можно создать из рабочего коллектива, в котором 15 маляров, 10 штукатуров и 5 столяров?
28. В отборочном турнире за 3 путёвки на чемпионат мира участвуют 10 команд. Сколько существует вариантов «счастливой тройки»?
29. Из 12 человек выбирают четверых для назначения на 4 одинаковые должности. Сколькими способами можно сделать такой выбор?
30. Сколькими различными способами можно составить разведывательную группу из 3-х солдат и одного командира, если имеется 12 солдат и 3 командира?
31. На плоскости дано n точек, из которых никакие три не лежат на одной прямой. Найти число прямых, которые можно получить, соединяя точки попарно.
32. Буквы азбуки Морзе образуются как последовательность точек и тире. Сколько различных букв можно образовать, если использовать 5 символов?
33. Сколько существует различных семизначных телефонных номеров?
34. Пусть буквы некоторой азбуки образуются как последовательность точек, тире и пробелов. Сколько различных букв можно образовать, если использовать 5 символов?
35. При игре в бридж между четырьмя игроками распределяется колода карт в 52 листа по 13 карт каждому игроку. Сколько существует различных способов раздать карты?
36. В почтовом отделении продаются открытки пяти видов. Определить число способов покупки семи открыток.
37. Два коллекционера обмениваются марками. Найти число способов обмена, если первый коллекционер обменивает 3 марки, а второй – 6 марок. (Обмен происходит по одной марке).
38. У одного студента 6 книг по математике, а у другого – 5. Сколькими способами они могут обменять 2 книги одного на 2 книги другого?
39. Сколько различных перестановок букв можно сделать в словах: «замок», «ротор», «обороноспособность», «колокол», «семинар»?
40. Сколькими различными способами можно разместить в 9 клетках следующие 9 букв: а, а, а, б, б, б, в, в, в?
41. В автомашине 6 мест. Сколькими способами 6 человек могут сесть в эту машину, если занять место водителя могут только двое из них?
42. Сколькими способами из колоды в 52 карты можно извлечь 6 карт, содержащих туза и короля одной масти?
43. Определить разложение 44. Определить разложение 45. Найти член разложения 46. Найти шестой член разложения
47. В разложении
48. В разложении бинома 49. Найти номер того члена разложения
Практическое занятие №2 (интерактивное занятие в малых группах) Булевы функции Цель занятия: уметь строить различные булевы функции, проверять эквивалентность булевых формул (используя таблицу истинности), определять существенные и фиктивные переменные. План занятия: 1. Основные операции 2. Булевы функции от n переменных 3. Основные эквивалентности 4. Формулы
Основные эквивалентности. 1. Коммутативность:
2. Ассоциативность:
3. Дистрибутивность:
4. Правила де Моргана:
5. Законы поглощения:
6.
Приоритет конъюнкции выше, чем приоритеты дизъюнкции и суммы по модулю 2. Благодаря этому, часто удаётся опустить ряд ненужных скобок. Переменная Пример. Определить существенные и фиктивные переменные функции (11110011). Решение: Для удобства приведем таблицу истинности.
Проверим, является ли переменная x существенной или фиктивной. Рассмотрим значения функции на наборах, соседних по переменной x: f (0,0,0) = 1, f (1,0,0) = 0. f (0,0,0) ≠ f (1,0,0). Значит, переменная x – существенная. Рассмотрим теперь значения функции на наборах, соседних по переменной y: f (0,0,0) = 1, f (0,1,0) = 1. f (0,0,1) = 1, f (0,1,1) = 1. f (1,0,0) = 0, f (1,1,0) = 1. f (1,0,0) ≠ f (1,1,0). Следовательно, переменная y – существенная. Рассмотрим значения функции на наборах, соседних по переменной z: f (0,0,0) = 1, f (0,0,1) = 1. f (0,1,0) = 1, f (0,1,1) = 1. f (1,0,0) = 0, f (1,0,1) = 0. f (1,1,0) = 1, f (1,1,1) = 1. На всех парах соседних по переменной z наборов значений переменных функция принимает равные значения, следовательно, переменная z – фиктивная. Две функции алгебры логики называются равными, если одну из них можно получить из другой путём добавления и изъятия любого числа фиктивных переменных. Пусть имеется некоторое множество булевых функций F = { f 1 (…), f 2 (…), …, fn (…), …}. Введем понятие формулы над F: 1) Любая функция из F называется формулой над F. 2) Если 3) Только те объекты называются формулами над F, которые можно построить с помощью пунктов 1 и 2 данного определения. Замечание. Среди Пример. Множество Каждая формула над F реализует некоторую булеву функцию. Поэтому будем отождествлять формулу с реализуемой функцией. Задачи для самостоятельного решения 1. Определить таблицу истинности булевой функции: а) б) в) г) д) е) ж) з) и) к)
2. Используя таблицы истинности, проверить эквивалентность булевых формул. Определить существенные и фиктивные переменные. а) б) в) г) д) е) ж) з) и) 3. Решить систему уравнений
а)
б)
в) Практическое занятие №3 Нормальные формы. Минимизация нормальных форм [6]. Цель занятия: уметь строить СДНФ и СКНФ, сокращённую ДНФ, тупиковую и минимальную ДНФ, минимальную КНФ по таблице истинности. План занятия: 1. Совершенная дизъюнктивная нормальная форма (СДНФ). 2. Совершенная конъюнктивная нормальная форма (СКНФ). 3. Минимизация дизъюнктивных и конъюнктивных нормальных форм. Сокращённая ДНФ Сокращённая ДНФ функции f есть дизъюнкция всех простых импликантов функции f. Всякая функция реализуется своей сокращённой ДНФ. Для любой функции, не равной тождественно нулю, существует единственная сокращённая ДНФ. Практическое занятие №4 Основные понятия теории графов. Эйлеров цикл Теория графов берёт своё начало с решения в 1736 году знаменитым математиком Эйлером задачи о кенигсберских мостах. Жителей Кенигсберга заинтересовал вопрос, могут ли они, начав путь с одного участка суши, обойти все семь мостов, посетив каждый из мостов однажды, и вернуться в пункт старта, не переплывая реки. Эйлер переформулировал задачу, изобразив участки суши в виде вершин, а мосты – в виде рёбер графа. Тогда задача сводится к задаче о существовании в графе цикла, включающего все вершины графа. Такой цикл называется эйлеровым. Связный граф называется эйлеровым, если он содержит эйлеров цикл. Теорема. В графе с более чем одной вершиной есть эйлеров цикл тогда и только тогда, когда граф является связным и каждая его вершина имеет чётную степень. Граф, в котором существует эйлеров цикл, можно нарисовать, не отрывая карандаш от листа бумаги и не проводя дважды по какому-либо ребру графа. Пример. Определить наличие эйлерова цикла в следующем графе:
Решение: Так как в данном графе есть вершины нечётной степени, то в этом графе эйлерова цикла не существует. С помощью графов можно производить расчёт различных структур. Если структура достаточно сложная, то для решения задачи необходимо использовать компьютер. При автоматизированных работах граф неудобно задавать графически. Проще представлять его в виде двумерного массива или матрицы. Матрицей смежности графа, содержащего n вершин, называется матрица Для орграфа:
Пример. Для графа G построить матрицу смежности A(G) G
Решение: Так как у графа G 6 вершин, то размер матрицы смежности A(G) будет A(G) =
Можно заметить, что матрица смежности является симметричной, и количество единиц в каждой строке равно степени вершины, которой соответствует эта строка. По матрице смежности легко построить графическое представление графа.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.4.181 (0.281 с.) |
 (А – первая буква французского слова arrangement, что означает размещение, приведение в порядок) и вычисляют по формуле:
(А – первая буква французского слова arrangement, что означает размещение, приведение в порядок) и вычисляют по формуле:


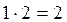





 (вариантов).
(вариантов). (способов).
(способов). (телефонных номеров).
(телефонных номеров).
 (вариантов)
(вариантов) (способов)
(способов) (способов).
(способов). (С - первая буква французского слова combinasion).
(С - первая буква французского слова combinasion). (способов).
(способов). (способов).
(способов). ;
;  , то есть
, то есть  .
.





 где
где 


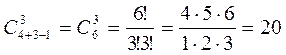
 .
. называются биномиальными коэффициентами.
называются биномиальными коэффициентами. ;
; .
. при n=4.
при n=4.
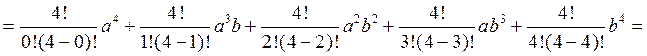
 .
. ;
; ;
; ;
; .
.



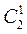
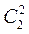
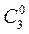

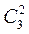

 . Воспользовавшись свойством
. Воспользовавшись свойством 








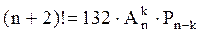

 , k
, k 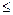 n
n

 при n=5.
при n=5.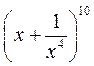 , не содержащий x (то есть содержащий x в нулевой степени).
, не содержащий x (то есть содержащий x в нулевой степени). , если биномиальный коэффициент третьего от конца члена равен 45.
, если биномиальный коэффициент третьего от конца члена равен 45.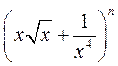 коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, то есть член разложения, не зависящий от x (членом, не зависящим от x, будет тот, который содержит x в нулевой степени).
коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, то есть член разложения, не зависящий от x (членом, не зависящим от x, будет тот, который содержит x в нулевой степени). найти члены, не содержащие иррациональности.
найти члены, не содержащие иррациональности. , который содержит a и b в одинаковых степенях.
, который содержит a и b в одинаковых степенях. ;
; ;
; ;
;
 ;
;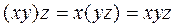 ;
;
 ;
; ;
;
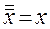
 ,
, .
.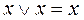 ;
; ;
; ;
; ;
; ;
;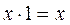 ;
; ;
;





 называется существенной переменной функции
называется существенной переменной функции  , если существуют такой набор
, если существуют такой набор  переменных, что значение функции
переменных, что значение функции  .Такие наборы, отличающиеся лишь одной переменной
.Такие наборы, отличающиеся лишь одной переменной  , называются соседними по
, называются соседними по  F и
F и 
 — либо переменная, либо формула над F, то выражение вида
— либо переменная, либо формула над F, то выражение вида  является также формулой над F.
является также формулой над F. вполне могут быть одинаковые.
вполне могут быть одинаковые.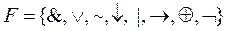 . Тогда
. Тогда  ,
,  ,
,  - формулы над F. Иногда внешние скобки у формул опускают.
- формулы над F. Иногда внешние скобки у формул опускают. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;



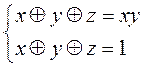

 с n строками и n столбцами, каждый элемент которой
с n строками и n столбцами, каждый элемент которой  определяется по следующей формуле:
определяется по следующей формуле: 


 . Используя определение для матрицы смежности, получим:
. Используя определение для матрицы смежности, получим:
 , так как в графе существует ребро, соединяющее вершины
, так как в графе существует ребро, соединяющее вершины  и
и  .
. , так как в графе существует ребро, соединяющее вершины
, так как в графе существует ребро, соединяющее вершины  .
. , так как в графе нет ребра, соединяющего вершины
, так как в графе нет ребра, соединяющего вершины  . И т. д.
. И т. д.


