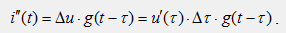Лекции по ТОЭ/ №19 Расчет переходных процессов методом интеграла Дюамеля.

Метод интеграла Дюамеля применяется для расчета переходных процессов в электрических цепях в том случае, если в рассматриваемой цепи действует источник ЭДС u(t) произвольной формы, отличной от стандартной (постоянной или синусоидальной).

Пусть к источнику ЭДС произвольной формы u(t) подключается цепь с нулевыми начальными условиями и с заданной переходной проводимостью.

Заменим непрерывную кривую ЭДС u(t) приближенно ступенчатой с интервалами по оси t между отдельными скачками, равными Δτ. Первый скачок ЭДС равен u(0) и действует в момент t=0. Все последующие скачки ЭДС можно определить как Δu=Δτ·tgα=e`(τ)Δτ и действуют они с запаздыванием на τ, то есть в момент t-τ. Ток на выходе цепи в произвольный момент времени t можно рассматривать в соответствии с принципом наложения как сумму частичных токов, возникающих под действием отдельных скачков ЭДС, следующих друг за другом через промежутки Δτ в интервале времени от 0 до t.

Частичный ток, вызванный первым источником ЭДС, будет равен i`(t)=u(0)·g(t), а частичные токи, вызванные последующими скачками ЭДС, будут равны:

Результирующий ток равен сумме частичных токов:

Перейдем к бесконечно малым интервалам Δτ→dτ и заменим сумму интегралом:

Полученное выражение для i(t) носит название интеграла Дюамеля и применяется на практике для расчета переходных процессов в электрических цепях при воздействии на них источников ЭДС или тока произвольной формы.

Порядок применения интеграла Дюамеля:

1) Выполняют расчет переходного процесса классическим или операторным методом при включении исследуемой цепи к источнику единичной постоянной ЭДС E=1 и таким образом определяют необходимую переходную функцию по току g(t) или по напряжению k(t).

2) Определяют переходную функцию g(t-τ) или k(t-τ) путем замены в выражениях g(t) или k(t) переменной t на t-τ.

3) Находят производную от функции ЭДС u`(t)=d[u(t)]/dt и в полученном выражении заменяют переменную t на τ, в результате получают функцию e`(τ).

4) Выражения функций u`(τ), g(t-τ) или k(t-τ) подставляют в формулу интеграла Дюамеля, выполняют интегрирование по переменной τ и подставляют пределы интегрирования по переменной t. При необходимости упрощают структуру полученного выражения искомой функции i(t) или u(t).

Замечания:

1) Если функция u(t) претерпевает скачки или разрывы, то она разбивается на отдельные участки с плавным изменением функции, при этом интеграл Дюамеля применяется к каждому участку в отдельности.

2) При расчете переходных процессов в цепях постоянного или синусоидального тока метод интеграла Дюамеля проигрывает классическому и операторному методам, поэтому для таких цепей он не применяется.

Пример. Рассчитать ток i(t) в цепи R, C при действии на нее трапециевидного импульса с заданными параметрами (рис. 72.2):

Переходная проводимость схемы:

Производная от функции ЭДС u(t): u`(t)=-k; u`(τ)=-k.

Так как функция u(t) в момент времени t=t₁ изменяется скачком, то ее разбиваем на два участка (0...t₁, t₁...∞), для каждого из которых находим свое решение для искомой функции i(t).