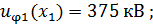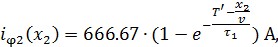Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет переходных процессов в нагрузке П2 линии 2Содержание книги
Поиск на нашем сайте Схема замещения для расчета переходного процесса:
где
Отсчет времени t " ведется от момента прихода волны ϕ2 к входным зажимам нагрузки П2 2'-2'. В этот момент времени возникает отраженная волна в линии 2. На приведенной схеме
А. Расчет операторным методом Операторное изображение напряжения
Входное операторное сопротивление цепи:
Операторное изображение входного тока в нагрузке:
Корни полинома знаменателя равны Производная знаменателя:
Таким образом,
Коэффициенты, входящие в выражение
В результате получим:
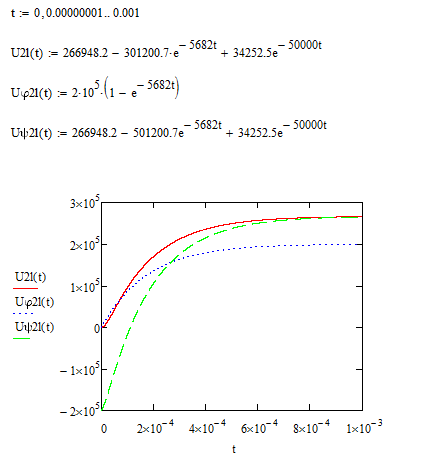
Напряжение на входе нагрузки П2 равно:
Б. Расчет входного тока нагрузки П2 в переходном процессе с помощью интеграла Дюамеля Для расчета входного тока нагрузки линии 2 применим интеграл Дюамеля в форме
Получим выражения для отдельных составляющих, входящих в интеграл Дюамеля. Учтем, что u 2(0) = 0. Для определения переходной характеристики y (t ") рассмотрим переходный процесс включения рассматриваемой цепи при нулевых начальных условиях под действие постоянного напряжения U 0=const:
Ток
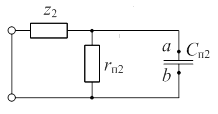
Эквивалентная схема для определения i 2 l (+0) имеет вид:
Ток i 2 l (+0) равен
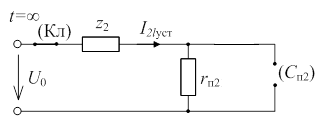
Определим i 2 l уст = i 2 l (∞). Расчётная схема при t →∞:
Постоянная времени цепи τ2:
где R экв ab – сопротивление цепи по отношению к зажимам ab конденсатора при исключенном источнике ЭДС:
Итак,
По определению
Заменив в последнем выражении время t на t ":
и далее t " на t "– x, получим:
где t " – момент времени, в который требуется определить значение искомого тока; x – время включения очередного скачка напряжения, на которые разбивается входной сигнал в интеграле Дюамеля. Найдем производную входного напряжения Так как
Подставим полученные составляющие в интеграл Дюамеля:
Обозначим: Окончательно получим
Что с точностью до погрешности округления совпадает с найденным выше результатом:
Определение напряжения и тока отраженной от нагрузки П2 волны (ψ2 l на зажимах 2' – 2')
Ток отраженной волны:
Расчет переходных процессов в нагрузке П3 линии 3
Схема замещения для расчета переходного процесса: Здесь Волновое сопротивление линии 3 принято равным z 3 = Z 3 = 300Ом. Сопротивление нагрузки: r п3 = 100 Ом. Отсчет времени t ′′′ ведется с момента прихода волны φ3 к зажимам 3'-3' нагрузки П3. Из схемы получим:
Отраженные от нагрузки П3 волны (ψ3 l на зажимах 3'-3'):
Сведем основные полученные результаты в таблицу:
Нахождение распределения напряжения и тока вдоль линий В момент времени, когда отраженная от нагрузки П2 волна пройдет расстояние s Распределение падающих и отраженных составляющих волн вдоль линий в заданный момент времени t р, когда отраженные от нагрузки 2-й линии волны прошли расстояние s = 40 км. Введем обозначения: x 1 – координаты точек линии 1, отсчитываемые от зажимов 1-1 вправо; x’ 1– координаты точек линии 1, отсчитываемые от зажимов 1'-1' влево; x 2, x’ 2 и x 3, x’ 3 – то же для линий 2 и 3 соответственно. В расчётный момент времени отраженные в линии 1 волны (ψ1) пройдут расстояние x’ 1max= l 2 + s = 50+40 = 90 км, а в линиях 2 и 3 –
Для получения распределения волны вдоль линии без потерь следует в её выражении для места возникновения заменить время t величиной
Линия 1
Линия 2
Линия 3
Заключение
В результате курсовой работы были получены характеристики системы линий и проведен расчет для установившегося синусоидального режима. Для упрощения расчетов каждая линия была заменена Т-образной схемой. В результате расчета напряжений были подобраны характеристики третьей лини. Произведены расчеты для переходных процессов в линиях. При расчете использовались такие методы, как: операторный метод, интеграл Дюамеля. Результаты, полученные с помощью обоих методов оказались равны при округление до целой величины. В результате были получены значения напряжения и тока для падающих и отраженных волн, как функции координат. При выполнение курсовой работы поставленная цель была выполнена. Библиографический список 1. Положение по содержанию, оформлению, организации выполнения и защиты курсовых проектов и курсовых работ. Приказ СПбГПУ № 583 от 01.07.2013 г. 2. К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. Теоретические основы электротехники, т. 2, 4-е издание. «Питер», 2003. Параграфы 17.1-17.8, 18.1-18.10. 3. А.Б. Новгородцев. Теоретические основы электротехники. 30 лекций по теории электрических цепей, 2-е издание. «Питер», 2006. Лекции 25, 26. 4. Н.В. Коровкин, Е.Е. Селина, В.Л. Чечурин. Теоретические основы электротехники. Сборник задач. «Питер», 2004. Разделы 16, 17. 5. Практикум по ТОЭ, ч. 2 / под ред. д.т.н. М.А. Шакирова. СПб, изд-во СПбГПУ, 2004. Тема 12. 6. Е.Ю. Кочеткова, В.С. Лопатин, М.А. Миэринь, А.Н. Модулина, А.Б. Новгородцев. Типовые задачи по теории электрических цепей, 2-е издание / под ред. проф. А.Б. Новгородцева. СПб, изд. СПбГПУ, 2004. 7. А.Б. Новгородцев. Расчет электрических цепей в МАТLАB. Учебный курс. «Питер», 2004. 8. Е.Г. Макаров. Инженерные расчеты в Mathcad. Учебный курс. «Питер», 2005.
Приложение
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.211.169 (0.01 с.) |



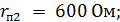



 :
:


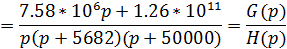




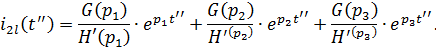




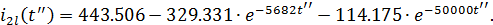
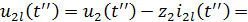
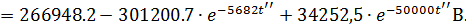




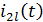







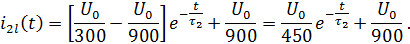



 .
.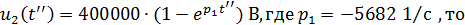


 .
.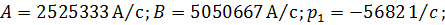
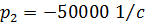 .
.
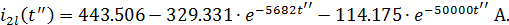

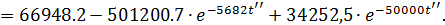
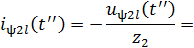








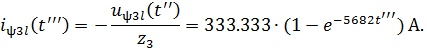




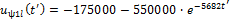
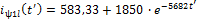
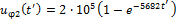




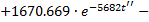



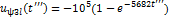



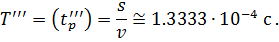
 для падающих волн
для падающих волн  и для отраженных и положить t равным расчетному времени T = t р
и для отраженных и положить t равным расчетному времени T = t р