
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические гипотезы. Проверка гипотез. Критерий Пирсона.Содержание книги
Поиск на нашем сайте
В технике, экономике, технологии и других прикладных отраслях для принятия того или иного решения часто прибегают к результатам статистических наблюдений. Статистическая гипотеза – всякое высказывание о генеральной совокупности, проверяемое по выборке. Статистические гипотезы можно разделить на два основных класса: гипотезы о законах распределения; гипотезы о параметрах распределения. Пример: Гипотеза о том, что производительность труда рабочих выполняющих одинаковую работу имеет нормальный закон распределения, является гипотезой о законе распределения. Высказывание о том, что средний рост студентов сидящих в аудитории равный некоторому числу есть гипотеза о параметрах распределения. Сформулируем в общем, виде задачу статистической проверки гипотезы о параметрах распределения. Пусть Множество допустимых значений – множество выборок O. Критическая область – множество выборок W. Так как оба множества не пересекаемые, то достаточно определить одно из этих множеств. При выборе критической области следует иметь в виду что, принимая или отвергая гипотезу, мы можем получить ошибки двух видов: 1. ошибка состоит в том, что нулевая гипотеза 2. ошибка состоит в том, что принимается гипотеза, Критерий проверки гипотезы (критерий согласия) - правило, по которому рассматриваема гипотеза, принимается или отвергается. Критерий согласия представляет собой случайную величину K, которая служит для проверки нулевой гипотезы по результатам выборки. Существует очень много критериев согласия. После выбора определенного из них множество его возможных значений разбивают на два подмножества: критическую область (те значения, при которых гипотезу отвергают) и область принятия (те значения, при которых гипотезу принимают). Таким образом, вопрос свелся к отысканию критических точек критерия, т.е таких точек которые разделяют критическую область и область принятия. С этой целью задаются уровни значимости
Существует множество всевозможных критериев согласия Фишера, Смирнова и т.д. Для этих критериев в зависимости от уровня значимости Статистические гипотезы о виде распределения делятся на простые и сложные. Простая статистическая гипотеза – гипотеза, распределенная однозначно. Сложная статистическая гипотеза – гипотеза, распределенная не однозначно. Пример: Простая статистическая гипотеза случайной величины распределена по нормальному закону распределения ( Сложная статистическая гипотеза случайной величины распределена по нормальному закону распределения с параметрами Мы с вами для примера рассмотрим только один критерий согласия: критерий Пирсона или критерий 20.
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.008 с.) |

 закон распределения случайной величины зависящий от одного параметра
закон распределения случайной величины зависящий от одного параметра  . Предположим, что нужно проверить гипотезу о том что
. Предположим, что нужно проверить гипотезу о том что  . Назовем эту гипотезу нулевой и обозначим
. Назовем эту гипотезу нулевой и обозначим  . Гипотезу о том, что
. Гипотезу о том, что  назовем конкурирующей гипотезой и обозначим
назовем конкурирующей гипотезой и обозначим 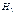 . Таким образом, перед нами стоит задача проверки гипотезы
. Таким образом, перед нами стоит задача проверки гипотезы  на основании выборки
на основании выборки  со случайной величиной X. Возможное множество выборок H можно разделить на два непересекающихся класса таких, что проверяемая гипотеза
со случайной величиной X. Возможное множество выборок H можно разделить на два непересекающихся класса таких, что проверяемая гипотеза  (
( , исходя из требования чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий примет значение из критической области, была равна
, исходя из требования чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий примет значение из критической области, была равна  . Другими словами
. Другими словами 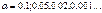
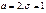 ).
). ).
).



