
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительные интервалы. Доверительная вероятность.
На практике часто требуется не только найти оценку параметра, но и оценить ее точность и надежность. Эта задача особенно актуальна при малом числе испытаний, когда замена параметра a его оценкой может привести к большим ошибкам. В математической статистике для определении точности и надежности оценки Пусть Данная вероятность – доверительная вероятность. Найдем такое 17. Доверительный интервал для оценки математического ожидания при известном Пусть количественный признак X распределен по нормальному закону распределения, причем заранее известно
Замечания: из формулы для оценки точности следует, что с увеличением n число если требуется оценить математическое ожидание с напередзаданной точностью
18. Доверительный интервал для оценки математического ожидания при неизвестном Пусть случайная величина распределена по нормальному закону распределения. Нам нужно найти доверительный интервал с надежностью j для математического ожидания. Извлекаем выборку объема n. По этой выборке находим оценку математического ожидания
где Замечание: из предельных соотношений показывается, что если 19. Схема применения критерия Пусть у нас имеется гипотеза о том, что закон распределения нормальный. делаем выборку из генеральной совокупности и по выборке составляем интервальный ряд, для чего находим интервальный ряд K; по выборке находим оценки параметров
принимаем статистическое решение. Гипотеза (k – число степеней свободы, l – число параметров). Если же
|
|||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.189.85 (0.009 с.) |
 используют доверительные интервал и вероятность.
используют доверительные интервал и вероятность. .
. что
что  . Тогда возможные ошибки будут находиться в диапазоне
. Тогда возможные ошибки будут находиться в диапазоне  . А ошибки по абсолютной величине большие
. А ошибки по абсолютной величине большие  будут встречаться крайне редко с вероятностью 1-P. Последнее неравенство запишем в развернутом виде:
будут встречаться крайне редко с вероятностью 1-P. Последнее неравенство запишем в развернутом виде:  . Это равенство означает, что с вероятностью P истинное значение параметра находится в интервале
. Это равенство означает, что с вероятностью P истинное значение параметра находится в интервале  (доверительный интервал).
(доверительный интервал). .
. . Нам требуется оценить неизвестное математическое ожидание
. Нам требуется оценить неизвестное математическое ожидание  по выборочной средней
по выборочной средней  . Другими словами построить доверительный интервал для математического ожидания. Будем рассматривать оценки
. Другими словами построить доверительный интервал для математического ожидания. Будем рассматривать оценки  будет изменяться от выборки к выборке. Доказано что математическое ожидание
будет изменяться от выборки к выборке. Доказано что математическое ожидание  . А
. А 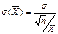 , где n – объем выборки. Поскольку X имеет нормальное распределение то вероятность отклонения
, где n – объем выборки. Поскольку X имеет нормальное распределение то вероятность отклонения  , где
, где  . И пусть задана доверительная вероятность
. И пусть задана доверительная вероятность 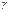 . Из соотношения
. Из соотношения  мы получаем что
мы получаем что  . По таблице значений функции Лапласа мы находим
. По таблице значений функции Лапласа мы находим  . И тогда из соотношения
. И тогда из соотношения  мы находим, что
мы находим, что  и искомый доверительный интервал будет:
и искомый доверительный интервал будет:
 убывает и, следовательно, точность оценки возрастает;
убывает и, следовательно, точность оценки возрастает; и надежностью,
и надежностью,  то минимальный объем выборки:
то минимальный объем выборки: 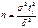 .
.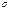 .
. и оценку среднеквадратического отклонения (несмещенного)
и оценку среднеквадратического отклонения (несмещенного)  . Тогда доверительный интервал имеет следующий вид:
. Тогда доверительный интервал имеет следующий вид:
 находится из соотношения
находится из соотношения  по таблицам распределения Стьюдента. Здесь таблицы заданы по двум параметрам. В таблицу входит кроме j еще и n-число степеней свободы.
по таблицам распределения Стьюдента. Здесь таблицы заданы по двум параметрам. В таблицу входит кроме j еще и n-число степеней свободы. то распределение Стьюдента стремиться к нормальному распределению. Поэтому когда n>30 то вместо распределения Стьюдента пользуются нормальным распределением, однако когда n<30, то замена распределения Стьюдента нормальным распределением может привести к значительным ошибкам.
то распределение Стьюдента стремиться к нормальному распределению. Поэтому когда n>30 то вместо распределения Стьюдента пользуются нормальным распределением, однако когда n<30, то замена распределения Стьюдента нормальным распределением может привести к значительным ошибкам.
 ; записываем закон распределения (нормальный) с найденными оценками (в качестве параметров; по найденному закону распределения находим вероятности
; записываем закон распределения (нормальный) с найденными оценками (в качестве параметров; по найденному закону распределения находим вероятности  попадания в каждый интервал; вычисляем
попадания в каждый интервал; вычисляем  , где
, где  - частота попадания в I-ай интервал;
- частота попадания в I-ай интервал; о том, что закон распределения нормальный не противоречит выборке наблюдений при заданном уровне значимости
о том, что закон распределения нормальный не противоречит выборке наблюдений при заданном уровне значимости  , если
, если  , где
, где 
 , то гипотеза отвергается. Для определения
, то гипотеза отвергается. Для определения 


