
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы корреляционного анализа.Содержание книги
Поиск на нашем сайте
Во многих задачах приходится установить зависимость между двумя или несколькими случайными величинами. Эта зависимость может быть функциональной или статистической. Функциональная зависимость – зависимость, при которой одному значению X ставится строго соответственное значение Y. Статистическая зависимость – зависимость, при которой изменение одной из величин влечет за собой изменение и другой случайной величины. Для определения статистической зависимости данные записывают в виде таблицы.
Фактически первый и последний столбцы представляют собой ряд распределения для составляющей X, а первая и последняя строки – ряд распределения для составляющей Y. По корреляционной таблице строят условную среднюю. Условное среднее Таким образом, мы можем составить ряд условных распределений.
Совершенно аналогично мы можем составить условное распределение Корреляционная зависимость Y от X – зависимость условной средней Корреляционная зависимость X от Y – зависимость условной средней Уравнение Уравнение В теории корреляции рассматриваются две основные задачи: 1.установить вид корреляционной зависимости; 2.определить саму функциональную зависимость и ее тесноту. Линейная корреляционная зависимость, если корреляционные зависимости
Дифференцировав функцию и приравняв к 0, мы получили следующую систему для определения параметров a и b.
Или преобразовав данную систему, мы можем записать:
Решая данную систему, мы получим:
И тогда уравнение линейной регрессии имеет вид:
Совершенно аналогично получается
Из уравнений Рассмотрим сейчас коэффициент корреляции, который был введен в теории вероятностей.
Мы знаем что
Аналогично Тогда уравнение линейной регрессии имеет вид:
Из уравнения регрессии возникает следующее: 1. точка пересечения линий регрессии –
2. если r=0, то линейная зависимость отсутствует; 3. Чем ближе Замечание: если r=0, то линейная зависимость отсутствует, но может быть нелинейная корреляционная зависимость.
22. ЛИНЕЙНОЕ ПРОГРАМИРОВАНИЕ
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.244 (0.006 с.) |

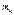 означает что
означает что 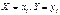 .
. означает, что
означает, что 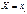 наблюдалось
наблюдалось  раз
раз означает, что
означает, что  наблюдалось
наблюдалось 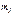 раз
раз - среднее арифметическое значение случайной величины Y, когда X приняло значение x.
- среднее арифметическое значение случайной величины Y, когда X приняло значение x.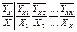
 .
.

 - уравнение регрессии Y на X, а f(x) – регрессия Y на X.
- уравнение регрессии Y на X, а f(x) – регрессия Y на X. – регрессия X на Y.
– регрессия X на Y. и
и  линейные функции.
линейные функции. Пусть у нас задано распределение условной средней
Пусть у нас задано распределение условной средней  . На плоскости
. На плоскости 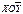 наносим. По расположению точек мы определяем вид функциональной зависимости. Для простоты будем считать, что функциональная зависимость носит линейный характер, т.е
наносим. По расположению точек мы определяем вид функциональной зависимости. Для простоты будем считать, что функциональная зависимость носит линейный характер, т.е . Тогда в каждой из точек
. Тогда в каждой из точек 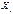 мы находим отклонение
мы находим отклонение  . Суммируем эти отклонения. Поскольку отклонения бывают разных знаков, то они будут друг друга уничтожать. Для учета отклонений мы будем брать их в квадрате.
. Суммируем эти отклонения. Поскольку отклонения бывают разных знаков, то они будут друг друга уничтожать. Для учета отклонений мы будем брать их в квадрате. . Параметры a и b мы будем выбирать из условия минимума суммы квадратов отклонений, т.е. по методу МНК. Для чего мы должны решить задачу на экстремум:
. Параметры a и b мы будем выбирать из условия минимума суммы квадратов отклонений, т.е. по методу МНК. Для чего мы должны решить задачу на экстремум: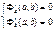
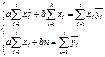
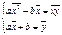
 -угловой коэффициент прямой регрессии Y на X/
-угловой коэффициент прямой регрессии Y на X/


 и
и  мы видим, что
мы видим, что  и
и  имеют одинаковый знак, совпадающий со знаком выражения.
имеют одинаковый знак, совпадающий со знаком выражения. - первый смешанный момент
- первый смешанный момент . Откуда
. Откуда
 .
.
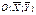 ;
;

 к 1, тем теснее линейная зависимость. На практике считают, что если r>0.6, то между случайными величинам существует сильная линейная зависимость.
к 1, тем теснее линейная зависимость. На практике считают, что если r>0.6, то между случайными величинам существует сильная линейная зависимость.


