
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое определение вероятростей.Стр 1 из 12Следующая ⇒
Классическое определение вероятростей. Всякая наука содержит ряд основных понятий, на которых она базируется. Так в физике – сила, масса, скорость; в геометрии – точка луч, а в теории вероятностей – события. Событие – любой факт, который может произойти в результате эксперимента. Все события можно разделить на три основных типа: достоверное событие – если оно обязательно происходят в результате эксперимента. Достоверные события мы будем обозначать Непосредственный подсчет вероятностей. Рассмотрим три случайных события: А – выпадение решки при одном бросании монеты; B – выпадение трех решек при трехкратном бросании монеты; C - выпадение хотя бы одной решки при трехкратном бросании монеты. Для того чтобы сравнивать события по вероятности нам нужно ввести единицу измерения. Поскольку невозможное событие никогда не произойдет, то, естественно, вероятность его появления равна 0, а у достоверного события вероятность равна 1 тогда вероятность случайного события Вероятность – численная мера степени объективной возможности случайного события. Если мы рассмотрим случайное одиночное событие, то мы ничего определенного сказать не сможем. Другое дело, когда мы рассматриваем множество однородных случайных событий. Теория вероятностей занимается изучением однородных случайных массовых событий. Рассмотрим классификацию случайных событий: 1) полная группа событий – если в результате опыта произойдет хотя бы одно из них; 2) несовместимые события – если никакие два из них не могут появиться одновременно. противоположные события – два несовместных события образующих полную группу ( Равновозможные события – если по условиям опыта есть основание считать что ни одно из этих событий не является объективно более возможным, чем другие. Элементарные события (случаи) – события образующие полную группу несовместных, равновозможных событий. Множество всех элементарных событий образует пространство элементарных событий и обозначается обычно Случай или элементарное событие – благоприятствующее событию Классическое определение вероятности.
Вероятность события A - отношение благоприятных для этого события случаев к общему числу случаев.
Статистическая вероятность Классическое определение вероятности применимо к опытам, которые сводятся к схеме случаев. Однако не всякий опыт может быть сведен к схеме случаев. . В этом случае для определения вероятности прибегают к статистическим методам. Пусть проведена серия из n опытов и событие A появилось в этой серии m раз. Тогда частота события Это свойство устойчивости частоты подтверждается многочисленными опытами и является одной из закономерностей свойственных случайным явлениям. Понятие частоты и вероятности тесно связаны между собой. Характеризуя событие вероятностью, мы не можем представить этим числом ни что иное, как частоту появления этого события. 2. Теорема умножения. Событие A зависимое от события B, если его вероятность зависит от того, произошло ли событие B. Условная вероятность – вероятность появления события A при условии, что произошло событие B.
Основные свойства условной вероятности: Если событие A зависит (не зависит) от события B, то и событие B зависит (не зависит) от события A. Если события A и B независимы, то независимы Если события A и B независимы, то вероятность
Теорема: Вероятность произведения двух зависимых событий равна вероятности первого события умноженной на вероятность второго события, при условии, что первое произошло.
Доказательство: Доказательство приведем для двух событий, сводящихся к схеме случая. Пусть у нас имеется n элементарных исходов. Из них m - благоприятных событию A, L – событию B, k – их совместному появлению.
Замечание: теорема обобщается на случай произвольного числа событий.
Теорема: Вероятность произведения двух независимых событий равна произведению их вероятностей.
Независимые в совокупности события – несколько событий, вероятность которых не зависит от того какова совокупность других событий. Следствие: вероятность произведения независимых в совокупности событий равна произведению их вероятностей. 1) 2) Если события
Совместные события – события, появление одного и которых не исключает появления другого. Схема Бернулли. Пусть производится серия из n испытаний, причем в каждом из испытаний событие A может появиться с постоянной вероятностью P и не появиться с вероятностью Теорема: формула Бернулли. Вероятность того, что в серии из n опытов событие A появится k раз, вычисляется по формуле Вывод формулы Бернулли. Вероятность одного сложного события состоит в том, что в серии n из испытаний событие A появится, раз и не появится n-k равно Пример: Пусть проводится серия из 4 испытаний. Причем будем рассматривать событие, когда A появляется три раза. Таких событий будет:
Формулой Бернулли удобно пользоваться в тех случаях, когда число испытаний небольшое. Если же число испытаний большое, то в этих случаях пользуются формулами Лапласа и Пуассона. 6. Формула Пуассона. В случае если в схеме Бернулли число испытаний большое, а вероятность стремиться к 0, то в этом случае пользуются формулой Пуассона:
где 7. Математические ожидания. Математическое ожидание случайной величины – сумма произведений всех ее возможных значений на их вероятности.
Вероятностный смысл математического ожидания состоит в том, что оно приближенно равно среднему ожидаемому значению случайной величины. Доказательство: Пусть для случайной величины проверена серия из K испытаний, причем
где А мы знаем, что если Рассмотрим
Произведение данных случайных величин
Арифметическая сумма
Произведение случайной величины X на C=const – величина
Две случайные величины независимы, если закон распределения одной не зависит от того, какое значение приняла другая. Свойства математического ожидания: 1. 2. 3. 4. 5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно 0. Замечание: от любого случайного события, каково бы оно не было, всегда можно перейти к случайной величине. Пусть A – случайное событие, которое может произойти или не произойти. Поставим ему в соответствие случайную величину X, причем X=0, если случайное событие произойдет. 10. 11. Равномерное распределение В некоторых задачах в практике встречаются случайные величины все значения, которых: a) принадлежат промежутку [a; b] б) возможные значения одинаково вероятны О таких случайных величинах говорят, что они имеют равномерное распределение. Пример: Шкала измерительного прибора проградуирована. Ошибка, которая будет допускаться при округлении: [0; 05]
Для непрерывной случайной величины: 1) Функция плотности f(x) имеет вид:
Найдем значения параметра b из условий нормировки.
Тогда:
3) Интегральная функция распределения
Рассмотрим по промежуткам: а)
б)
в)
3) Математическое ожидание
Аналогично получаем:
4) Вероятность попадания в заданный интервал:
Показательное распределение 1) Дифференциальная функция плотности показательного распределения имеет вид:
График этой функции представлен на рисунке.
2)
3)
4) Вывод: действительно 12. 13. 13. 13. 13. 14. 15. Основные понятия МАТЕМАТИЧЕСКой СТАТИСТИКи Математическая статистика – наука, занимающаяся установление закономерностей которым подчинены массовые однородные случайные явления. Перед математической статистикой стоят две задачи: правильно указать способы сбора информации; правильно указать способы анализа и обработки информации. Основные понятия математической статистики Пусть требуется изучить совокупность N однородных объектов относительно некоторого признака. Можно поступить двояко: произвести сплошное обследование (обследовать каждый объект относительно этого признака) или мы можем взять некоторую часть объектов, исследовать их и полученные результаты распространить на всю совокупность. Выборка – обследуемые объекты. Генеральная совокупность - вся совокупность объектов.. Объем выборки – число объектов в выборке. Существуют разные виды выборки: повторная, если объект после исследования возвращается в генеральную совокупность. не повторная, если объект не возвращается в генеральную совокупность. На практике, как правило, пользуются бесповторной выборкой. Выборка должна достаточно объективно отражать все особенности исследуемых объектов. Способы отбора. Простой случайный отбор – объекты извлекаются по одному из всей генеральной совокупности. Осуществить такой отбор можно пользуясь таблицами или датчиками случайных чисел. Типический отбор – объекты отбирают не из всей генеральной совокупность, а из некоторой ее части. Пример: Изделия изготавливают на нескольких станках, а проверяют изделия с одного станка.
Серийный отбор – объекты отбирают из генеральной совокупности сериями (пачками). Пример: Выпускают лампочки и проверяют сразу ящик. Статистический ряд. Пусть из генеральной совокупности извлечена выборка объема n, причем значение
Обычно эти значения располагают в порядке возрастания и записывают в виде таблицы. - значение вариантов - частоты - относительные частоты
Размах выборки – разность Такой рая – статистический вариационный ряд. Однако если объем выборки очень большой, то в этом случае вместо статистического ряда составляют интервальный статистический ряд. Для этого всю выборку разбивают на K интервалов при помощи формулы
Наряду с интервальным рядом пользуются расширенным интервальным рядом.
Полигон и гистограмма. В целях наглядности строят различные графики статистического распределения. Полигон частот – ломанная, отрезки, которой соединяют точки
Полигон относительных частот – ломанная, отрезки, которой соединяют точки Если же выборка задана интервальным рядом распределения, тогда строят гистограмму. Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников основаниями которых являются длины интервалов, а высота равна Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников основаниями которых являются длины интервалов, а высота равна На практике чаще всего строят гистограмму относительных частот. Пример:
16. Статистические оценки параметров распределения. Пусть требуется изучить некоторый признак генеральной совокупности. И пусть мы каким-то образом установили закон распределения. Нам надо найти параметры данного закона распределения. Например, если закон распределения нормальный то нам надо найти a и Любое распределение имеет свои параметры. Пусть закон распределения будет f(a; x). Поскольку мы точно не знаем параметр, то мы можем найти его по выборке. Оценка – любое значение параметра найденное по выборке. Оценка обозначается состоятельность Оценка состоятельная, если при увеличении числа опытов оценка по вероятности стремится к истинному значению. не смещенность Оценка не смещенная, если при пользовании ей не ошибок одно знака. эффективность Оценка эффективная, если по сравнению с другими оценками она имеет наименьшую дисперсию. Точечные оценки параметров распределения. Точечная оценка – оценка, выраженная одним числом. Интервальная оценка – оценка, заданная интервалом. Пусть задан ряд распределения.
Статистическое среднее (оценка математического ожидания) - Если у нас ряд распределения интервальный то
Замечание: если первоначальные варианты Тогда Доказано что оценка математического ожидания является состоятельной и несмещенной. Теория вероятности в качестве меры рассеивания случайной величины рассматривает дисперсию. В статистике рассматривают оценку дисперсии или выборочную дисперсию (вычисляется по формуле Если же ряд задан интервально то
Замечание: если значения
В математической статистик доказывается, что дисперсия является состоятельной оценкой, но смещенной. Причем несмещенная дисперсия связана со смещенной следующим соотношением: Оценка среднеквадратического отклонения - Замечание: на практике когда . 17. Доверительный интервал для оценки математического ожидания при известном Пусть количественный признак X распределен по нормальному закону распределения, причем заранее известно
Замечания: из формулы для оценки точности следует, что с увеличением n число если требуется оценить математическое ожидание с напередзаданной точностью
18. Доверительный интервал для оценки математического ожидания при неизвестном Пусть случайная величина распределена по нормальному закону распределения. Нам нужно найти доверительный интервал с надежностью j для математического ожидания. Извлекаем выборку объема n. По этой выборке находим оценку математического ожидания
где Замечание: из предельных соотношений показывается, что если 19. Схема применения критерия Пусть у нас имеется гипотеза о том, что закон распределения нормальный. делаем выборку из генеральной совокупности и по выборке составляем интервальный ряд, для чего находим интервальный ряд K; по выборке находим оценки параметров
принимаем статистическое решение. Гипотеза (k – число степеней свободы, l – число параметров). Если же 20. 22. ЛИНЕЙНОЕ ПРОГРАМИРОВАНИЕ Задача оптимального раскроя Рассмотрим следующую задачу. Пусть у нас имеются бревна длиной L(м) и нам требуется раскряжевать эти бревна на заготовки длиной Все исходные данные запишем в виде таблицы. Обозначим через
При этом мы должны выполнить план по количеству заготовок
Здесь математическая модель представляет собой нахождение минимума функции (3) при линейных ограничениях (4), причем ограничения заданы в виде строгого равенства. 23. 24. 25. Симплекс метод Когда число переменных больше двух, то графический метод не работает, и переходят к другим аналитическим методам решения. Одним из основных аналитических методов решения задач линейного программирования является симплекс метод. Свое название он получил от латинского слова “простой”. Теория и алгоритм симплекс метода строятся для канонической формы задач линейного программирования. Как вытекает из графического метода решения задачи линейного программирования, оптимальное решение находится среди крайних точек (вершин) многоугольника допустимых решений. В общем случае, когда число переменных больше двух ограничения задают некоторую многогранную область. Известно, что экстремум (решение задачи линейного программирования) линейная функция достигает среди крайних точек этого многогранника. Это решение можно найти путем перебора всех этих крайних точек. Однако из-за большого числа вычислений такой путь практически невозможен. В симплекс методе используется целенаправленный перебор, когда переход от одной вершины в соседнюю происходит в направлении скорейшего возрастания целевой функции, поэтому при решении задачи линейного программирования симплекс методом выделяются следующие три этапа: отыскание какой-либо крайней точки; проверка оптимальности; указание процедуры целенаправленного перехода к следующей крайней точке. В этом состоит эвалистическое обоснование симплекс метода. Рассмотрим основные понятия симплекс метода. Пусть задача линейного программирования задана в канонической форме: План задачи линейного программирования – вектор, Базисный план Невырожденный базисный план – базисный план, содержащий ровно m ненулевых компонентов. Оптимальный план задачи линейного программирования – план, составляющий максимальное значение целевой функции.
25 Первый этап: построение первоначального базисного плана. Пусть задача линейного программирования задана в канонической форме, причем среди векторов
Другими словами матрица условий имеет вид:
Полагая, что в системе (4) 25 27. Транспортная задача.
Для некоторых видов задач линейного программирования существуют методы, значительно упрощающие решение по сравнению с симплекс методом. Одной из таких задач является транспортная задача. Пусть имеется m предприятий Математическая модель данной задачи будет следующая. Исследуем на минимум целевую функцию:
Кроме того, мы будем предполагать, что выполняется условие баланса, т.е. Стоимость перевозок от производителя к потребителям записывают в виде матрицы тарифов.
Матрица перевозок – план транспортной задачи.
Процесс решения транспортной задачи состоит из трех основных этапов: построение первоначального допустимого плана; Допустимый план – план, удовлетворяющий ограничениям (2) и (3) проверка допустимого плана на оптимальность; в случае неоптимальности указать процедуру перехода к новому допустимому плану 28. Основные понятия теории массового обслуживания Потоки событий Одним из основных понятий теории массового обслуживания является понятие потока событий. Поток событий – последовательность однородных событий, появляющихся одно за другим в случайные моменты времени. Примеры: Поток автопоездов подвозящих древесину на нижний склад; поток отказов того или иного узла. Различают потоки однородных и неоднородных событий. Примеры: 1.поток машин прибывающих на заправку будет однородным, если мы не будем делить их на грузовые и легковые. 2.поток машин прибывающих на заправку будет неоднородным, если мы будем делить их на грузовые и легковые. Следует отметить, что термин событие в понятии поток событий отличен от понятия событие в теории вероятностей. В теории вероятностей под случайным событием понимают любой факт, который может произойти или не произойти при выполнении определенного комплекса условий. В потоке событий нет смысла говорить о вероятности события потока. Бессмысленно говорить о вероятности прибытия лесовоза на нижний склад (рано или поздно он появится). С потоком событий можно связывать различные случайные величины. Пример: Событие А – в течение времени
| Поделиться:
| |


 , где P - вероятность.
, где P - вероятность. и
и  ).
). , а сами события -
, а сами события -  .
. , если его осуществление влечет за собой появление события
, если его осуществление влечет за собой появление события  .
.
 - число благоприятствующих случаев.
- число благоприятствующих случаев. . Частота событий изменяется от серии опытов к серии. Однако если число испытаний увеличивать то частота события стабилизируется и устремится к некоторой постоянной величине – вероятности события, т.е. вероятность события, есть предел частоты
. Частота событий изменяется от серии опытов к серии. Однако если число испытаний увеличивать то частота события стабилизируется и устремится к некоторой постоянной величине – вероятности события, т.е. вероятность события, есть предел частоты  .
.
 и
и  ,
, 







 независимые в совокупности, то вероятность появления хотя бы одного из этих событий равна:
независимые в совокупности, то вероятность появления хотя бы одного из этих событий равна:
 . В этом случае говорят, что у нас действует схема Бернулли.
. В этом случае говорят, что у нас действует схема Бернулли.
 . Таких сложных несовместных событий будет столько, сколько можно сделать сочетаний из n элементов по k равно
. Таких сложных несовместных событий будет столько, сколько можно сделать сочетаний из n элементов по k равно  . Отсюда вытекает формула.
. Отсюда вытекает формула. .
.

 .
.
 появилось
появилось  раз,
раз,  . Среднее арифметическое наблюдаемое значение:
. Среднее арифметическое наблюдаемое значение:
 ,
,  то. В результате чего мы получаем
то. В результате чего мы получаем 

 и
и 
 - случайная величина.
- случайная величина.
 - случайная величина.
- случайная величина.
 , со следующим законом распределения:
, со следующим законом распределения:


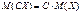 ,
, 
 , X и Y – независимые случайные величины.
, X и Y – независимые случайные величины.


 - дифференциальная функция распределения
- дифференциальная функция распределения
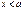

















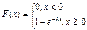





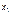 наблюдалось
наблюдалось  раз,
раз, 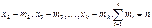 . Значения
. Значения 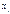 - варианты.
- варианты.

 . Составляют интервалы:
. Составляют интервалы:


 - число – вариант X значений, которые попали в i-ый интервал.
- число – вариант X значений, которые попали в i-ый интервал.
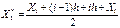
 .
.
 .
. , где h – длина интервала.
, где h – длина интервала. .
.
 , если закон показательный то -
, если закон показательный то -  .
. или
или  . Для того чтобы оценки давали хорошие результаты к ним предъявляются следующие требования:
. Для того чтобы оценки давали хорошие результаты к ним предъявляются следующие требования:


 , где
, где  - середина соответствующего интервала.
- середина соответствующего интервала. - большие числа, то для упрощения расчетов целесообразно из каждого из вариантов вычесть одно и то же число C:
- большие числа, то для упрощения расчетов целесообразно из каждого из вариантов вычесть одно и то же число C:  .
. .
. ).
). . Однако на практике пользуются другими формулами:
. Однако на практике пользуются другими формулами:
 - большие числа тогда переходят к условным вариантам
- большие числа тогда переходят к условным вариантам и
и  .
. .
.
 приблизительно считают что
приблизительно считают что  .
. .
. по выборочной средней
по выборочной средней  . Другими словами построить доверительный интервал для математического ожидания. Будем рассматривать оценки
. Другими словами построить доверительный интервал для математического ожидания. Будем рассматривать оценки  будет изменяться от выборки к выборке. Доказано что математическое ожидание
будет изменяться от выборки к выборке. Доказано что математическое ожидание  . А
. А 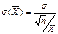 , где n – объем выборки. Поскольку X имеет нормальное распределение то вероятность отклонения
, где n – объем выборки. Поскольку X имеет нормальное распределение то вероятность отклонения  , где
, где  . И пусть задана доверительная вероятность
. И пусть задана доверительная вероятность 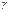 . Из соотношения
. Из соотношения  мы получаем что
мы получаем что  . По таблице значений функции Лапласа мы находим
. По таблице значений функции Лапласа мы находим  . И тогда из соотношения
. И тогда из соотношения  мы находим, что
мы находим, что  и искомый доверительный интервал будет:
и искомый доверительный интервал будет:
 убывает и, следовательно, точность оценки возрастает;
убывает и, следовательно, точность оценки возрастает; и надежностью,
и надежностью,  то минимальный объем выборки:
то минимальный объем выборки: 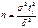 .
.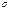 .
. и оценку среднеквадратического отклонения (несмещенного)
и оценку среднеквадратического отклонения (несмещенного)  . Тогда доверительный интервал имеет следующий вид:
. Тогда доверительный интервал имеет следующий вид:
 находится из соотношения
находится из соотношения  по таблицам распределения Стьюдента. Здесь таблицы заданы по двум параметрам. В таблицу входит кроме j еще и n-число степеней свободы.
по таблицам распределения Стьюдента. Здесь таблицы заданы по двум параметрам. В таблицу входит кроме j еще и n-число степеней свободы. то распределение Стьюдента стремиться к нормальному распределению. Поэтому когда n>30 то вместо распределения Стьюдента пользуются нормальным распределением, однако когда n<30, то замена распределения Стьюдента нормальным распределением может привести к значительным ошибкам.
то распределение Стьюдента стремиться к нормальному распределению. Поэтому когда n>30 то вместо распределения Стьюдента пользуются нормальным распределением, однако когда n<30, то замена распределения Стьюдента нормальным распределением может привести к значительным ошибкам.
 ; записываем закон распределения (нормальный) с найденными оценками (в качестве параметров; по найденному закону распределения находим вероятности
; записываем закон распределения (нормальный) с найденными оценками (в качестве параметров; по найденному закону распределения находим вероятности  попадания в каждый интервал; вычисляем
попадания в каждый интервал; вычисляем  , где
, где  - частота попадания в I-ай интервал;
- частота попадания в I-ай интервал; о том, что закон распределения нормальный не противоречит выборке наблюдений при заданном уровне значимости
о том, что закон распределения нормальный не противоречит выборке наблюдений при заданном уровне значимости  , если
, если  , где
, где 
 , то гипотеза отвергается. Для определения
, то гипотеза отвергается. Для определения  в количестве
в количестве  . Раскряжевку мы можем производить n способами. Причем при раскряжевке по j-ому способу мы получаем
. Раскряжевку мы можем производить n способами. Причем при раскряжевке по j-ому способу мы получаем  ,
,  заготовок длиной
заготовок длиной  и отходы при этом составляют
и отходы при этом составляют  . Нужно составить такой план раскряжевки, при котором заказ будет выполнен при минимальных отходах.
. Нужно составить такой план раскряжевки, при котором заказ будет выполнен при минимальных отходах. количество бревен распиленных по j-ому варианту. Тогда суммарные отходы будут равны
количество бревен распиленных по j-ому варианту. Тогда суммарные отходы будут равны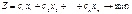 (3)
(3)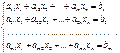 (4)
(4)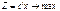 (1) при ограничениях Ax=b (2),
(1) при ограничениях Ax=b (2),  . Здесь матрица
. Здесь матрица 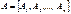 представляет собой набор векторов условий.
представляет собой набор векторов условий.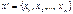 удовлетворяющий ограничениям (2).
удовлетворяющий ограничениям (2).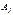 , соответствующие ненулевым компонентам, которого являются линейно независимыми.
, соответствующие ненулевым компонентам, которого являются линейно независимыми.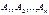 условий найдутся m линейно независимых единичных векторов, образующих единичный базис. Соответствующие им компоненты вектора x – базисные компоненты, а оставшиеся – свободные компоненты. И пусть вектор
условий найдутся m линейно независимых единичных векторов, образующих единичный базис. Соответствующие им компоненты вектора x – базисные компоненты, а оставшиеся – свободные компоненты. И пусть вектор 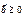 . Неограничивая общности, будем считать, что единичными базисными векторами будут первые m векторов. Тогда задача линейного программирования примет следующий вид:
. Неограничивая общности, будем считать, что единичными базисными векторами будут первые m векторов. Тогда задача линейного программирования примет следующий вид: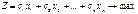 (3)
(3)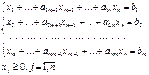 (4)
(4)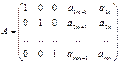
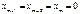 мы получим что
мы получим что 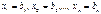 , и первоначальный базис угла будет
, и первоначальный базис угла будет 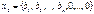 . Если же задача задана в нормальной форме, то всегда легко найти первоначальный базисный план.
. Если же задача задана в нормальной форме, то всегда легко найти первоначальный базисный план. производящих продукцию с объемами производства соответственно
производящих продукцию с объемами производства соответственно  и n предприятий
и n предприятий  потребителей этой продукции с объемами потребления
потребителей этой продукции с объемами потребления  . И пусть стоимость перевозки единицы продукции от производителя
. И пусть стоимость перевозки единицы продукции от производителя  к потребителю
к потребителю  равна
равна  . Обозначим через
. Обозначим через  количество продукции, которую будем перевозить от производителя
количество продукции, которую будем перевозить от производителя  (1)
(1) (2)
(2) (3)
(3) (4). Такая транспортная задача – закрытая транспортная задача. Если же условие баланса не выполняется, т.е.
(4). Такая транспортная задача – закрытая транспортная задача. Если же условие баланса не выполняется, т.е.  , то в этом случае вводят фиктивных потребителей или производителей, так чтобы выполнялось условие баланса.
, то в этом случае вводят фиктивных потребителей или производителей, так чтобы выполнялось условие баланса.

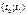 на нижний склад прибудут три лесовоза.
на нижний склад прибудут три лесовоза. Поток событий наглядно изображается на числовой оси с помощью точек
Поток событий наглядно изображается на числовой оси с помощью точек  с разделяющими их интервалами
с разделяющими их интервалами 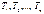 , где
, где  . Здесь
. Здесь  - момент времени, когда появилось первое событие,
- момент времени, когда появилось первое событие,  - второе событие,
- второе событие,  - n-ое событие. Потоки различают между собой по их внутренней структуре (по закону распределения интервалов
- n-ое событие. Потоки различают между собой по их внутренней структуре (по закону распределения интервалов 


